Note
Click here to download the full example code
Gradient Sensitivity¶
In this example, we illustrate the use of the GradientSensitivity
plot on the Sobieski’s SSBJ problem.
from __future__ import absolute_import, division, print_function, unicode_literals
from future import standard_library
Import¶
The first step is to import some functions from the API and a method to get the design space.
from gemseo.api import configure_logger, create_discipline, create_scenario
from gemseo.problems.sobieski.core import SobieskiProblem
configure_logger()
standard_library.install_aliases()
Create disciplines¶
Then, we instantiate the disciplines of the Sobieski’s SSBJ problem: Propulsion, Aerodynamics, Structure and Mission
disciplines = create_discipline(
[
"SobieskiPropulsion",
"SobieskiAerodynamics",
"SobieskiStructure",
"SobieskiMission",
]
)
Create design space¶
We also read the design space from the SobieskiProblem.
design_space = SobieskiProblem().read_design_space()
Create and execute scenario¶
The next step is to build a MDO scenario in order to maximize the range, encoded ‘y_4’, with respect to the design parameters, while satisfying the inequality constraints ‘g_1’, ‘g_2’ and ‘g_3’. We can use the MDF formulation, the SLSQP optimization algorithm and a maximum number of iterations equal to 100.
scenario = create_scenario(
disciplines,
formulation="MDF",
objective_name="y_4",
maximize_objective=True,
design_space=design_space,
)
scenario.set_differentiation_method("user")
for constraint in ["g_1", "g_2", "g_3"]:
scenario.add_constraint(constraint, "ineq")
scenario.execute({"algo": "SLSQP", "max_iter": 10})
Out:
{'algo': 'SLSQP', 'max_iter': 10}
Post-process scenario¶
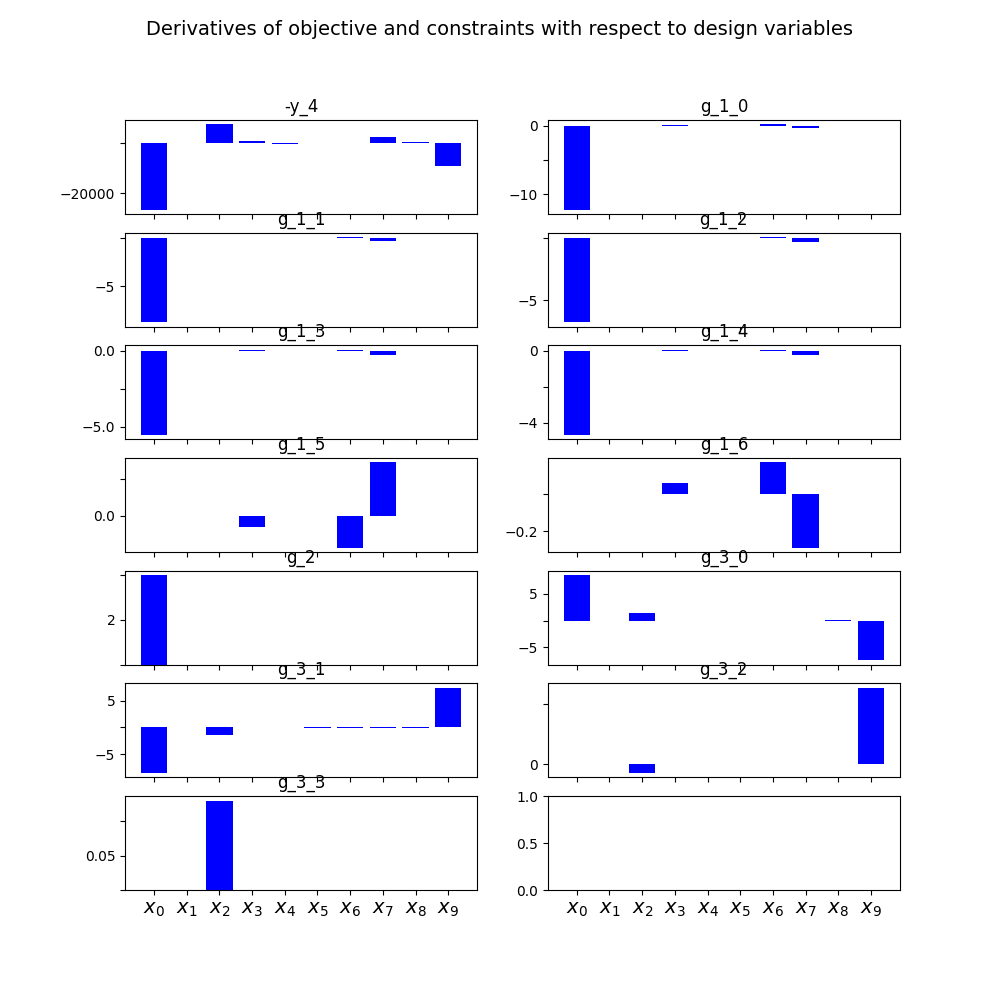
Lastly, we post-process the scenario by means of the GradientSensitivity
plot which builds histograms of derivatives of objective and constraints.
scenario.post_process("GradientSensitivity", save=False, show=True)
Out:
/home/docs/checkouts/readthedocs.org/user_builds/gemseo/conda/3.0.3/lib/python3.8/site-packages/gemseo/post/gradient_sensitivity.py:141: UserWarning: FixedFormatter should only be used together with FixedLocator
axe.set_xticklabels(x_labels, fontsize=14)
<gemseo.post.gradient_sensitivity.GradientSensitivity object at 0x7fc29db48040>
Total running time of the script: ( 0 minutes 1.227 seconds)
