design_space module¶
Design space.
A design space is used to represent the optimization’s unknowns, a.k.a. the design variables.
A DesignSpace describes this design space at a given state, in terms of names,
sizes, types, bounds and current values of the design variables.
Variables can easily be added to the DesignSpace using the
DesignSpace.add_variable() method or removed using the
DesignSpace.remove_variable() method.
We can also filter the design variables using the DesignSpace.filter() method.
Getters and setters are also available to get or set the value of a given variable property.
Lastly, an instance of DesignSpace can be stored in a txt or HDF file.
- class gemseo.algos.design_space.DesignSpace(name='')[source]¶
Bases:
MutableMappingDescription of a design space.
It defines a set of variables from their names, sizes, types and bounds.
In addition, it provides the current values of these variables that can be used as the initial solution of an
OptimizationProblem.A
DesignSpacehas the same API as a dictionary, e.g.variable = design_space["x"],other_design_space["x"] = design_space["x"],del design_space["x"],for name, value in design_space["x"].items(), …- Parameters:
name (str) –
The name to be given to the design space. If empty, the design space is unnamed.
By default it is set to “”.
- class DesignVariable(size=1, var_type=_DesignVariableType.FLOAT, l_b=None, u_b=None, value=None)[source]¶
Bases:
NamedTupleA design variable.
Create new instance of DesignVariable(size, var_type, l_b, u_b, value)
- Parameters:
size (int | None) –
By default it is set to 1.
var_type (NDArray[_DesignVariableType] | _DesignVariableType | None) –
By default it is set to “float”.
l_b (ndarray | None) –
u_b (ndarray | None) –
value (ndarray | None) –
- count(value, /)¶
Return number of occurrences of value.
- index(value, start=0, stop=9223372036854775807, /)¶
Return first index of value.
Raises ValueError if the value is not present.
- DesignVariableType¶
alias of
_DesignVariableType
- add_variable(name, size=1, var_type=_DesignVariableType.FLOAT, l_b=None, u_b=None, value=None)[source]¶
Add a variable to the design space.
- Parameters:
name (str) – The name of the variable.
size (int) –
The size of the variable.
By default it is set to 1.
var_type (DesignVariableType | Sequence[DesignVariableType]) –
Either the type of the variable or the types of its components.
By default it is set to “float”.
l_b (float | ndarray | None) – The lower bound of the variable. If
None, use \(-\infty\).u_b (float | ndarray | None) – The upper bound of the variable. If
None, use \(+\infty\).value (float | ndarray | None) – The default value of the variable. If
None, do not use a default value.
- Raises:
ValueError – Either if the variable already exists or if the size is not a positive integer.
- Return type:
None
- array_to_dict(x_array)[source]¶
Convert a design array into a dictionary indexed by the variables names.
- check()[source]¶
Check the state of the design space.
- Raises:
ValueError – If the design space is empty.
- Return type:
None
- check_membership(x_vect, variable_names=None)[source]¶
Check whether the variables satisfy the design space requirements.
- Parameters:
- Raises:
ValueError – Either if the dimension of the values vector is wrong, if the values are not specified as an array or a dictionary, if the values are outside the bounds of the variables or if the component of an integer variable is not an integer.
- Return type:
None
- clear() None. Remove all items from D.¶
- dict_to_array(design_values, variable_names=None)[source]¶
Convert a mapping of design values into a NumPy array.
- Parameters:
- Returns:
The design values as a NumPy array.
- Return type:
ndarray
Notes
The data type of the returned NumPy array is the most general data type of the values of the mapping
design_valuescorresponding to the keys iterable fromvariables_names.
- extend(other)[source]¶
Extend the design space with another design space.
- Parameters:
other (DesignSpace) – The design space to be appended to the current one.
- Return type:
None
- filter(keep_variables, copy=False)[source]¶
Filter the design space to keep a subset of variables.
- Parameters:
- Returns:
Either the filtered original design space or a copy.
- Raises:
ValueError – If the variable is not in the design space.
- Return type:
- filter_dim(variable, keep_dimensions)[source]¶
Filter the design space to keep a subset of dimensions for a variable.
- Parameters:
- Returns:
The filtered design space.
- Raises:
ValueError – If a dimension is unknown.
- Return type:
- classmethod from_csv(file_path, header=None)[source]¶
Create a design space from a CSV file.
- Parameters:
- Returns:
The design space defined in the file.
- Raises:
ValueError – If the file does not contain the minimal variables in its header.
- Return type:
- classmethod from_file(file_path, hdf_node_path='', **options)[source]¶
Create a design space from a file.
- Parameters:
file_path (str | Path) – The path to the file. If the extension starts with “hdf”, the file will be considered as an HDF file.
hdf_node_path (str) –
The path of the HDF node from which the database should be imported. If empty, the root node is considered.
By default it is set to “”.
**options (Any) – The keyword reading options.
- Returns:
The design space defined in the file.
- Return type:
- classmethod from_hdf(file_path, hdf_node_path='')[source]¶
Create a design space from an HDF file.
- Parameters:
- Returns:
The design space defined in the file.
- Return type:
- get(k[, d]) D[k] if k in D, else d. d defaults to None.¶
- get_active_bounds(x_vec=None, tol=1e-08)[source]¶
Determine which bound constraints of a design value are active.
- Parameters:
x_vec (ndarray | None) – The design value at which to check the bounds. If
None, use the current design value.tol (float) –
The tolerance of comparison of a scalar with a bound.
By default it is set to 1e-08.
- Returns:
Whether the components of the lower and upper bound constraints are active, the first returned value representing the lower bounds and the second one the upper bounds, e.g.
( { "x": array(are_x_lower_bounds_active), "y": array(are_y_lower_bounds_active), }, { "x": array(are_x_upper_bounds_active), "y": array(are_y_upper_bounds_active), }, )
where:
are_x_lower_bounds_active = [True, False] are_x_upper_bounds_active = [False, False] are_y_lower_bounds_active = [False] are_y_upper_bounds_active = [True]
- Return type:
- get_current_value(variable_names=None, complex_to_real=False, as_dict=False, normalize=False)[source]¶
Return the current design value.
If the names of the variables are empty then an empty data is returned.
- Parameters:
variable_names (Sequence[str] | None) – The names of the design variables. If
None, use all the design variables.complex_to_real (bool) –
Whether to cast complex numbers to real ones.
By default it is set to False.
as_dict (bool) –
Whether to return the current design value as a dictionary of the form
{variable_name: variable_value}.By default it is set to False.
normalize (bool) –
Whether to normalize the design values in \([0,1]\) with the bounds of the variables.
By default it is set to False.
- Returns:
The current design value.
- Raises:
ValueError – If names in
variable_namesare not in the design space.- Return type:
Warning
For performance purposes,
get_current_value()does not return a copy of the current value. This means that modifying the returned object will make theDesignSpaceinconsistent (the current design value stored as a NumPy array and the current design value stored as a dictionary of NumPy arrays will be different). To modify the returned object without impacting theDesignSpace, you shall copy this object and modify the copy.See also
To modify the current value, please use
set_current_value()orset_current_variable().
- get_indexed_var_name(variable_name)[source]¶
Create the names of the components of a variable.
If the size of the variable is equal to 1, this method returns the name of the variable. Otherwise, it concatenates the name of the variable, the separator
DesignSpace.SEPand the index of the component.
- get_indexed_variable_names()[source]¶
Create the names of the components of all the variables.
If the size of the variable is equal to 1, this method uses its name. Otherwise, it concatenates the name of the variable, the separator
DesignSpace.SEPand the index of the component.
- get_lower_bound(name)[source]¶
Return the lower bound of a variable.
- Parameters:
name (str) – The name of the variable.
- Returns:
The lower bound of the variable (possibly infinite).
- Return type:
ndarray | None
- get_lower_bounds(variable_names: Sequence[str] | None = None, as_dict: Literal[False] = False) ndarray[source]¶
- get_lower_bounds(variable_names: Sequence[str] | None = None, as_dict: Literal[True] = False) dict[str, ndarray]
Return the lower bounds of design variables.
- Parameters:
variable_names – The names of the design variables. If
None, the lower bounds of all the design variables are returned.as_dict – Whether to return the lower bounds as a dictionary of the form
{variable_name: variable_lower_bound}.
- Returns:
The lower bounds of the design variables.
- get_pretty_table(fields=None, with_index=False, capitalize=False, simplify=False)[source]¶
Build a tabular view of the design space.
- Parameters:
fields (Sequence[str] | None) – The name of the fields to be exported. If
None, export all the fields.with_index (bool) –
Whether to show index of names for arrays. This is ignored for scalars.
By default it is set to False.
capitalize (bool) –
Whether to capitalize the field names and replace
"_"by" ".By default it is set to False.
simplify (bool) –
Whether to return a simplified tabular view.
By default it is set to False.
- Returns:
A tabular view of the design space.
- Return type:
- get_upper_bound(name)[source]¶
Return the upper bound of a variable.
- Parameters:
name (str) – The name of the variable.
- Returns:
The upper bound of the variable (possibly infinite).
- Return type:
ndarray | None
- get_upper_bounds(variable_names: Sequence[str] | None = None, as_dict: Literal[False] = False) ndarray[source]¶
- get_upper_bounds(variable_names: Sequence[str] | None = None, as_dict: Literal[True] = False) dict[str, ndarray]
Return the upper bounds of design variables.
- Parameters:
variable_names – The names of the design variables. If
None, the upper bounds of all the design variables are returned.as_dict – Whether to return the upper bounds as a dictionary of the form
{variable_name: variable_upper_bound}.
- Returns:
The upper bounds of the design variables.
- get_variables_indexes(variable_names, use_design_space_order=True)[source]¶
Return the indexes of a design array corresponding to variables names.
- Parameters:
variable_names (Iterable[str]) – The names of the variables.
use_design_space_order (bool) –
Whether to order the indexes according to the order of the variables names in the design space. Otherwise the indexes will be ordered in the same order as the variables names were required.
By default it is set to True.
- Returns:
The indexes of a design array corresponding to the variables names.
- Return type:
NDArray[int]
- has_current_value()[source]¶
Check if each variable has a current value.
- Returns:
Whether the current design value is defined for all variables.
- Return type:
- has_integer_variables()[source]¶
Check if the design space has at least one integer variable.
- Returns:
Whether the design space has at least one integer variable.
- Return type:
- initialize_missing_current_values()[source]¶
Initialize the current values of the design variables when missing.
Use:
the center of the design space when the lower and upper bounds are finite,
the lower bounds when the upper bounds are infinite,
the upper bounds when the lower bounds are infinite,
zero when the lower and upper bounds are infinite.
- Return type:
None
- items() a set-like object providing a view on D's items¶
- keys() a set-like object providing a view on D's keys¶
- normalize_grad(g_vect)[source]¶
Normalize an unnormalized gradient.
This method is based on the chain rule:
\[\frac{df(x)}{dx} = \frac{df(x)}{dx_u}\frac{dx_u}{dx} = \frac{df(x)}{dx_u}\frac{1}{u_b-l_b}\]where \(x_u = \frac{x-l_b}{u_b-l_b}\) is the normalized input vector, \(x\) is the unnormalized input vector and \(l_b\) and \(u_b\) are the lower and upper bounds of \(x\).
Then, the normalized gradient reads:
\[\frac{df(x)}{dx_u} = (u_b-l_b)\frac{df(x)}{dx}\]where \(\frac{df(x)}{dx}\) is the unnormalized one.
- normalize_vect(x_vect, minus_lb=True, out=None)[source]¶
Normalize a vector of the design space.
If minus_lb is True:
\[x_u = \frac{x-l_b}{u_b-l_b}\]where \(l_b\) and \(u_b\) are the lower and upper bounds of \(x\).
Otherwise:
\[x_u = \frac{x}{u_b-l_b}\]Unbounded variables are not normalized.
- Parameters:
x_vect (ArrayType) – The values of the design variables.
minus_lb (bool) –
If
True, remove the lower bounds at normalization.By default it is set to True.
out (ndarray | None) – The array to store the normalized vector. If
None, create a new array.
- Returns:
The normalized vector.
- Return type:
ArrayType
- pop(k[, d]) v, remove specified key and return the corresponding value.¶
If key is not found, d is returned if given, otherwise KeyError is raised.
- popitem() (k, v), remove and return some (key, value) pair¶
as a 2-tuple; but raise KeyError if D is empty.
- project_into_bounds(x_c, normalized=False)[source]¶
Project a vector onto the bounds, using a simple coordinate wise approach.
- remove_variable(name)[source]¶
Remove a variable from the design space.
- Parameters:
name (str) – The name of the variable to be removed.
- Return type:
None
- set_current_value(value)[source]¶
Set the current design value.
- Parameters:
value (ndarray | Mapping[str, ndarray] | OptimizationResult) – The value of the current design.
- Raises:
ValueError – If the value has a wrong dimension.
TypeError – If the value is neither a mapping of NumPy arrays, a NumPy array nor an
OptimizationResult.
- Return type:
None
- set_lower_bound(name, lower_bound)[source]¶
Set the lower bound of a variable.
- Parameters:
name (str) – The name of the variable.
lower_bound (ndarray | None) – The value of the lower bound.
- Raises:
ValueError – If the variable does not exist.
- Return type:
None
- set_upper_bound(name, upper_bound)[source]¶
Set the upper bound of a variable.
- Parameters:
name (str) – The name of the variable.
upper_bound (ndarray | None) – The value of the upper bound.
- Raises:
ValueError – If the variable does not exist.
- Return type:
None
- setdefault(k[, d]) D.get(k,d), also set D[k]=d if k not in D¶
- to_csv(output_file, fields=None, header_char='', **table_options)[source]¶
Export the design space to a CSV file.
- Parameters:
output_file (str | Path) – The path to the file.
fields (Sequence[str] | None) – The fields to be exported. If
None, export all fields.header_char (str) –
The header character.
By default it is set to “”.
**table_options (Any) – The names and values of additional attributes for the
PrettyTableview generated byDesignSpace.get_pretty_table().
- Return type:
None
- to_file(file_path, **options)[source]¶
Save the design space.
- Parameters:
file_path (str | Path) – The file path to save the design space. If the extension starts with “hdf”, the design space will be saved in an HDF file.
**options – The keyword reading options.
- Return type:
None
- to_hdf(file_path, append=False, hdf_node_path='')[source]¶
Export the design space to an HDF file.
- Parameters:
file_path (str | Path) – The path to the file to export the design space.
append (bool) –
If
True, appends the data in the file.By default it is set to False.
hdf_node_path (str) –
The path of the HDF node in which the design space should be exported. If empty, the root node is considered.
By default it is set to “”.
- Return type:
None
- transform_vect(vector, out=None)[source]¶
Map a point of the design space to a vector with components in \([0,1]\).
- Parameters:
vector (ndarray) – A point of the design space.
out (ndarray | None) – The array to store the transformed vector. If
None, create a new array.
- Returns:
A vector with components in \([0,1]\).
- Return type:
ndarray
- unnormalize_grad(g_vect)[source]¶
Unnormalize a normalized gradient.
This method is based on the chain rule:
\[\frac{df(x)}{dx} = \frac{df(x)}{dx_u}\frac{dx_u}{dx} = \frac{df(x)}{dx_u}\frac{1}{u_b-l_b}\]where \(x_u = \frac{x-l_b}{u_b-l_b}\) is the normalized input vector, \(x\) is the unnormalized input vector, \(\frac{df(x)}{dx_u}\) is the unnormalized gradient \(\frac{df(x)}{dx}\) is the normalized one, and \(l_b\) and \(u_b\) are the lower and upper bounds of \(x\).
- unnormalize_vect(x_vect, minus_lb=True, no_check=False, out=None)[source]¶
Unnormalize a normalized vector of the design space.
If minus_lb is True:
\[x = x_u(u_b-l_b) + l_b\]where \(x_u\) is the normalized input vector, \(x\) is the unnormalized input vector and \(l_b\) and \(u_b\) are the lower and upper bounds of \(x\).
Otherwise:
\[x = x_u(u_b-l_b)\]- Parameters:
x_vect (ArrayType) – The values of the design variables.
minus_lb (bool) –
Whether to remove the lower bounds at normalization.
By default it is set to True.
no_check (bool) –
Whether to check if the components are in \([0,1]\).
By default it is set to False.
out (ndarray | None) – The array to store the unnormalized vector. If
None, create a new array.
- Returns:
The unnormalized vector.
- Return type:
ArrayType
- untransform_vect(vector, no_check=False, out=None)[source]¶
Map a vector with components in \([0,1]\) to the design space.
- Parameters:
vector (ndarray) – A vector with components in \([0,1]\).
no_check (bool) –
Whether to check if the components are in \([0,1]\).
By default it is set to False.
out (ndarray | None) – The array to store the untransformed vector. If
None, create a new array.
- Returns:
A point of the variables space.
- Return type:
ndarray
- update([E, ]**F) None. Update D from mapping/iterable E and F.¶
If E present and has a .keys() method, does: for k in E: D[k] = E[k] If E present and lacks .keys() method, does: for (k, v) in E: D[k] = v In either case, this is followed by: for k, v in F.items(): D[k] = v
- values() an object providing a view on D's values¶
- DESIGN_SPACE_GROUP = 'design_space'¶
- LB_GROUP = 'l_b'¶
- NAMES_GROUP = 'names'¶
- NAME_GROUP = 'name'¶
- SEP = '!'¶
- SIZE_GROUP = 'size'¶
- UB_GROUP = 'u_b'¶
- VALUE_GROUP = 'value'¶
- VAR_TYPE_GROUP = 'var_type'¶
- dimension: int¶
The total dimension of the space, corresponding to the sum of the sizes of the variables.
- normalize: dict[str, ndarray]¶
The normalization policies of the variables components indexed by the variables names; if True, the component can be normalized.
- variable_types: dict[str, ndarray]¶
The types of the variables components, which can be any
DesignSpace.DesignVariableType.
Examples using DesignSpace¶
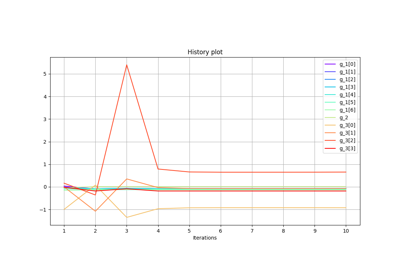
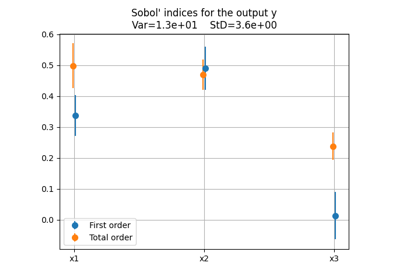
Example for exterior penalty applied to the Sobieski test case.
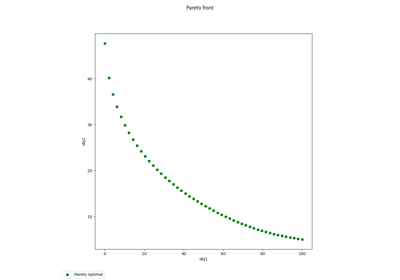
Pareto front on the Binh and Korn problem using a BiLevel formulation
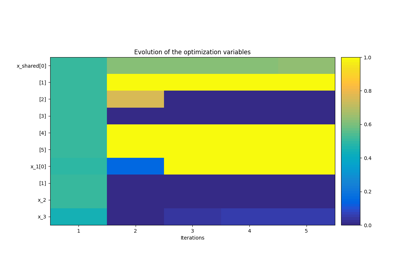
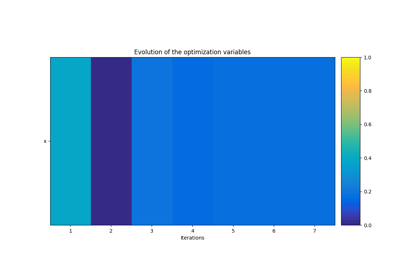
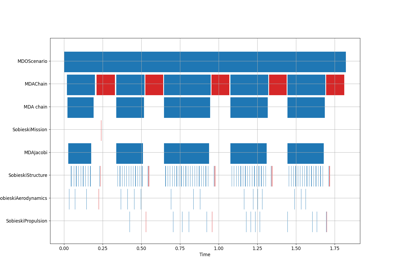
Application: Sobieski’s Super-Sonic Business Jet (MDO)
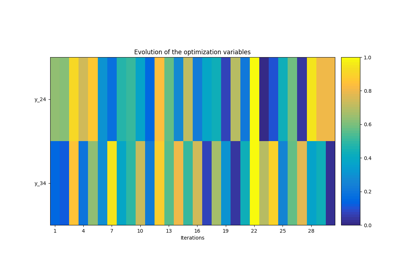
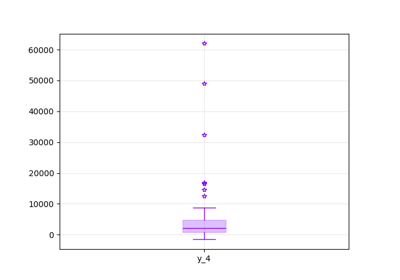
Simple disciplinary DOE example on the Sobieski SSBJ test case
Solve a 2D short cantilever topology optimization problem