Note
Go to the end to download the full example code
Parameter space¶
In this example, we will see the basics of ParameterSpace.
from __future__ import annotations
from gemseo import configure_logger
from gemseo import create_discipline
from gemseo import create_scenario
from gemseo.algos.parameter_space import ParameterSpace
from gemseo.post.dataset.scatter_plot_matrix import ScatterMatrix
configure_logger()
<RootLogger root (INFO)>
Firstly, a ParameterSpace does not require any mandatory argument.
Create a parameter space¶
parameter_space = ParameterSpace()
Then, we can add either deterministic variables
from their lower and upper bounds
(use ParameterSpace.add_variable()):
parameter_space.add_variable("x", l_b=-2.0, u_b=2.0)
or uncertain variables from their distribution names and parameters
(use ParameterSpace.add_random_variable()):
parameter_space.add_random_variable("y", "SPNormalDistribution", mu=0.0, sigma=1.0)
parameter_space
Warning
We cannot mix probability distributions from different families,
e.g. an OTDistribution and a SPDistribution.
We can check that the variables x and y are implemented as deterministic and uncertain variables respectively:
parameter_space.is_deterministic("x"), parameter_space.is_uncertain("y")
(True, True)
Note that when GEMSEO does not offer a class for the SciPy distribution,
we can use the generic GEMSEO class SPDistribution
to create any SciPy distribution
by setting interfaced_distribution to its SciPy name
and parameters as a dictionary of SciPy parameter names and values
(see the documentation of SciPy).
# parameter_space.add_random_variable(
# "y",
# "SPDistribution",
# interfaced_distribution="norm",
# parameters={"loc": 1.0, "scale": 2.0},
# )
A similar procedure can be followed
for OpenTURNS distributions for which
GEMSEO does not offer a class directly.
We can use the generic GEMSEO class OTDistribution
to create any OpenTURNS distribution
by setting interfaced_distribution to its OpenTURNS name
and parameters as a tuple of OpenTURNS parameter values
(see the documentation of OpenTURNS).
# parameter_space.add_random_variable(
# "y",
# "OTDistribution",
# interfaced_distribution="Normal",
# parameters=(1.0, 2.0),
# )
Sample from the parameter space¶
We can sample the uncertain variables from the ParameterSpace and
get values either as an array (default value):
sample = parameter_space.compute_samples(n_samples=2, as_dict=True)
sample
[{'y': array([-2.52574829])}, {'y': array([-0.48086384])}]
or as a dictionary:
sample = parameter_space.compute_samples(n_samples=4)
sample
array([[ 1.57128379],
[-0.5339523 ],
[ 0.06354121],
[-1.43210481]])
Sample a discipline over the parameter space¶
We can also sample a discipline over the parameter space. For simplicity,
we instantiate an AnalyticDiscipline from a dictionary of
expressions.
discipline = create_discipline("AnalyticDiscipline", expressions={"z": "x+y"})
From these parameter space and discipline, we build a DOEScenario
and execute it with a Latin Hypercube Sampling algorithm and 100 samples.
Warning
A Scenario deals with all variables available in the
DesignSpace. By inheritance, a DOEScenario deals
with all variables available in the ParameterSpace.
Thus, if we do not filter the uncertain variables, the
DOEScenario will consider all variables. In particular, the
deterministic variables will be considered as uniformly distributed.
scenario = create_scenario(
[discipline], "DisciplinaryOpt", "z", parameter_space, scenario_type="DOE"
)
scenario.execute({"algo": "lhs", "n_samples": 100})
INFO - 08:59:18:
INFO - 08:59:18: *** Start DOEScenario execution ***
INFO - 08:59:18: DOEScenario
INFO - 08:59:18: Disciplines: AnalyticDiscipline
INFO - 08:59:18: MDO formulation: DisciplinaryOpt
INFO - 08:59:18: Optimization problem:
INFO - 08:59:18: minimize z(x, y)
INFO - 08:59:18: with respect to x, y
INFO - 08:59:18: over the design space:
INFO - 08:59:18: +------+-------------+-------+-------------+-------+-------------------------+
INFO - 08:59:18: | Name | Lower bound | Value | Upper bound | Type | Distribution |
INFO - 08:59:18: +------+-------------+-------+-------------+-------+-------------------------+
INFO - 08:59:18: | x | -2 | None | 2 | float | |
INFO - 08:59:18: | y | -inf | 0 | inf | float | norm(mu=0.0, sigma=1.0) |
INFO - 08:59:18: +------+-------------+-------+-------------+-------+-------------------------+
INFO - 08:59:18: Solving optimization problem with algorithm lhs:
INFO - 08:59:18: 1%| | 1/100 [00:00<00:00, 439.38 it/sec, obj=3.12]
INFO - 08:59:18: 2%|▏ | 2/100 [00:00<00:00, 698.18 it/sec, obj=1.72]
INFO - 08:59:18: 3%|▎ | 3/100 [00:00<00:00, 882.08 it/sec, obj=0.181]
INFO - 08:59:18: 4%|▍ | 4/100 [00:00<00:00, 1018.59 it/sec, obj=3.76]
INFO - 08:59:18: 5%|▌ | 5/100 [00:00<00:00, 1122.67 it/sec, obj=2.15]
INFO - 08:59:18: 6%|▌ | 6/100 [00:00<00:00, 1204.28 it/sec, obj=-0.666]
INFO - 08:59:18: 7%|▋ | 7/100 [00:00<00:00, 1264.98 it/sec, obj=1.53]
INFO - 08:59:18: 8%|▊ | 8/100 [00:00<00:00, 1315.96 it/sec, obj=1.7]
INFO - 08:59:18: 9%|▉ | 9/100 [00:00<00:00, 1361.59 it/sec, obj=-2.27]
INFO - 08:59:18: 10%|█ | 10/100 [00:00<00:00, 1401.51 it/sec, obj=-2.08]
INFO - 08:59:18: 11%|█ | 11/100 [00:00<00:00, 1436.67 it/sec, obj=-2.8]
INFO - 08:59:18: 12%|█▏ | 12/100 [00:00<00:00, 1467.01 it/sec, obj=-1.31]
INFO - 08:59:18: 13%|█▎ | 13/100 [00:00<00:00, 1493.98 it/sec, obj=1.1]
INFO - 08:59:18: 14%|█▍ | 14/100 [00:00<00:00, 1513.99 it/sec, obj=0.38]
INFO - 08:59:18: 15%|█▌ | 15/100 [00:00<00:00, 1531.55 it/sec, obj=1.68]
INFO - 08:59:18: 16%|█▌ | 16/100 [00:00<00:00, 1550.72 it/sec, obj=0.672]
INFO - 08:59:18: 17%|█▋ | 17/100 [00:00<00:00, 1567.93 it/sec, obj=0.643]
INFO - 08:59:18: 18%|█▊ | 18/100 [00:00<00:00, 1583.65 it/sec, obj=0.568]
INFO - 08:59:18: 19%|█▉ | 19/100 [00:00<00:00, 1598.15 it/sec, obj=-0.277]
INFO - 08:59:18: 20%|██ | 20/100 [00:00<00:00, 1611.71 it/sec, obj=1.51]
INFO - 08:59:18: 21%|██ | 21/100 [00:00<00:00, 1623.90 it/sec, obj=1.83]
INFO - 08:59:18: 22%|██▏ | 22/100 [00:00<00:00, 1631.82 it/sec, obj=2.12]
INFO - 08:59:18: 23%|██▎ | 23/100 [00:00<00:00, 1639.82 it/sec, obj=0.526]
INFO - 08:59:18: 24%|██▍ | 24/100 [00:00<00:00, 1649.51 it/sec, obj=1.47]
INFO - 08:59:18: 25%|██▌ | 25/100 [00:00<00:00, 1658.33 it/sec, obj=-1.49]
INFO - 08:59:18: 26%|██▌ | 26/100 [00:00<00:00, 1666.75 it/sec, obj=-1.58]
INFO - 08:59:18: 27%|██▋ | 27/100 [00:00<00:00, 1674.32 it/sec, obj=1.59]
INFO - 08:59:18: 28%|██▊ | 28/100 [00:00<00:00, 1681.44 it/sec, obj=0.329]
INFO - 08:59:18: 29%|██▉ | 29/100 [00:00<00:00, 1688.15 it/sec, obj=-1.46]
INFO - 08:59:18: 30%|███ | 30/100 [00:00<00:00, 1689.14 it/sec, obj=-0.045]
INFO - 08:59:18: 31%|███ | 31/100 [00:00<00:00, 1694.93 it/sec, obj=-0.736]
INFO - 08:59:18: 32%|███▏ | 32/100 [00:00<00:00, 1700.57 it/sec, obj=0.867]
INFO - 08:59:18: 33%|███▎ | 33/100 [00:00<00:00, 1706.05 it/sec, obj=-3.12]
INFO - 08:59:18: 34%|███▍ | 34/100 [00:00<00:00, 1707.66 it/sec, obj=-0.252]
INFO - 08:59:18: 35%|███▌ | 35/100 [00:00<00:00, 1712.42 it/sec, obj=1.46]
INFO - 08:59:18: 36%|███▌ | 36/100 [00:00<00:00, 1717.20 it/sec, obj=-2.02]
INFO - 08:59:18: 37%|███▋ | 37/100 [00:00<00:00, 1709.58 it/sec, obj=-1.68]
INFO - 08:59:18: 38%|███▊ | 38/100 [00:00<00:00, 1711.15 it/sec, obj=-0.913]
INFO - 08:59:18: 39%|███▉ | 39/100 [00:00<00:00, 1715.32 it/sec, obj=-2.38]
INFO - 08:59:18: 40%|████ | 40/100 [00:00<00:00, 1719.44 it/sec, obj=1.07]
INFO - 08:59:18: 41%|████ | 41/100 [00:00<00:00, 1723.34 it/sec, obj=3.77]
INFO - 08:59:18: 42%|████▏ | 42/100 [00:00<00:00, 1727.18 it/sec, obj=-1.88]
INFO - 08:59:18: 43%|████▎ | 43/100 [00:00<00:00, 1730.84 it/sec, obj=0.116]
INFO - 08:59:18: 44%|████▍ | 44/100 [00:00<00:00, 1732.53 it/sec, obj=-1.51]
INFO - 08:59:18: 45%|████▌ | 45/100 [00:00<00:00, 1734.60 it/sec, obj=-0.0194]
INFO - 08:59:18: 46%|████▌ | 46/100 [00:00<00:00, 1737.66 it/sec, obj=0.984]
INFO - 08:59:18: 47%|████▋ | 47/100 [00:00<00:00, 1740.88 it/sec, obj=-0.34]
INFO - 08:59:18: 48%|████▊ | 48/100 [00:00<00:00, 1744.07 it/sec, obj=-0.941]
INFO - 08:59:18: 49%|████▉ | 49/100 [00:00<00:00, 1747.17 it/sec, obj=0.363]
INFO - 08:59:18: 50%|█████ | 50/100 [00:00<00:00, 1750.09 it/sec, obj=-1.01]
INFO - 08:59:18: 51%|█████ | 51/100 [00:00<00:00, 1753.07 it/sec, obj=-0.359]
INFO - 08:59:18: 52%|█████▏ | 52/100 [00:00<00:00, 1753.32 it/sec, obj=-3.06]
INFO - 08:59:18: 53%|█████▎ | 53/100 [00:00<00:00, 1755.65 it/sec, obj=2.34]
INFO - 08:59:18: 54%|█████▍ | 54/100 [00:00<00:00, 1758.41 it/sec, obj=-0.262]
INFO - 08:59:18: 55%|█████▌ | 55/100 [00:00<00:00, 1761.10 it/sec, obj=0.812]
INFO - 08:59:18: 56%|█████▌ | 56/100 [00:00<00:00, 1763.62 it/sec, obj=-2.47]
INFO - 08:59:18: 57%|█████▋ | 57/100 [00:00<00:00, 1766.28 it/sec, obj=1.49]
INFO - 08:59:18: 58%|█████▊ | 58/100 [00:00<00:00, 1768.67 it/sec, obj=0.268]
INFO - 08:59:18: 59%|█████▉ | 59/100 [00:00<00:00, 1769.67 it/sec, obj=0.559]
INFO - 08:59:18: 60%|██████ | 60/100 [00:00<00:00, 1770.86 it/sec, obj=-2.01]
INFO - 08:59:18: 61%|██████ | 61/100 [00:00<00:00, 1772.88 it/sec, obj=-0.854]
INFO - 08:59:18: 62%|██████▏ | 62/100 [00:00<00:00, 1774.97 it/sec, obj=1.61]
INFO - 08:59:18: 63%|██████▎ | 63/100 [00:00<00:00, 1776.97 it/sec, obj=-2.64]
INFO - 08:59:18: 64%|██████▍ | 64/100 [00:00<00:00, 1778.97 it/sec, obj=0.818]
INFO - 08:59:18: 65%|██████▌ | 65/100 [00:00<00:00, 1780.90 it/sec, obj=1.04]
INFO - 08:59:18: 66%|██████▌ | 66/100 [00:00<00:00, 1782.83 it/sec, obj=-0.832]
INFO - 08:59:18: 67%|██████▋ | 67/100 [00:00<00:00, 1783.02 it/sec, obj=0.692]
INFO - 08:59:18: 68%|██████▊ | 68/100 [00:00<00:00, 1783.73 it/sec, obj=-3.33]
INFO - 08:59:18: 69%|██████▉ | 69/100 [00:00<00:00, 1784.66 it/sec, obj=0.47]
INFO - 08:59:18: 70%|███████ | 70/100 [00:00<00:00, 1775.00 it/sec, obj=0.445]
INFO - 08:59:18: 71%|███████ | 71/100 [00:00<00:00, 1775.62 it/sec, obj=0.402]
INFO - 08:59:18: 72%|███████▏ | 72/100 [00:00<00:00, 1776.84 it/sec, obj=2.77]
INFO - 08:59:18: 73%|███████▎ | 73/100 [00:00<00:00, 1778.22 it/sec, obj=-0.256]
INFO - 08:59:18: 74%|███████▍ | 74/100 [00:00<00:00, 1777.87 it/sec, obj=3.36]
INFO - 08:59:18: 75%|███████▌ | 75/100 [00:00<00:00, 1779.14 it/sec, obj=-0.229]
INFO - 08:59:18: 76%|███████▌ | 76/100 [00:00<00:00, 1780.74 it/sec, obj=-0.739]
INFO - 08:59:18: 77%|███████▋ | 77/100 [00:00<00:00, 1782.34 it/sec, obj=0.808]
INFO - 08:59:18: 78%|███████▊ | 78/100 [00:00<00:00, 1783.87 it/sec, obj=-0.377]
INFO - 08:59:18: 79%|███████▉ | 79/100 [00:00<00:00, 1785.44 it/sec, obj=0.708]
INFO - 08:59:18: 80%|████████ | 80/100 [00:00<00:00, 1786.97 it/sec, obj=-0.874]
INFO - 08:59:18: 81%|████████ | 81/100 [00:00<00:00, 1787.54 it/sec, obj=-1.29]
INFO - 08:59:18: 82%|████████▏ | 82/100 [00:00<00:00, 1788.19 it/sec, obj=0.505]
INFO - 08:59:18: 83%|████████▎ | 83/100 [00:00<00:00, 1789.59 it/sec, obj=1.99]
INFO - 08:59:18: 84%|████████▍ | 84/100 [00:00<00:00, 1783.42 it/sec, obj=0.574]
INFO - 08:59:18: 85%|████████▌ | 85/100 [00:00<00:00, 1783.32 it/sec, obj=-2.06]
INFO - 08:59:18: 86%|████████▌ | 86/100 [00:00<00:00, 1784.38 it/sec, obj=-1.49]
INFO - 08:59:18: 87%|████████▋ | 87/100 [00:00<00:00, 1785.46 it/sec, obj=0.61]
INFO - 08:59:18: 88%|████████▊ | 88/100 [00:00<00:00, 1785.71 it/sec, obj=0.542]
INFO - 08:59:18: 89%|████████▉ | 89/100 [00:00<00:00, 1785.93 it/sec, obj=-1.5]
INFO - 08:59:18: 90%|█████████ | 90/100 [00:00<00:00, 1786.87 it/sec, obj=0.201]
INFO - 08:59:18: 91%|█████████ | 91/100 [00:00<00:00, 1788.05 it/sec, obj=0.949]
INFO - 08:59:18: 92%|█████████▏| 92/100 [00:00<00:00, 1789.37 it/sec, obj=-1.86]
INFO - 08:59:18: 93%|█████████▎| 93/100 [00:00<00:00, 1790.64 it/sec, obj=-0.0722]
INFO - 08:59:18: 94%|█████████▍| 94/100 [00:00<00:00, 1791.83 it/sec, obj=-0.407]
INFO - 08:59:18: 95%|█████████▌| 95/100 [00:00<00:00, 1793.07 it/sec, obj=0.194]
INFO - 08:59:18: 96%|█████████▌| 96/100 [00:00<00:00, 1793.00 it/sec, obj=-0.207]
INFO - 08:59:18: 97%|█████████▋| 97/100 [00:00<00:00, 1793.10 it/sec, obj=0.462]
INFO - 08:59:18: 98%|█████████▊| 98/100 [00:00<00:00, 1794.09 it/sec, obj=-2.37]
INFO - 08:59:18: 99%|█████████▉| 99/100 [00:00<00:00, 1795.07 it/sec, obj=1.32]
INFO - 08:59:18: 100%|██████████| 100/100 [00:00<00:00, 1796.11 it/sec, obj=-2.21]
INFO - 08:59:18: Optimization result:
INFO - 08:59:18: Optimizer info:
INFO - 08:59:18: Status: None
INFO - 08:59:18: Message: None
INFO - 08:59:18: Number of calls to the objective function by the optimizer: 100
INFO - 08:59:18: Solution:
INFO - 08:59:18: Objective: -3.3284373246961634
INFO - 08:59:18: Design space:
INFO - 08:59:18: +------+-------------+--------------------+-------------+-------+-------------------------+
INFO - 08:59:18: | Name | Lower bound | Value | Upper bound | Type | Distribution |
INFO - 08:59:18: +------+-------------+--------------------+-------------+-------+-------------------------+
INFO - 08:59:18: | x | -2 | -1.959995425007306 | 2 | float | |
INFO - 08:59:18: | y | -inf | -1.368441899688857 | inf | float | norm(mu=0.0, sigma=1.0) |
INFO - 08:59:18: +------+-------------+--------------------+-------------+-------+-------------------------+
INFO - 08:59:18: *** End DOEScenario execution (time: 0:00:00.079271) ***
{'eval_jac': False, 'n_samples': 100, 'algo': 'lhs'}
We can visualize the result by encapsulating the database in
a Dataset:
dataset = scenario.to_dataset(opt_naming=False)
This visualization can be tabular for example:
dataset
or graphical by means of a scatter plot matrix for example:
ScatterMatrix(dataset).execute(save=False, show=True)
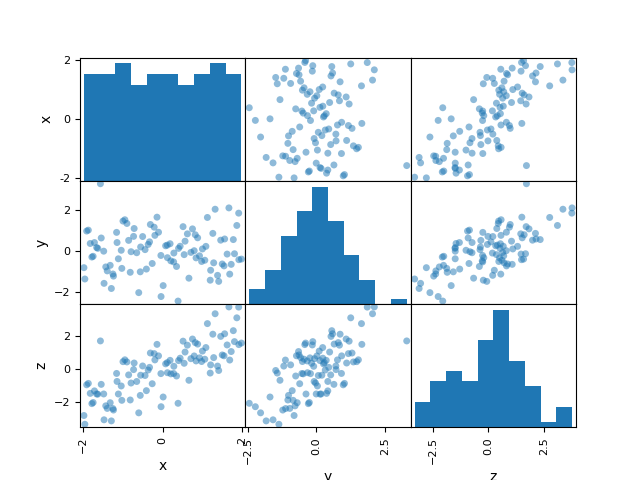
[<Figure size 640x480 with 9 Axes>]
Sample a discipline over the uncertain space¶
If we want to sample a discipline over the uncertain space, we need to filter the uncertain variables:
parameter_space.filter(parameter_space.uncertain_variables)
Then, we create a new scenario from this parameter space containing only the uncertain variables and execute it.
scenario = create_scenario(
[discipline], "DisciplinaryOpt", "z", parameter_space, scenario_type="DOE"
)
scenario.execute({"algo": "lhs", "n_samples": 100})
INFO - 08:59:19:
INFO - 08:59:19: *** Start DOEScenario execution ***
INFO - 08:59:19: DOEScenario
INFO - 08:59:19: Disciplines: AnalyticDiscipline
INFO - 08:59:19: MDO formulation: DisciplinaryOpt
INFO - 08:59:19: Optimization problem:
INFO - 08:59:19: minimize z(y)
INFO - 08:59:19: with respect to y
INFO - 08:59:19: over the design space:
INFO - 08:59:19: +------+-------------------------+
INFO - 08:59:19: | Name | Distribution |
INFO - 08:59:19: +------+-------------------------+
INFO - 08:59:19: | y | norm(mu=0.0, sigma=1.0) |
INFO - 08:59:19: +------+-------------------------+
INFO - 08:59:19: Solving optimization problem with algorithm lhs:
INFO - 08:59:19: 1%| | 1/100 [00:00<00:00, 1791.67 it/sec, obj=-0.641]
INFO - 08:59:19: 2%|▏ | 2/100 [00:00<00:00, 1774.99 it/sec, obj=-0.394]
INFO - 08:59:19: 3%|▎ | 3/100 [00:00<00:00, 1807.89 it/sec, obj=0.551]
INFO - 08:59:19: 4%|▍ | 4/100 [00:00<00:00, 1825.00 it/sec, obj=0.944]
INFO - 08:59:19: 5%|▌ | 5/100 [00:00<00:00, 1836.87 it/sec, obj=-2.12]
INFO - 08:59:19: 6%|▌ | 6/100 [00:00<00:00, 1827.32 it/sec, obj=-1.64]
INFO - 08:59:19: 7%|▋ | 7/100 [00:00<00:00, 1824.74 it/sec, obj=0.656]
INFO - 08:59:19: 8%|▊ | 8/100 [00:00<00:00, 1832.17 it/sec, obj=-0.612]
INFO - 08:59:19: 9%|▉ | 9/100 [00:00<00:00, 1839.88 it/sec, obj=0.736]
INFO - 08:59:19: 10%|█ | 10/100 [00:00<00:00, 1845.27 it/sec, obj=0.36]
INFO - 08:59:19: 11%|█ | 11/100 [00:00<00:00, 1849.27 it/sec, obj=-0.31]
INFO - 08:59:19: 12%|█▏ | 12/100 [00:00<00:00, 1853.15 it/sec, obj=0.324]
INFO - 08:59:19: 13%|█▎ | 13/100 [00:00<00:00, 1633.05 it/sec, obj=-1.73]
INFO - 08:59:19: 14%|█▍ | 14/100 [00:00<00:00, 1646.85 it/sec, obj=0.494]
INFO - 08:59:19: 15%|█▌ | 15/100 [00:00<00:00, 1659.97 it/sec, obj=-0.148]
INFO - 08:59:19: 16%|█▌ | 16/100 [00:00<00:00, 1672.54 it/sec, obj=1.1]
INFO - 08:59:19: 17%|█▋ | 17/100 [00:00<00:00, 1683.90 it/sec, obj=-0.716]
INFO - 08:59:19: 18%|█▊ | 18/100 [00:00<00:00, 1693.98 it/sec, obj=0.0421]
INFO - 08:59:19: 19%|█▉ | 19/100 [00:00<00:00, 1699.15 it/sec, obj=0.256]
INFO - 08:59:19: 20%|██ | 20/100 [00:00<00:00, 1704.59 it/sec, obj=-1.45]
INFO - 08:59:19: 21%|██ | 21/100 [00:00<00:00, 1711.63 it/sec, obj=0.637]
INFO - 08:59:19: 22%|██▏ | 22/100 [00:00<00:00, 1718.62 it/sec, obj=1.97]
INFO - 08:59:19: 23%|██▎ | 23/100 [00:00<00:00, 1724.79 it/sec, obj=-0.208]
INFO - 08:59:19: 24%|██▍ | 24/100 [00:00<00:00, 1730.26 it/sec, obj=0.18]
INFO - 08:59:19: 25%|██▌ | 25/100 [00:00<00:00, 1735.45 it/sec, obj=0.000485]
INFO - 08:59:19: 26%|██▌ | 26/100 [00:00<00:00, 1740.51 it/sec, obj=1.17]
INFO - 08:59:19: 27%|██▋ | 27/100 [00:00<00:00, 1742.06 it/sec, obj=-0.305]
INFO - 08:59:19: 28%|██▊ | 28/100 [00:00<00:00, 1744.46 it/sec, obj=0.68]
INFO - 08:59:19: 29%|██▉ | 29/100 [00:00<00:00, 1748.53 it/sec, obj=-0.932]
INFO - 08:59:19: 30%|███ | 30/100 [00:00<00:00, 1748.74 it/sec, obj=0.901]
INFO - 08:59:19: 31%|███ | 31/100 [00:00<00:00, 1751.68 it/sec, obj=0.454]
INFO - 08:59:19: 32%|███▏ | 32/100 [00:00<00:00, 1755.28 it/sec, obj=-1.16]
INFO - 08:59:19: 33%|███▎ | 33/100 [00:00<00:00, 1758.71 it/sec, obj=1.44]
INFO - 08:59:19: 34%|███▍ | 34/100 [00:00<00:00, 1759.79 it/sec, obj=0.798]
INFO - 08:59:19: 35%|███▌ | 35/100 [00:00<00:00, 1761.07 it/sec, obj=1.59]
INFO - 08:59:19: 36%|███▌ | 36/100 [00:00<00:00, 1763.96 it/sec, obj=2.05]
INFO - 08:59:19: 37%|███▋ | 37/100 [00:00<00:00, 1767.17 it/sec, obj=-0.26]
INFO - 08:59:19: 38%|███▊ | 38/100 [00:00<00:00, 1769.95 it/sec, obj=0.874]
INFO - 08:59:19: 39%|███▉ | 39/100 [00:00<00:00, 1772.64 it/sec, obj=0.832]
INFO - 08:59:19: 40%|████ | 40/100 [00:00<00:00, 1775.35 it/sec, obj=-1.38]
INFO - 08:59:19: 41%|████ | 41/100 [00:00<00:00, 1777.80 it/sec, obj=1.52]
INFO - 08:59:19: 42%|████▏ | 42/100 [00:00<00:00, 1776.85 it/sec, obj=-0.522]
INFO - 08:59:19: 43%|████▎ | 43/100 [00:00<00:00, 1778.67 it/sec, obj=1.4]
INFO - 08:59:19: 44%|████▍ | 44/100 [00:00<00:00, 1780.80 it/sec, obj=-0.484]
INFO - 08:59:19: 45%|████▌ | 45/100 [00:00<00:00, 1782.74 it/sec, obj=-0.91]
INFO - 08:59:19: 46%|████▌ | 46/100 [00:00<00:00, 1784.88 it/sec, obj=0.343]
INFO - 08:59:19: 47%|████▋ | 47/100 [00:00<00:00, 1786.90 it/sec, obj=-0.441]
INFO - 08:59:19: 48%|████▊ | 48/100 [00:00<00:00, 1788.70 it/sec, obj=-0.871]
INFO - 08:59:19: 49%|████▉ | 49/100 [00:00<00:00, 1788.57 it/sec, obj=2.67]
INFO - 08:59:19: 50%|█████ | 50/100 [00:00<00:00, 1788.54 it/sec, obj=0.217]
INFO - 08:59:19: 51%|█████ | 51/100 [00:00<00:00, 1789.95 it/sec, obj=-0.425]
INFO - 08:59:19: 52%|█████▏ | 52/100 [00:00<00:00, 1791.66 it/sec, obj=0.113]
INFO - 08:59:19: 53%|█████▎ | 53/100 [00:00<00:00, 1793.20 it/sec, obj=-0.377]
INFO - 08:59:19: 54%|█████▍ | 54/100 [00:00<00:00, 1794.81 it/sec, obj=-1.19]
INFO - 08:59:19: 55%|█████▌ | 55/100 [00:00<00:00, 1796.43 it/sec, obj=-0.528]
INFO - 08:59:19: 56%|█████▌ | 56/100 [00:00<00:00, 1796.98 it/sec, obj=-2.64]
INFO - 08:59:19: 57%|█████▋ | 57/100 [00:00<00:00, 1797.29 it/sec, obj=-0.0776]
INFO - 08:59:19: 58%|█████▊ | 58/100 [00:00<00:00, 1798.67 it/sec, obj=1.08]
INFO - 08:59:19: 59%|█████▉ | 59/100 [00:00<00:00, 1799.96 it/sec, obj=-2.05]
INFO - 08:59:19: 60%|██████ | 60/100 [00:00<00:00, 1801.39 it/sec, obj=0.0555]
INFO - 08:59:19: 61%|██████ | 61/100 [00:00<00:00, 1802.60 it/sec, obj=-1.84]
INFO - 08:59:19: 62%|██████▏ | 62/100 [00:00<00:00, 1803.94 it/sec, obj=0.4]
INFO - 08:59:19: 63%|██████▎ | 63/100 [00:00<00:00, 1805.12 it/sec, obj=-0.195]
INFO - 08:59:19: 64%|██████▍ | 64/100 [00:00<00:00, 1804.54 it/sec, obj=-0.578]
INFO - 08:59:19: 65%|██████▌ | 65/100 [00:00<00:00, 1804.59 it/sec, obj=-0.977]
INFO - 08:59:19: 66%|██████▌ | 66/100 [00:00<00:00, 1805.73 it/sec, obj=-0.114]
INFO - 08:59:19: 67%|██████▋ | 67/100 [00:00<00:00, 1806.90 it/sec, obj=0.587]
INFO - 08:59:19: 68%|██████▊ | 68/100 [00:00<00:00, 1808.05 it/sec, obj=-0.0679]
INFO - 08:59:19: 69%|██████▉ | 69/100 [00:00<00:00, 1806.43 it/sec, obj=-0.0218]
INFO - 08:59:19: 70%|███████ | 70/100 [00:00<00:00, 1806.87 it/sec, obj=-0.228]
INFO - 08:59:19: 71%|███████ | 71/100 [00:00<00:00, 1806.41 it/sec, obj=1.21]
INFO - 08:59:19: 72%|███████▏ | 72/100 [00:00<00:00, 1806.56 it/sec, obj=-0.34]
INFO - 08:59:19: 73%|███████▎ | 73/100 [00:00<00:00, 1807.40 it/sec, obj=0.513]
INFO - 08:59:19: 74%|███████▍ | 74/100 [00:00<00:00, 1808.44 it/sec, obj=1.67]
INFO - 08:59:19: 75%|███████▌ | 75/100 [00:00<00:00, 1809.52 it/sec, obj=0.557]
INFO - 08:59:19: 76%|███████▌ | 76/100 [00:00<00:00, 1810.65 it/sec, obj=0.431]
INFO - 08:59:19: 77%|███████▋ | 77/100 [00:00<00:00, 1811.69 it/sec, obj=-1.31]
INFO - 08:59:19: 78%|███████▊ | 78/100 [00:00<00:00, 1812.81 it/sec, obj=-0.678]
INFO - 08:59:19: 79%|███████▉ | 79/100 [00:00<00:00, 1811.98 it/sec, obj=-1.01]
INFO - 08:59:19: 80%|████████ | 80/100 [00:00<00:00, 1812.73 it/sec, obj=0.246]
INFO - 08:59:19: 81%|████████ | 81/100 [00:00<00:00, 1813.73 it/sec, obj=1.29]
INFO - 08:59:19: 82%|████████▏ | 82/100 [00:00<00:00, 1814.56 it/sec, obj=0.75]
INFO - 08:59:19: 83%|████████▎ | 83/100 [00:00<00:00, 1805.33 it/sec, obj=-1.54]
INFO - 08:59:19: 84%|████████▍ | 84/100 [00:00<00:00, 1804.50 it/sec, obj=-0.156]
INFO - 08:59:19: 85%|████████▌ | 85/100 [00:00<00:00, 1805.28 it/sec, obj=1.87]
INFO - 08:59:19: 86%|████████▌ | 86/100 [00:00<00:00, 1804.33 it/sec, obj=-1.08]
INFO - 08:59:19: 87%|████████▋ | 87/100 [00:00<00:00, 1804.95 it/sec, obj=-0.647]
INFO - 08:59:19: 88%|████████▊ | 88/100 [00:00<00:00, 1805.86 it/sec, obj=0.968]
INFO - 08:59:19: 89%|████████▉ | 89/100 [00:00<00:00, 1806.79 it/sec, obj=-0.773]
INFO - 08:59:19: 90%|█████████ | 90/100 [00:00<00:00, 1807.58 it/sec, obj=1.26]
INFO - 08:59:19: 91%|█████████ | 91/100 [00:00<00:00, 1808.46 it/sec, obj=0.166]
INFO - 08:59:19: 92%|█████████▏| 92/100 [00:00<00:00, 1809.34 it/sec, obj=0.29]
INFO - 08:59:19: 93%|█████████▎| 93/100 [00:00<00:00, 1809.17 it/sec, obj=0.127]
INFO - 08:59:19: 94%|█████████▍| 94/100 [00:00<00:00, 1809.14 it/sec, obj=-1.26]
INFO - 08:59:19: 95%|█████████▌| 95/100 [00:00<00:00, 1809.87 it/sec, obj=1.01]
INFO - 08:59:19: 96%|█████████▌| 96/100 [00:00<00:00, 1810.56 it/sec, obj=0.0819]
INFO - 08:59:19: 97%|█████████▋| 97/100 [00:00<00:00, 1811.41 it/sec, obj=-1.09]
INFO - 08:59:19: 98%|█████████▊| 98/100 [00:00<00:00, 1812.26 it/sec, obj=-0.762]
INFO - 08:59:19: 99%|█████████▉| 99/100 [00:00<00:00, 1813.11 it/sec, obj=-0.0429]
INFO - 08:59:19: 100%|██████████| 100/100 [00:00<00:00, 1813.20 it/sec, obj=-0.813]
INFO - 08:59:19: Optimization result:
INFO - 08:59:19: Optimizer info:
INFO - 08:59:19: Status: None
INFO - 08:59:19: Message: None
INFO - 08:59:19: Number of calls to the objective function by the optimizer: 100
INFO - 08:59:19: Solution:
INFO - 08:59:19: Objective: -2.6379682068246657
INFO - 08:59:19: Design space:
INFO - 08:59:19: +------+-------------------------+
INFO - 08:59:19: | Name | Distribution |
INFO - 08:59:19: +------+-------------------------+
INFO - 08:59:19: | y | norm(mu=0.0, sigma=1.0) |
INFO - 08:59:19: +------+-------------------------+
INFO - 08:59:19: *** End DOEScenario execution (time: 0:00:00.077280) ***
{'eval_jac': False, 'n_samples': 100, 'algo': 'lhs'}
Finally, we build a dataset from the disciplinary cache and visualize it. We can see that the deterministic variable ‘x’ is set to its default value for all evaluations, contrary to the previous case where we were considering the whole parameter space.
dataset = scenario.to_dataset(opt_naming=False)
dataset
Total running time of the script: (0 minutes 0.542 seconds)
