Note
Go to the end to download the full example code
Robustness¶
In this example, we illustrate the use of the Robustness plot
on the Sobieski’s SSBJ problem.
from __future__ import annotations
from gemseo import configure_logger
from gemseo import create_discipline
from gemseo import create_scenario
from gemseo.problems.mdo.sobieski.core.design_space import SobieskiDesignSpace
Import¶
The first step is to import some high-level functions and a method to get the design space.
configure_logger()
<RootLogger root (INFO)>
Description¶
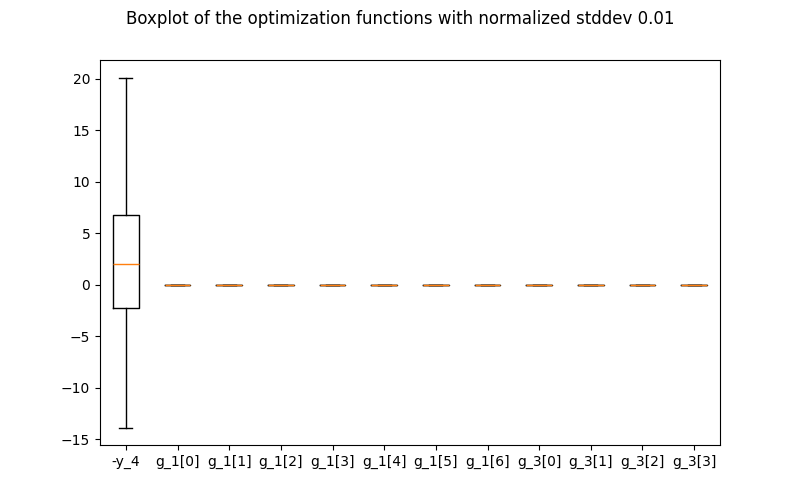
In the Robustness post-processing,
the robustness of the optimum is represented by a box plot. Using the
quadratic approximations of all the output functions, we
propagate analytically a normal distribution with 1% standard deviation
on all the design variables, assuming no cross-correlations of inputs,
to obtain the mean and standard deviation of the resulting normal
distribution. A series of samples are randomly generated from the resulting
distribution, whose quartiles are plotted, relatively to the values of
the function at the optimum. For each function (in abscissa), the plot
shows the extreme values encountered in the samples (top and bottom
bars). Then, 95% of the values are within the blue boxes. The average is
given by the red bar.
Create disciplines¶
At this point, we instantiate the disciplines of Sobieski’s SSBJ problem: Propulsion, Aerodynamics, Structure and Mission
disciplines = create_discipline([
"SobieskiPropulsion",
"SobieskiAerodynamics",
"SobieskiStructure",
"SobieskiMission",
])
Create design space¶
We also create the SobieskiDesignSpace.
design_space = SobieskiDesignSpace()
Create and execute scenario¶
The next step is to build an MDO scenario in order to maximize the range, encoded ‘y_4’, with respect to the design parameters, while satisfying the inequality constraints ‘g_1’, ‘g_2’ and ‘g_3’. We can use the MDF formulation, the SLSQP optimization algorithm and a maximum number of iterations equal to 100.
scenario = create_scenario(
disciplines,
"MDF",
"y_4",
design_space,
maximize_objective=True,
)
scenario.set_differentiation_method()
for constraint in ["g_1", "g_2", "g_3"]:
scenario.add_constraint(constraint, constraint_type="ineq")
scenario.execute({"algo": "SLSQP", "max_iter": 10})
INFO - 08:59:50:
INFO - 08:59:50: *** Start MDOScenario execution ***
INFO - 08:59:50: MDOScenario
INFO - 08:59:50: Disciplines: SobieskiAerodynamics SobieskiMission SobieskiPropulsion SobieskiStructure
INFO - 08:59:50: MDO formulation: MDF
INFO - 08:59:50: Optimization problem:
INFO - 08:59:50: minimize -y_4(x_shared, x_1, x_2, x_3)
INFO - 08:59:50: with respect to x_1, x_2, x_3, x_shared
INFO - 08:59:50: subject to constraints:
INFO - 08:59:50: g_1(x_shared, x_1, x_2, x_3) <= 0.0
INFO - 08:59:50: g_2(x_shared, x_1, x_2, x_3) <= 0.0
INFO - 08:59:50: g_3(x_shared, x_1, x_2, x_3) <= 0.0
INFO - 08:59:50: over the design space:
INFO - 08:59:50: +-------------+-------------+-------+-------------+-------+
INFO - 08:59:50: | Name | Lower bound | Value | Upper bound | Type |
INFO - 08:59:50: +-------------+-------------+-------+-------------+-------+
INFO - 08:59:50: | x_shared[0] | 0.01 | 0.05 | 0.09 | float |
INFO - 08:59:50: | x_shared[1] | 30000 | 45000 | 60000 | float |
INFO - 08:59:50: | x_shared[2] | 1.4 | 1.6 | 1.8 | float |
INFO - 08:59:50: | x_shared[3] | 2.5 | 5.5 | 8.5 | float |
INFO - 08:59:50: | x_shared[4] | 40 | 55 | 70 | float |
INFO - 08:59:50: | x_shared[5] | 500 | 1000 | 1500 | float |
INFO - 08:59:50: | x_1[0] | 0.1 | 0.25 | 0.4 | float |
INFO - 08:59:50: | x_1[1] | 0.75 | 1 | 1.25 | float |
INFO - 08:59:50: | x_2 | 0.75 | 1 | 1.25 | float |
INFO - 08:59:50: | x_3 | 0.1 | 0.5 | 1 | float |
INFO - 08:59:50: +-------------+-------------+-------+-------------+-------+
INFO - 08:59:50: Solving optimization problem with algorithm SLSQP:
INFO - 08:59:50: 10%|█ | 1/10 [00:00<00:00, 11.29 it/sec, obj=-536]
INFO - 08:59:50: 20%|██ | 2/10 [00:00<00:01, 7.97 it/sec, obj=-2.12e+3]
WARNING - 08:59:51: MDAJacobi has reached its maximum number of iterations but the normed residual 1.7130677857005655e-05 is still above the tolerance 1e-06.
INFO - 08:59:51: 30%|███ | 3/10 [00:00<00:01, 6.71 it/sec, obj=-3.75e+3]
INFO - 08:59:51: 40%|████ | 4/10 [00:00<00:00, 6.40 it/sec, obj=-3.96e+3]
INFO - 08:59:51: 50%|█████ | 5/10 [00:00<00:00, 6.23 it/sec, obj=-3.96e+3]
INFO - 08:59:51: Optimization result:
INFO - 08:59:51: Optimizer info:
INFO - 08:59:51: Status: 8
INFO - 08:59:51: Message: Positive directional derivative for linesearch
INFO - 08:59:51: Number of calls to the objective function by the optimizer: 6
INFO - 08:59:51: Solution:
INFO - 08:59:51: The solution is feasible.
INFO - 08:59:51: Objective: -3963.408265187933
INFO - 08:59:51: Standardized constraints:
INFO - 08:59:51: g_1 = [-0.01806104 -0.03334642 -0.04424946 -0.0518346 -0.05732607 -0.13720865
INFO - 08:59:51: -0.10279135]
INFO - 08:59:51: g_2 = 3.333278582928756e-06
INFO - 08:59:51: g_3 = [-7.67181773e-01 -2.32818227e-01 8.30379541e-07 -1.83255000e-01]
INFO - 08:59:51: Design space:
INFO - 08:59:51: +-------------+-------------+---------------------+-------------+-------+
INFO - 08:59:51: | Name | Lower bound | Value | Upper bound | Type |
INFO - 08:59:51: +-------------+-------------+---------------------+-------------+-------+
INFO - 08:59:51: | x_shared[0] | 0.01 | 0.06000083331964572 | 0.09 | float |
INFO - 08:59:51: | x_shared[1] | 30000 | 60000 | 60000 | float |
INFO - 08:59:51: | x_shared[2] | 1.4 | 1.4 | 1.8 | float |
INFO - 08:59:51: | x_shared[3] | 2.5 | 2.5 | 8.5 | float |
INFO - 08:59:51: | x_shared[4] | 40 | 70 | 70 | float |
INFO - 08:59:51: | x_shared[5] | 500 | 1500 | 1500 | float |
INFO - 08:59:51: | x_1[0] | 0.1 | 0.4 | 0.4 | float |
INFO - 08:59:51: | x_1[1] | 0.75 | 0.75 | 1.25 | float |
INFO - 08:59:51: | x_2 | 0.75 | 0.75 | 1.25 | float |
INFO - 08:59:51: | x_3 | 0.1 | 0.1562448753887276 | 1 | float |
INFO - 08:59:51: +-------------+-------------+---------------------+-------------+-------+
INFO - 08:59:51: *** End MDOScenario execution (time: 0:00:00.920788) ***
{'max_iter': 10, 'algo': 'SLSQP'}
Post-process scenario¶
Lastly, we post-process the scenario by means of the Robustness
which plots any of the constraint or
objective functions w.r.t. the optimization iterations or sampling snapshots.
Tip
Each post-processing method requires different inputs and offers a variety
of customization options. Use the high-level function
get_post_processing_options_schema() to print a table with
the options for any post-processing algorithm.
Or refer to our dedicated page:
Post-processing algorithms.
scenario.post_process("Robustness", save=False, show=True)
<gemseo.post.robustness.Robustness object at 0x7f1db0e37850>
Total running time of the script: (0 minutes 1.120 seconds)
