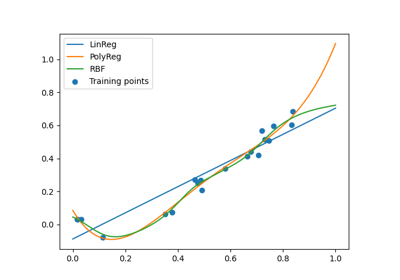
polyreg module¶
Polynomial regression model.
Polynomial regression is a particular case of the linear regression, where the input data is transformed before the regression is applied. This transform consists of creating a matrix of monomials by raising the input data to different powers up to a certain degree \(D\). In the case where there is only one input variable, the input data \((x_i)_{i=1, \dots, n}\in\mathbb{R}^n\) is transformed into the Vandermonde matrix:
The output variable is expressed as a weighted sum of monomials:
where the coefficients \(w_1, w_2, ..., w_d\) and the intercept \(w_0\) are estimated by least square regression.
In the case of a multidimensional input, i.e. \(X = (x_{ij})_{i=1,\dots,n; j=1,\dots,m}\), where \(n\) is the number of samples and \(m\) is the number of input variables, the Vandermonde matrix is expressed through different combinations of monomials of degree \(d, (1 \leq d \leq D)\); e.g. for three variables \((x, y, z)\) and degree \(D=3\), the different terms are \(x\), \(y\), \(z\), \(x^2\), \(xy\), \(xz\), \(y^2\), \(yz\), \(z^2\), \(x^3\), \(x^2y\) etc. More generally, for \(m\) input variables, the total number of monomials of degree \(1 \leq d \leq D\) is given by \(P = \binom{m+D}{m} = \frac{(m+D)!}{m!D!}\). In the case of 3 input variables given above, the total number of monomial combinations of degree lesser than or equal to three is thus \(P = \binom{6}{3} = 20\). The linear regression has to identify the coefficients \(w_1, \dots, w_P\), in addition to the intercept \(w_0\).
Dependence¶
The polynomial regression model relies on the LinearRegression and PolynomialFeatures classes of the scikit-learn library.
- class gemseo.mlearning.regression.polyreg.PolynomialRegressor(data, degree, transformer=mappingproxy({}), input_names=None, output_names=None, fit_intercept=True, penalty_level=0.0, l2_penalty_ratio=1.0, **parameters)[source]¶
Bases:
LinearRegressorPolynomial regression model.
- Parameters:
data (IODataset) – The learning dataset.
degree (int) – The polynomial degree.
transformer (TransformerType) –
The strategies to transform the variables. The values are instances of
Transformerwhile the keys are the names of either the variables or the groups of variables, e.g."inputs"or"outputs"in the case of the regression algorithms. If a group is specified, theTransformerwill be applied to all the variables of this group. IfIDENTITY, do not transform the variables.By default it is set to {}.
input_names (Iterable[str] | None) – The names of the input variables. If
None, consider all the input variables of the learning dataset.output_names (Iterable[str] | None) – The names of the output variables. If
None, consider all the output variables of the learning dataset.fit_intercept (bool) –
Whether to fit the intercept.
By default it is set to True.
penalty_level (float) –
The penalty level greater or equal to 0. If 0, there is no penalty.
By default it is set to 0.0.
l2_penalty_ratio (float) –
The penalty ratio related to the l2 regularization. If 1, the penalty is the Ridge penalty. If 0, this is the Lasso penalty. Between 0 and 1, the penalty is the ElasticNet penalty.
By default it is set to 1.0.
**parameters (float | int | str | bool | None) – The parameters of the machine learning algorithm.
- Raises:
ValueError – If the degree is lower than one.
- DataFormatters¶
alias of
RegressionDataFormatters
- get_coefficients(as_dict=False)[source]¶
Return the regression coefficients of the linear model.
- Parameters:
as_dict (bool) –
If
True, return the coefficients as a dictionary of Numpy arrays indexed by the names of the coefficients. Otherwise, return the coefficients as a Numpy array. For now the only valid value is False.By default it is set to False.
- Returns:
The regression coefficients of the linear model.
- Raises:
NotImplementedError – If the coefficients are required as a dictionary.
- Return type:
- get_intercept(as_dict=True)¶
Return the regression intercepts of the linear model.
- Parameters:
as_dict (bool) –
If
True, return the intercepts as a dictionary. Otherwise, return the intercepts as a numpy.arrayBy default it is set to True.
- Returns:
The regression intercepts of the linear model.
- Raises:
ValueError – If the coefficients are required as a dictionary even though the transformers change the variables dimensions.
- Return type:
- learn(samples=None, fit_transformers=True)¶
Train the machine learning algorithm from the learning dataset.
- load_algo(directory)[source]¶
Load a machine learning algorithm from a directory.
- Parameters:
directory (str | Path) – The path to the directory where the machine learning algorithm is saved.
- Return type:
None
- predict(input_data)¶
Predict output data from input data.
The user can specify these input data either as a NumPy array, e.g.
array([1., 2., 3.])or as a dictionary, e.g.{'a': array([1.]), 'b': array([2., 3.])}.If the numpy arrays are of dimension 2, their i-th rows represent the input data of the i-th sample; while if the numpy arrays are of dimension 1, there is a single sample.
The type of the output data and the dimension of the output arrays will be consistent with the type of the input data and the size of the input arrays.
- predict_jacobian(input_data)¶
Predict the Jacobians of the regression model at input_data.
The user can specify these input data either as a NumPy array, e.g.
array([1., 2., 3.])or as a dictionary, e.g.{'a': array([1.]), 'b': array([2., 3.])}.If the NumPy arrays are of dimension 2, their i-th rows represent the input data of the i-th sample; while if the NumPy arrays are of dimension 1, there is a single sample.
The type of the output data and the dimension of the output arrays will be consistent with the type of the input data and the size of the input arrays.
- Parameters:
input_data (DataType) – The input data.
- Returns:
The predicted Jacobian data.
- Return type:
NoReturn
- predict_raw(input_data)¶
Predict output data from input data.
- Parameters:
input_data (ndarray) – The input data with shape (n_samples, n_inputs).
- Returns:
The predicted output data with shape (n_samples, n_outputs).
- Return type:
ndarray
- to_pickle(directory=None, path='.', save_learning_set=False)¶
Save the machine learning algorithm.
- Parameters:
directory (str | None) – The name of the directory to save the algorithm.
path (str | Path) –
The path to parent directory where to create the directory.
By default it is set to “.”.
save_learning_set (bool) –
Whether to save the learning set or get rid of it to lighten the saved files.
By default it is set to False.
- Returns:
The path to the directory where the algorithm is saved.
- Return type:
- DEFAULT_TRANSFORMER: DefaultTransformerType = mappingproxy({'inputs': <gemseo.mlearning.transformers.scaler.min_max_scaler.MinMaxScaler object>, 'outputs': <gemseo.mlearning.transformers.scaler.min_max_scaler.MinMaxScaler object>})¶
The default transformer for the input and output data, if any.
- IDENTITY: Final[DefaultTransformerType] = mappingproxy({})¶
A transformer leaving the input and output variables as they are.
- LIBRARY: Final[str] = 'scikit-learn'¶
The name of the library of the wrapped machine learning algorithm.
- SHORT_ALGO_NAME: ClassVar[str] = 'PolyReg'¶
The short name of the machine learning algorithm, often an acronym.
Typically used for composite names, e.g.
f"{algo.SHORT_ALGO_NAME}_{dataset.name}"orf"{algo.SHORT_ALGO_NAME}_{discipline.name}".
- algo: Any¶
The interfaced machine learning algorithm.
- property learning_samples_indices: Sequence[int]¶
The indices of the learning samples used for the training.
- resampling_results: dict[str, tuple[Resampler, list[MLAlgo], list[ndarray] | ndarray]]¶
The resampler class names bound to the resampling results.
A resampling result is formatted as
(resampler, ml_algos, predictions)whereresampleris aResampler,ml_algosis the list of the associated machine learning algorithms built during the resampling stage andpredictionsare the predictions obtained with the latter.resampling_resultsstores only one resampling result per resampler type (e.g.,"CrossValidation","LeaveOneOut"and"Boostrap").
- transformer: dict[str, Transformer]¶
The strategies to transform the variables, if any.
The values are instances of
Transformerwhile the keys are the names of either the variables or the groups of variables, e.g. “inputs” or “outputs” in the case of the regression algorithms. If a group is specified, theTransformerwill be applied to all the variables of this group.