Note
Click here to download the full example code
Analytical test case # 3¶
In this example, we consider a simple optimization problem to illustrate algorithms interfaces and DOE libraries integration. Integer variables are used
Imports¶
from __future__ import absolute_import, division, print_function, unicode_literals
from future import standard_library
from numpy import sum as np_sum
from gemseo.algos.design_space import DesignSpace
from gemseo.algos.doe.doe_factory import DOEFactory
from gemseo.algos.opt_problem import OptimizationProblem
from gemseo.api import configure_logger, execute_post
from gemseo.core.function import MDOFunction
standard_library.install_aliases()
LOGGER = configure_logger()
Define the objective function¶
We define the objective function \(f(x)=\sum_{i=1}^dx_i\)
using a MDOFunction.
objective = MDOFunction(np_sum, name="f", expr="sum(x)")
Define the design space¶
Then, we define the DesignSpace with GEMSEO.
design_space = DesignSpace()
design_space.add_variable("x", 2, l_b=-5, u_b=5, var_type="integer")
Define the optimization problem¶
Then, we define the OptimizationProblem with GEMSEO.
problem = OptimizationProblem(design_space)
problem.objective = objective
Solve the optimization problem using a DOE algorithm¶
We can see this optimization problem as a trade-off and solve it by means of a design of experiments (DOE), e.g. full factorial design
DOEFactory().execute(problem, "fullfact", n_samples=11 ** 2)
Out:
Optimization result:
|_ Design variables: [-5. -5.]
|_ Objective function: -10.0
|_ Feasible solution: True
Post-process the results¶
execute_post(
problem, "ScatterPlotMatrix", variables_list=["x", "f"], save=False, show=True
)
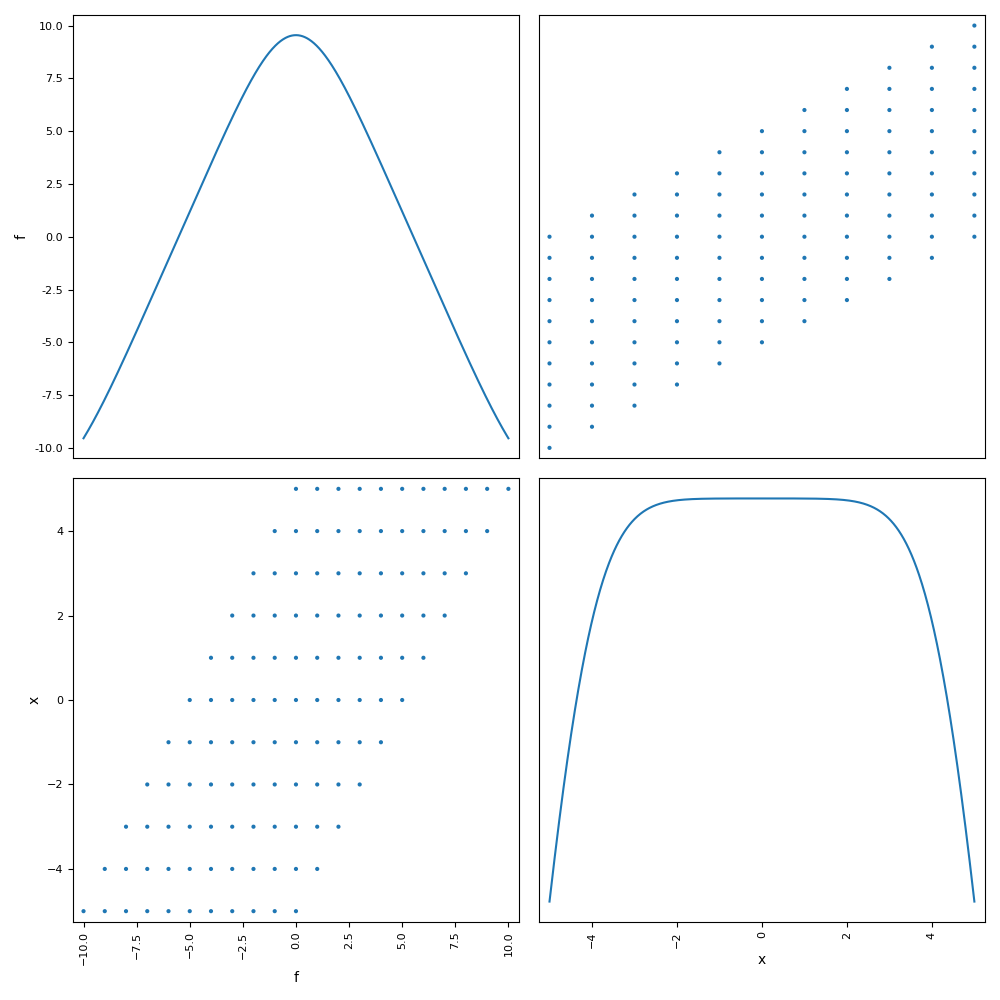
Out:
<gemseo.post.scatter_mat.ScatterPlotMatrix object at 0x7fc2990dff40>
Note that you can get all the optimization algorithms names:
algo_list = DOEFactory().algorithms
print("Available algorithms ", algo_list)
Out:
Available algorithms ['CustomDOE', 'DiagonalDOE', 'OT_SOBOL', 'OT_HASELGROVE', 'OT_REVERSE_HALTON', 'OT_HALTON', 'OT_FAURE', 'OT_AXIAL', 'OT_FACTORIAL', 'OT_MONTE_CARLO', 'OT_LHS', 'OT_LHSC', 'OT_RANDOM', 'OT_FULLFACT', 'OT_COMPOSITE', 'OT_SOBOL_INDICES', 'fullfact', 'ff2n', 'pbdesign', 'bbdesign', 'ccdesign', 'lhs']
Total running time of the script: ( 0 minutes 0.382 seconds)
