Scalable problem

We want to solve the Aerostructure MDO problem by means of the MDF formulation with a higher dimension for the sweep parameter. For that, we use the ScalableProblem class.

from __future__ import absolute_import, division, print_function, unicode_literals

from future import standard_library

from gemseo.api import configure_logger, create_discipline, create_scenario
from gemseo.problems.aerostructure.aerostructure_design_space import (
    AerostructureDesignSpace,
)
from gemseo.problems.scalable.problem import ScalableProblem

configure_logger()

standard_library.install_aliases()

Define the design problem

In a first step, we define the design problem in terms of objective function (to maximize or minimize), design variables (local and global) and constraints (equality and inequality).

design_variables = ["thick_airfoils", "thick_panels", "sweep"]
objective_function = "range"
eq_constraints = ["c_rf"]
ineq_constraints = ["c_lift"]
maximize_objective = True

Create the disciplinary datasets

Then, we create the disciplinary AbstractFullCache datasets based on a DiagonalDOE.

disciplines = create_discipline(["Aerodynamics", "Structure", "Mission"])
for discipline in disciplines:
    discipline.set_cache_policy(discipline.MEMORY_FULL_CACHE)
    design_space = AerostructureDesignSpace()
    design_space.filter(discipline.get_input_data_names())
    output = next(iter(discipline.get_output_data_names()))
    scenario = create_scenario(
        discipline, "DisciplinaryOpt", output, design_space, scenario_type="DOE"
    )
    scenario.execute({"algo": "DiagonalDOE", "n_samples": 10})

Instantiate a scalable problem

In a third stage, we instantiate a ScalableProblem from these disciplinary datasets and from the definition of the MDO problem. We also increase the dimension of the sweep parameter.

datasets = [discipline.cache for discipline in disciplines]
problem = ScalableProblem(
    datasets,
    design_variables,
    objective_function,
    eq_constraints,
    ineq_constraints,
    maximize_objective,
    sizes={"sweep": 2},
)
print(problem)

Out:

/home/docs/checkouts/readthedocs.org/user_builds/gemseo/conda/3.0.3/lib/python3.8/site-packages/scipy/interpolate/fitpack2.py:611: ComplexWarning: Casting complex values to real discards the imaginary part
  self._data = dfitpack.fpcurf0(x, y, k, w=w, xb=bbox[0],
MDO problem
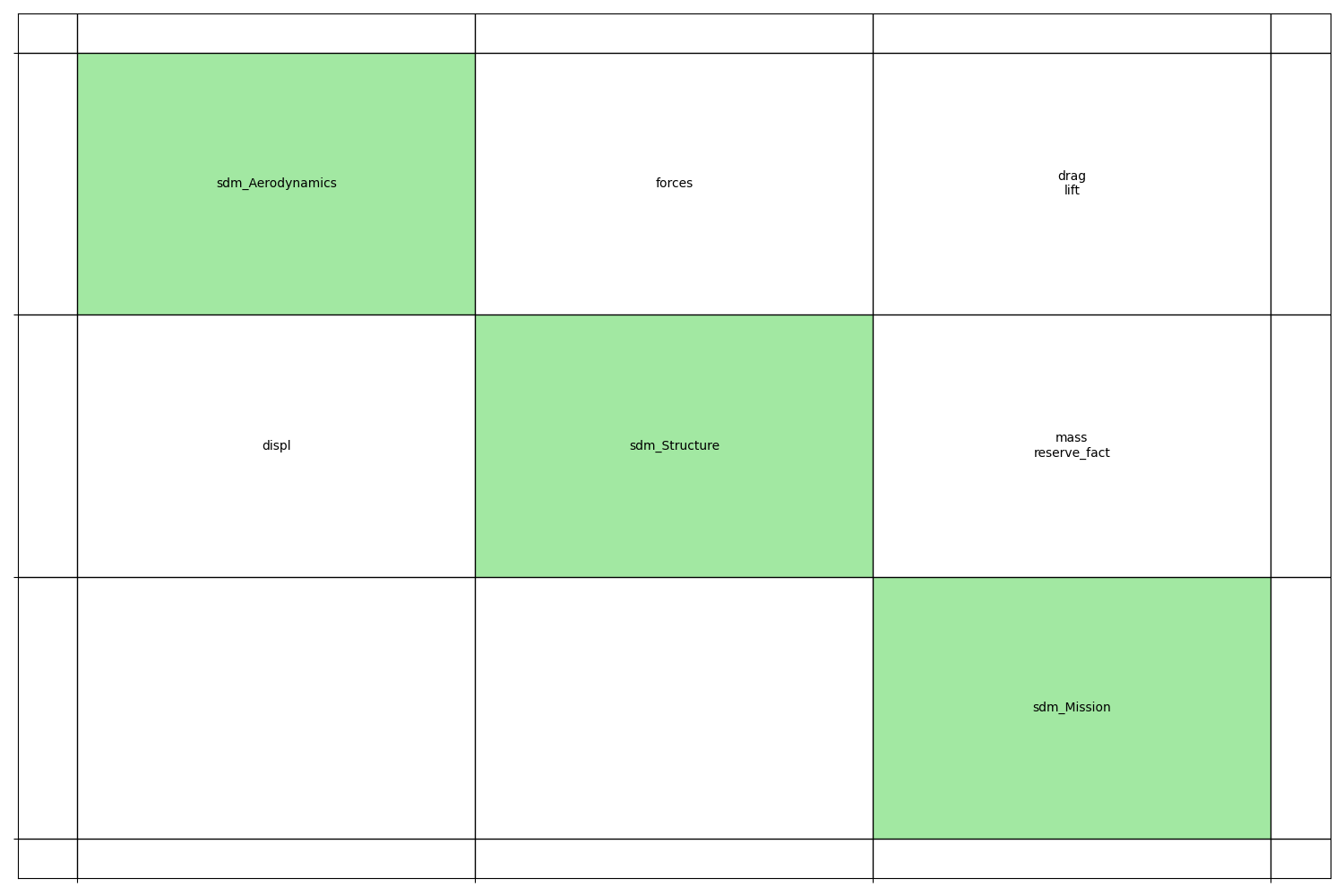
| Disciplines: Aerodynamics, Structure, Mission
| Design variables: thick_airfoils, thick_panels, sweep
| Objective function: range (to maximize)
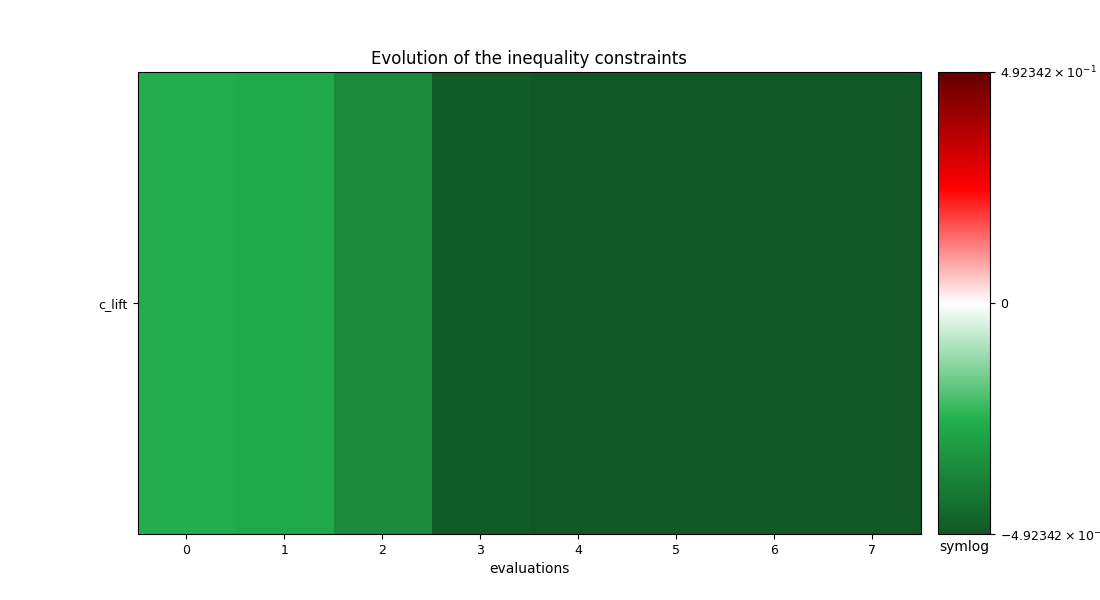
| Inequality constraints: c_lift
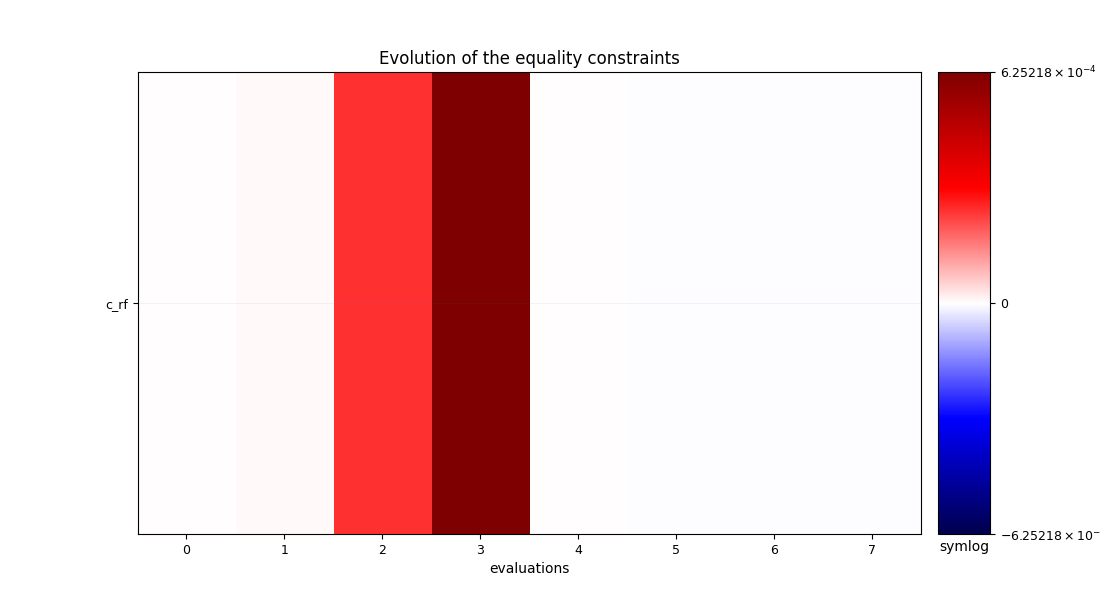
| Equality constraints: c_rf
| Sizes: sweep (2), thick_airfoils (1), displ (1), drag (1), forces (1), lift (1), thick_panels (1), mass (1), reserve_fact (1), range (1), c_lift (1), c_rf (1)

Note

We could also provide options to the ScalableModel objects by means of the constructor of ScalableProblem, e.g. fill_factor in the frame of the ScalableDiagonalModel. In this example, we use the standard ones.

Visualize the N2 chart

We can see the coupling between disciplines through this N2 chart:

problem.plot_n2_chart(save=False, show=True)

Create a MDO scenario

Lastly, we create a MDOScenario with the MDF formulation and start the optimization at equilibrium, thus ensuring the feasibility of the first iterate.

scenario = problem.create_scenario("MDF", start_at_equilibrium=True)

Once the scenario is created, we can execute it as any scenario. Here, we use the NLOPT_SLSQP optimization algorithm with no more than 100 iterations.

scenario.execute({"algo": "NLOPT_SLSQP", "max_iter": 100})

Out:

{'algo': 'NLOPT_SLSQP', 'max_iter': 100}

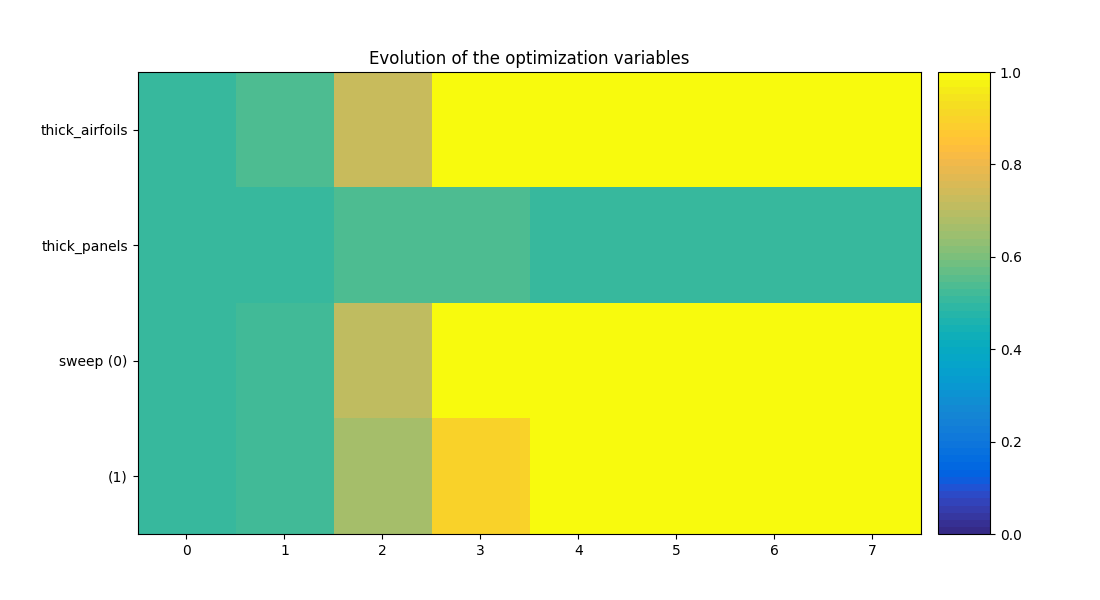
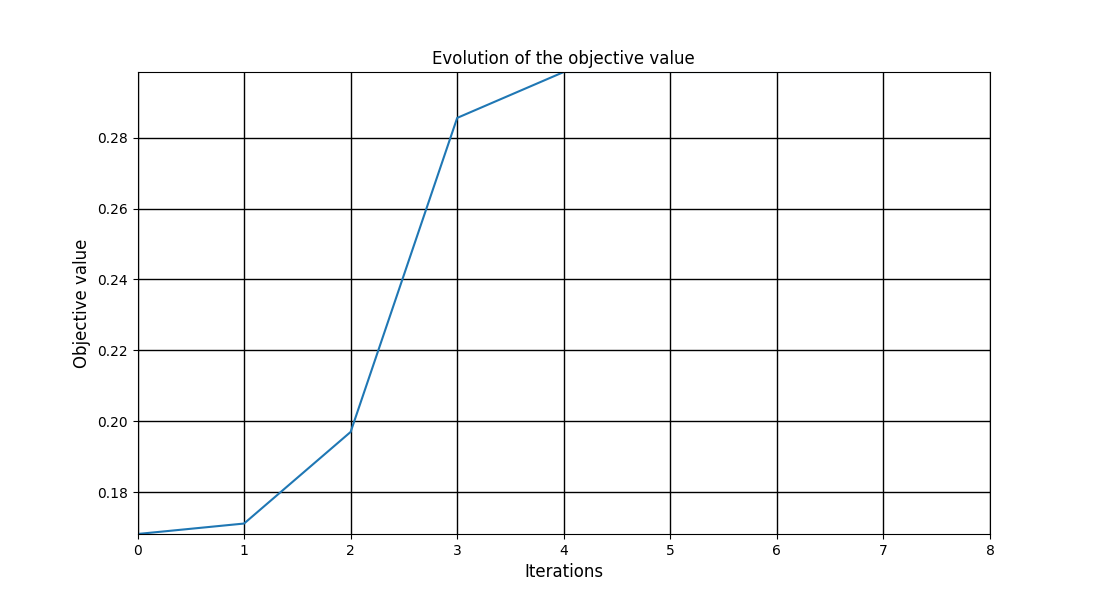
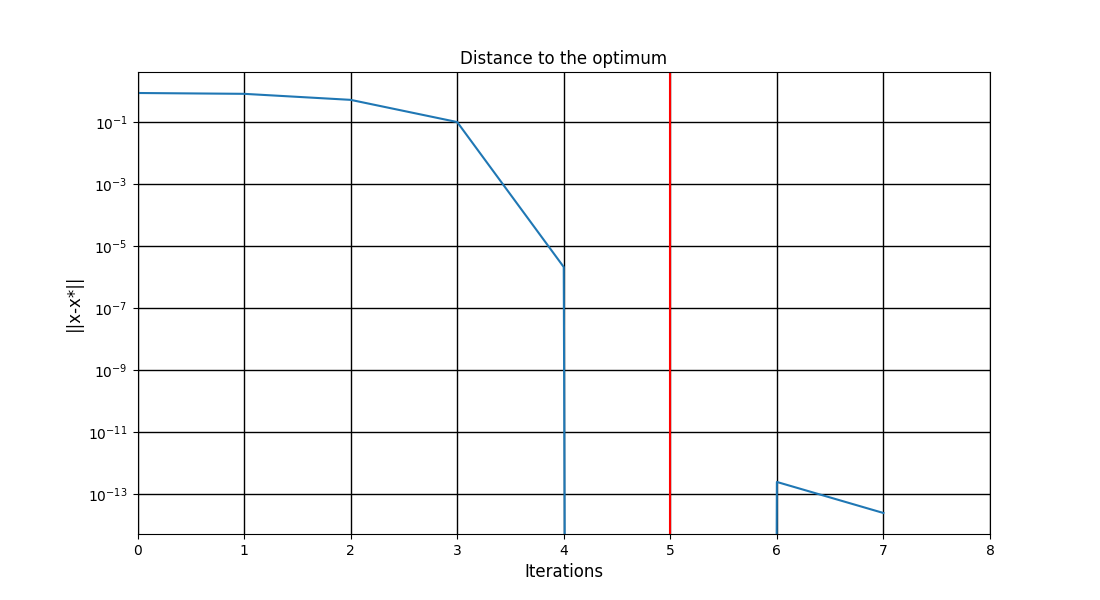
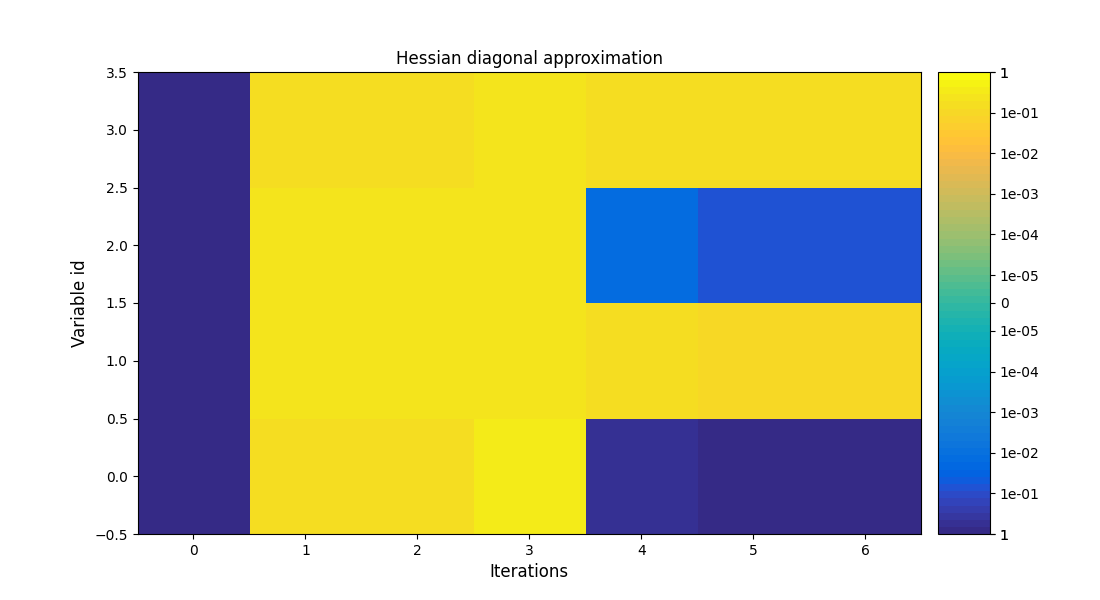
We can post-process the results. Here, we use the standard OptHistoryView.

scenario.post_process("OptHistoryView", save=False, show=True)

• 
• 
• 
• 
• 
• 

Out:

/home/docs/checkouts/readthedocs.org/user_builds/gemseo/conda/3.0.3/lib/python3.8/site-packages/gemseo/post/opt_history_view.py:312: UserWarning: FixedFormatter should only be used together with FixedLocator
  ax1.set_yticklabels(y_labels)
/home/docs/checkouts/readthedocs.org/user_builds/gemseo/conda/3.0.3/lib/python3.8/site-packages/gemseo/post/opt_history_view.py:716: MatplotlibDeprecationWarning: default base will change from np.e to 10 in 3.4.  To suppress this warning specify the base keyword argument.
  norm=SymLogNorm(linthresh=linthresh, vmin=-vmax, vmax=vmax),
/home/docs/checkouts/readthedocs.org/user_builds/gemseo/conda/3.0.3/lib/python3.8/site-packages/gemseo/post/opt_history_view.py:626: MatplotlibDeprecationWarning: default base will change from np.e to 10 in 3.4.  To suppress this warning specify the base keyword argument.
  norm=SymLogNorm(linthresh=1.0, vmin=-vmax, vmax=vmax),
/home/docs/checkouts/readthedocs.org/user_builds/gemseo/conda/3.0.3/lib/python3.8/site-packages/gemseo/post/opt_history_view.py:619: MatplotlibDeprecationWarning: Passing parameters norm and vmin/vmax simultaneously is deprecated since 3.3 and will become an error two minor releases later. Please pass vmin/vmax directly to the norm when creating it.
  im1 = ax1.imshow(

<gemseo.post.opt_history_view.OptHistoryView object at 0x7fc29e235c70>