Note
Click here to download the full example code
Scalable problem of Tedford and Martins, 2010¶
from __future__ import absolute_import, division, print_function, unicode_literals
from future import standard_library
from numpy import array
from numpy.random import rand
from gemseo.api import generate_n2_plot
from gemseo.problems.scalable.scalable_tm.core import (
TMParamSS,
TMParamSSPost,
TMScalableProblem,
TMScalableStudy,
)
from gemseo.problems.scalable.scalable_tm.design_space import TMDesignSpace
from gemseo.problems.scalable.scalable_tm.disciplines import TMDiscipline, TMSystem
standard_library.install_aliases()
Disciplines¶
We define two strongly coupled disciplines and a weakly coupled discipline, with:
2 shared design parameters,
2 local design parameters for the first discipline,
3 local design parameters for the second discipline,
3 coupling variables for the first discipline,
2 coupling variables for the second discipline.
sizes = {"x_shared": 2, "x_local_0": 2, "x_local_1": 3, "y_0": 3, "y_1": 2}
We use any values for the coefficients and the default values of the design parameters and coupling variables.
Strongly coupled disciplines¶
Here is the first strongly coupled discipline.
default_inputs = {
"x_shared": rand(sizes["x_shared"]),
"x_local_0": rand(sizes["x_local_0"]),
"y_1": rand(sizes["y_1"]),
}
index = 0
c_shared = rand(sizes["y_0"], sizes["x_shared"])
c_local = rand(sizes["y_0"], sizes["x_local_0"])
c_coupling = {"y_1": rand(sizes["y_0"], sizes["y_1"])}
disc0 = TMDiscipline(index, c_shared, c_local, c_coupling, default_inputs)
print(disc0.name)
print(disc0.get_input_data_names())
print(disc0.get_output_data_names())
TM_Discipline_0
dict_keys(['x_shared', 'x_local_0', 'y_1'])
dict_keys(['y_0'])
Here is the second one, strongly coupled with the first one.
default_inputs = {
"x_shared": rand(sizes["x_shared"]),
"x_local_1": rand(sizes["x_local_1"]),
"y_0": rand(sizes["y_0"]),
}
index = 1
c_shared = rand(sizes["y_1"], sizes["x_shared"])
c_local = rand(sizes["y_1"], sizes["x_local_1"])
c_coupling = {"y_0": rand(sizes["y_1"], sizes["y_0"])}
disc1 = TMDiscipline(index, c_shared, c_local, c_coupling, default_inputs)
print(disc1.name)
print(disc1.get_input_data_names())
print(disc1.get_output_data_names())
TM_Discipline_1
dict_keys(['x_shared', 'x_local_1', 'y_0'])
dict_keys(['y_1'])
Weakly coupled discipline¶
Here is the discipline weakly coupled to the previous ones.
c_constraint = [array([1.0, 2.0]), array([3.0, 4.0, 5.0])]
default_inputs = {
"x_shared": array([0.5]),
"y_0": array([2.0, 3.0]),
"y_1": array([4.0, 5.0, 6.0]),
}
system = TMSystem(c_constraint, default_inputs)
print(system.name)
print(system.get_input_data_names())
print(system.get_output_data_names())
TM_System
dict_keys(['x_shared', 'y_0', 'y_1'])
dict_keys(['obj', 'cstr_0', 'cstr_1'])
Coupling chart¶
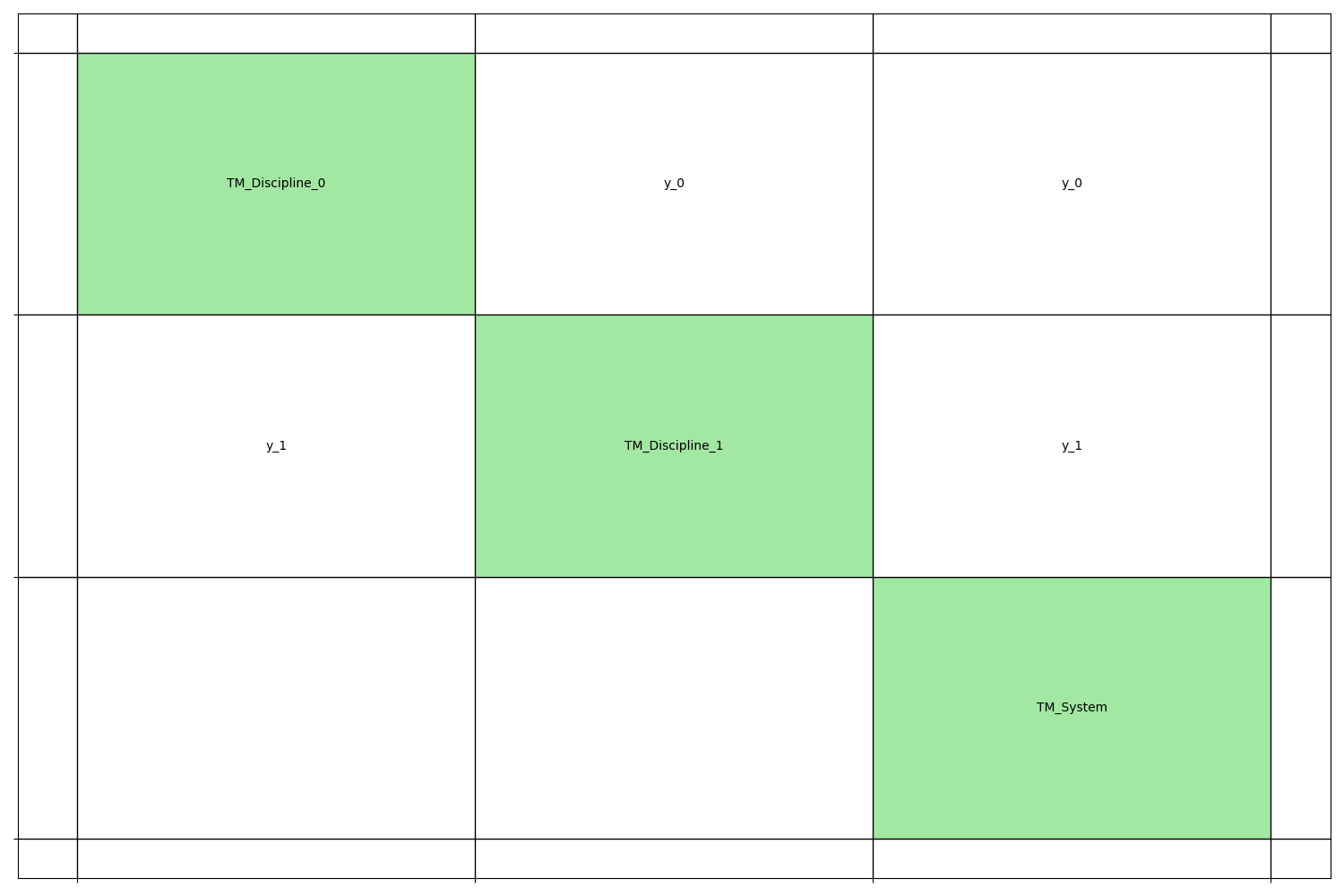
We can represent these three disciplines by means of a N2 chart.
generate_n2_plot([disc0, disc1, system], save=False, show=True)
Design space¶
We define the design space from the sizes of the shared design parameters, local parameters and coupling variables.
n_shared = sizes["x_shared"]
n_local = [sizes["x_local_0"], sizes["x_local_1"]]
n_coupling = [sizes["y_0"], sizes["y_1"]]
design_space = TMDesignSpace(n_shared, n_local, n_coupling)
print(design_space)
Design Space:
+-----------+-------------+-------+-------------+-------+
| name | lower_bound | value | upper_bound | type |
+-----------+-------------+-------+-------------+-------+
| x_local_0 | 0 | 0.5 | 1 | float |
| x_local_0 | 0 | 0.5 | 1 | float |
| x_local_1 | 0 | 0.5 | 1 | float |
| x_local_1 | 0 | 0.5 | 1 | float |
| x_local_1 | 0 | 0.5 | 1 | float |
| x_shared | 0 | 0.5 | 1 | float |
| x_shared | 0 | 0.5 | 1 | float |
| y_0 | 0 | 0.5 | 1 | float |
| y_0 | 0 | 0.5 | 1 | float |
| y_0 | 0 | 0.5 | 1 | float |
| y_1 | 0 | 0.5 | 1 | float |
| y_1 | 0 | 0.5 | 1 | float |
+-----------+-------------+-------+-------------+-------+
Scalable problem¶
We define a scalable problem based on two strongly coupled disciplines and a weakly one, with the following properties:
3 shared design parameters,
2 local design parameters for the first strongly coupled discipline,
2 coupling variables for the first strongly coupled discipline,
4 local design parameters for the second strongly coupled discipline,
3 coupling variables for the second strongly coupled discipline.
problem = TMScalableProblem(3, [2, 4], [2, 3])
print(problem)
print(problem.get_design_space())
print(problem.get_default_inputs())
Scalable problem
> TM_System
>> Inputs:
| x_shared (3)
| y_0 (2)
| y_1 (3)
>> Outputs:
| cstr_0 (2)
| cstr_1 (3)
| obj (1)
> TM_Discipline_0
>> Inputs:
| x_local_0 (2)
| x_shared (3)
| y_1 (3)
>> Outputs:
| y_0 (2)
> TM_Discipline_1
>> Inputs:
| x_local_1 (4)
| x_shared (3)
| y_0 (2)
>> Outputs:
| y_1 (3)
Design Space:
+-----------+-------------+-------+-------------+-------+
| name | lower_bound | value | upper_bound | type |
+-----------+-------------+-------+-------------+-------+
| x_local_0 | 0 | 0.5 | 1 | float |
| x_local_0 | 0 | 0.5 | 1 | float |
| x_local_1 | 0 | 0.5 | 1 | float |
| x_local_1 | 0 | 0.5 | 1 | float |
| x_local_1 | 0 | 0.5 | 1 | float |
| x_local_1 | 0 | 0.5 | 1 | float |
| x_shared | 0 | 0.5 | 1 | float |
| x_shared | 0 | 0.5 | 1 | float |
| x_shared | 0 | 0.5 | 1 | float |
| y_0 | 0 | 0.5 | 1 | float |
| y_0 | 0 | 0.5 | 1 | float |
| y_1 | 0 | 0.5 | 1 | float |
| y_1 | 0 | 0.5 | 1 | float |
| y_1 | 0 | 0.5 | 1 | float |
+-----------+-------------+-------+-------------+-------+
{'x_shared': array([0.5, 0.5, 0.5]), 'x_local_0': array([0.5, 0.5]), 'y_0': array([0.5, 0.5]), 'cstr_0': array([0.5]), 'x_local_1': array([0.5, 0.5, 0.5, 0.5]), 'y_1': array([0.5, 0.5, 0.5]), 'cstr_1': array([0.5])}
Scalable study¶
We define a scalable study based on two strongly coupled disciplines and a weakly one, with the following properties:
3 shared design parameters,
2 local design parameters for each strongly coupled discipline,
3 coupling variables for each strongly coupled discipline.
study = TMScalableStudy(n_disciplines=2, n_shared=3, n_local=2, n_coupling=3)
print(study)
Scalable study
> 2 disciplines
> 3 shared design parameters
> 2 local design parameters per discipline
> 3 coupling variables per discipline
Then, we run MDF and IDF formulations:
study.run_formulation("MDF")
study.run_formulation("IDF")
We can look at the result in the console:
print(study)
Scalable study
> 2 disciplines
> 3 shared design parameters
> 2 local design parameters per discipline
> 3 coupling variables per discipline
MDO formulations
> MDF
>> TM_System = 9 calls / 7 linearizations / 3.29e-03 seconds
>> TM_Discipline_0 = 132 calls / 7 linearizations / 2.19e-02 seconds
>> TM_Discipline_1 = 124 calls / 7 linearizations / 2.04e-02 seconds
>> mda = 7 calls / 7 linearizations / 2.68e-01 seconds
>> mdo_chain = 7 calls / 0 linearizations / 1.20e-01 seconds
>> sub_mda = 7 calls / 0 linearizations / 1.16e-01 seconds
>> scenario = 1 calls / 0 linearizations / 3.35e-01 seconds
> IDF
>> TM_System = 12 calls / 9 linearizations / 2.98e-03 seconds
>> TM_Discipline_0 = 12 calls / 9 linearizations / 2.19e-03 seconds
>> TM_Discipline_1 = 11 calls / 9 linearizations / 2.01e-03 seconds
>> mda = 0 calls / 0 linearizations / 0.00e+00 seconds
>> mdo_chain = 0 calls / 0 linearizations / 0.00e+00 seconds
>> sub_mda = 0 calls / 0 linearizations / 0.00e+00 seconds
>> scenario = 1 calls / 0 linearizations / 7.60e-02 seconds
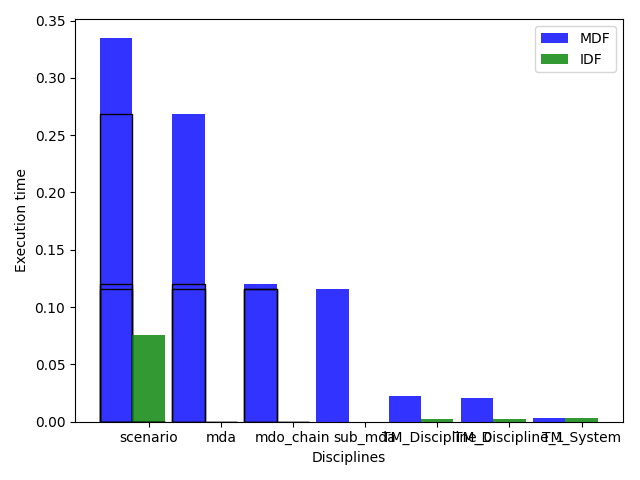
or plot the execution time:
study.plot_exec_time()
Parametric scalability study¶
We define a parametric scalability study based on two strongly coupled disciplines and a weakly one, with the following properties:
3 shared design parameters,
2 coupling variables for each strongly coupled discipline,
1, 5 or 25 local design parameters for each strongly coupled discipline,
study = TMParamSS(n_disciplines=2, n_shared=3, n_local=[1, 5, 25], n_coupling=2)
print(study)
Parametric scalable study
> 2 disciplines
> 3 shared design parameters
> 1, 5 or 25 local design parameters per discipline
> 2 coupling variables per discipline
Then, we run MDF and IDF formulations:
study.run_formulation("MDF")
study.run_formulation("IDF")
and save the results in a pickle file:
study.save("results.pkl")
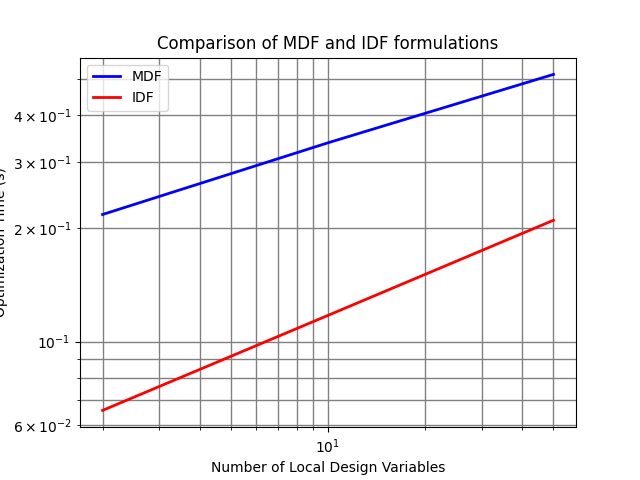
We can plot these results and compare MDF and IDF formulations in terms of execution time for different number of local design variables.
results = TMParamSSPost("results.pkl")
results.plot("Comparison of MDF and IDF formulations")
Total running time of the script: ( 0 minutes 0.000 seconds)
