Note
Click here to download the full example code
A from scratch example on the Sellar problem¶
Introduction¶
In this example, we will create a MDO scenario based on the Sellar’s problem
from scratch. Contrary to the |g| in ten minutes tutorial, all the disciplines will be implemented from scratch by
sub-classing the MDODiscipline class for each discipline of the
Sellar problem.
The Sellar problem¶
We will consider in this example the Sellar’s problem:
where the coupling variables are
and
and where the general constraints are
Imports¶
All the imports needed for the tutorials are performed here. Note that some of the imports are related to the Python 2/3 compatibility.
from __future__ import absolute_import, division, print_function, unicode_literals
from builtins import super
from math import exp, sqrt
from future import standard_library
from numpy import array, ones
from gemseo.algos.design_space import DesignSpace
from gemseo.api import configure_logger, create_scenario
from gemseo.core.discipline import MDODiscipline
configure_logger()
standard_library.install_aliases()
Create the disciplinary classes¶
In this section, we define the Sellar disciplines by sub-classing the
MDODiscipline class. For each class, the constructor and the _run
method are overriden:
In the constructor, the input and output grammar are created. They define which inputs and outputs variables are allowed at the discipline execution. The default inputs are also defined, in case of the user does not provide them at the discipline execution.
In the _run method is implemented the concrete computation of the discipline. The inputs data are fetch by using the
MDODiscipline.get_inputs_by_name()method. The returned Numpy arrays can then be used to compute the output values. They can then be stored in theMDODiscipline.local_datadictionary. If the discipline execution is successful.
Note that we do not define the Jacobians in the disciplines. In this example, we will approximate the derivatives using the finite differences method.
Create the SellarSystem class¶
class SellarSystem(MDODiscipline):
def __init__(self):
super(SellarSystem, self).__init__()
# Initialize the grammars to define inputs and outputs
self.input_grammar.initialize_from_data_names(["x", "z", "y_0", "y_1"])
self.output_grammar.initialize_from_data_names(["obj", "c_1", "c_2"])
# Default inputs define what data to use when the inputs are not
# provided to the execute method
self.default_inputs = {
"x": ones(1),
"z": array([4.0, 3.0]),
"y_0": ones(1),
"y_1": ones(1),
}
def _run(self):
# The run method defines what happens at execution
# ie how outputs are computed from inputs
x, z, y_0, y_1 = self.get_inputs_by_name(["x", "z", "y_0", "y_1"])
# The ouputs are stored here
self.local_data["obj"] = array([x[0] ** 2 + z[1] + y_0[0] ** 2 + exp(-y_1[0])])
self.local_data["c_1"] = array([1.0 - y_0[0] / 3.16])
self.local_data["c_2"] = array([y_1[0] / 24.0 - 1.0])
Create the Sellar1 class¶
class Sellar1(MDODiscipline):
def __init__(self):
super(Sellar1, self).__init__()
self.input_grammar.initialize_from_data_names(["x", "z", "y_1"])
self.output_grammar.initialize_from_data_names(["y_0"])
self.default_inputs = {
"x": ones(1),
"z": array([4.0, 3.0]),
"y_0": ones(1),
"y_1": ones(1),
}
def _run(self):
x, z, y_1 = self.get_inputs_by_name(["x", "z", "y_1"])
self.local_data["y_0"] = array([z[0] ** 2 + z[1] + x[0] - 0.2 * y_1[0]])
Create the Sellar2 class¶
class Sellar2(MDODiscipline):
def __init__(self):
super(Sellar2, self).__init__()
self.input_grammar.initialize_from_data_names(["z", "y_0"])
self.output_grammar.initialize_from_data_names(["y_1"])
self.default_inputs = {
"x": ones(1),
"z": array([4.0, 3.0]),
"y_0": ones(1),
"y_1": ones(1),
}
def _run(self):
z, y_0 = self.get_inputs_by_name(["z", "y_0"])
self.local_data["y_1"] = array([sqrt(y_0) + z[0] + z[1]])
Create and execute the scenario¶
Instantiate disciplines¶
We can now instantiate the disciplines and store the instances in a list which will be used below.
disciplines = [Sellar1(), Sellar2(), SellarSystem()]
Create the design space¶
In this section, we define the design space which will be used for the creation of the MDOScenario. Note that the coupling variables are defined in the design space. Indeed, as we are going to select the IDF formulation to solve the MDO scenario, the coupling variables will be unknowns of the optimization problem and consequently they have to be included in the design space. Conversely, it would not have been necessary to include them if we aimed to select a MDF formulation.
design_space = DesignSpace()
design_space.add_variable("x", 1, l_b=0.0, u_b=10.0, value=ones(1))
design_space.add_variable(
"z", 2, l_b=(-10, 0.0), u_b=(10.0, 10.0), value=array([4.0, 3.0])
)
design_space.add_variable("y_0", 1, l_b=-100.0, u_b=100.0, value=ones(1))
design_space.add_variable("y_1", 1, l_b=-100.0, u_b=100.0, value=ones(1))
Create the scenario¶
In this section, we build the MDO scenario which links the disciplines with the formulation, the design space and the objective function.
scenario = create_scenario(
disciplines, formulation="IDF", objective_name="obj", design_space=design_space
)
Add the constraints¶
Then, we have to set the design constraints
scenario.add_constraint("c_1", "ineq")
scenario.add_constraint("c_2", "ineq")
As previously mentioned, we are going to use finite differences to approximate the derivatives since the disciplines do not provide them.
scenario.set_differentiation_method("finite_differences", 1e-6)
Execute the scenario¶
Then, we execute the MDO scenario with the inputs of the MDO scenario as a dictionary. In this example, the gradient-based SLSQP optimizer is selected, with 10 iterations at maximum:
scenario.execute(input_data={"max_iter": 10, "algo": "SLSQP"})
Out:
{'max_iter': 10, 'algo': 'SLSQP'}
Post-process the scenario¶
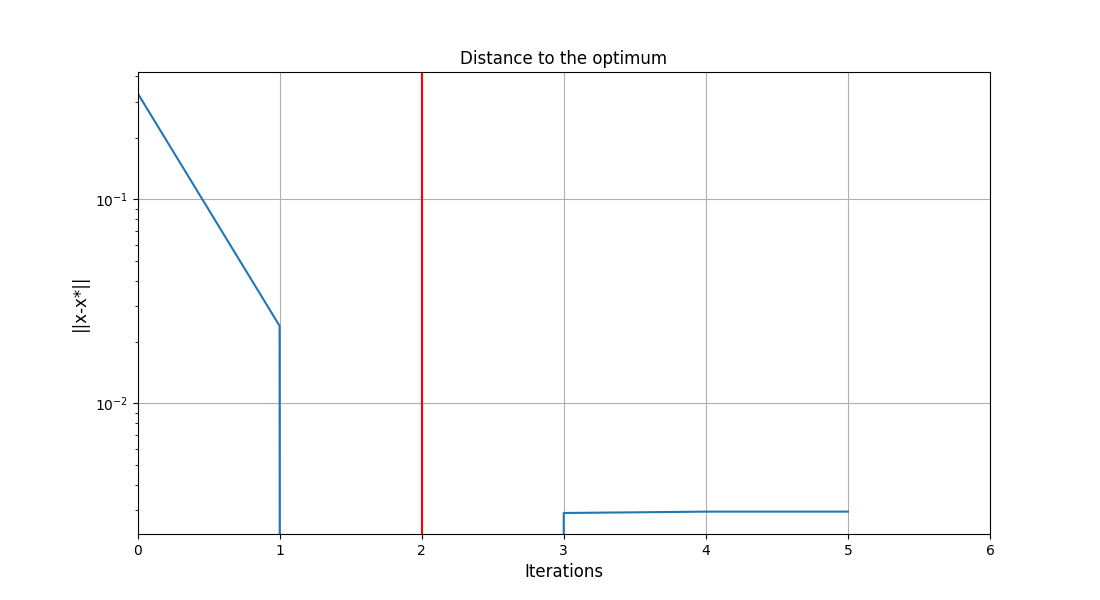
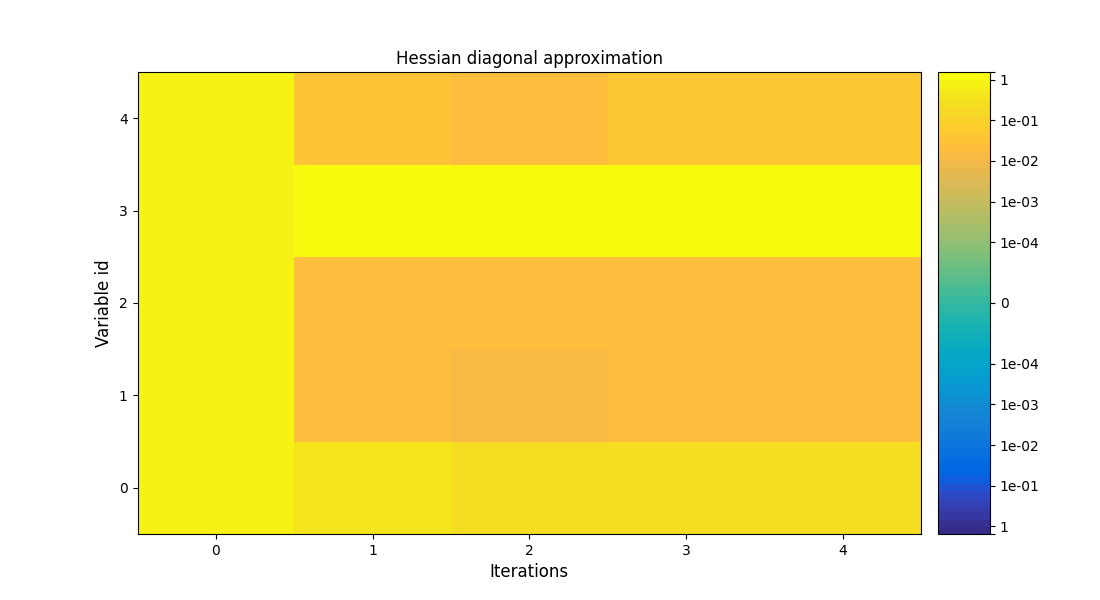
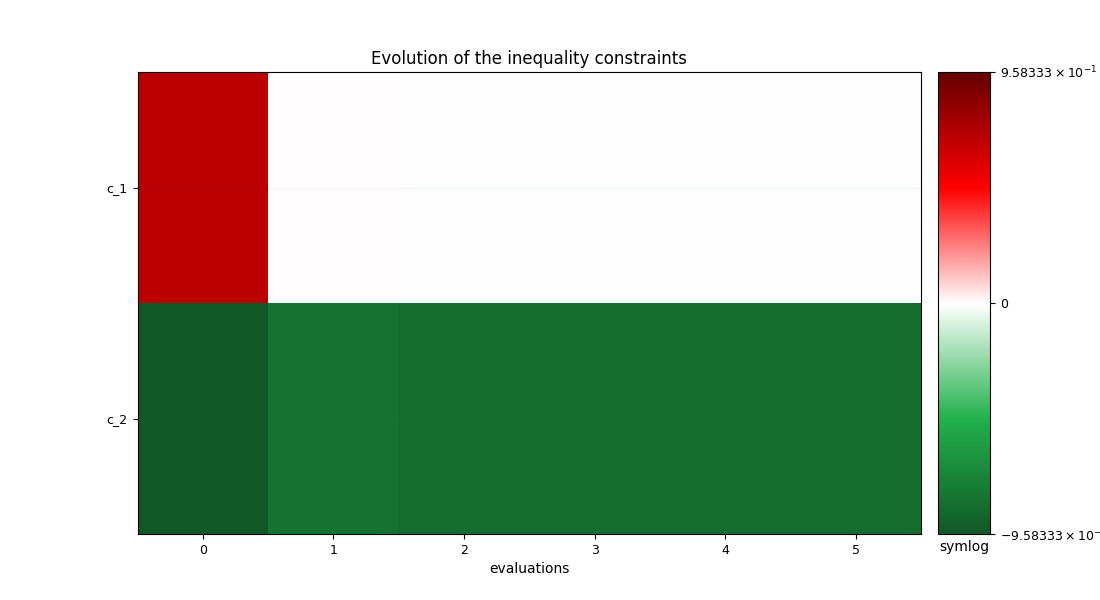
Finally, we can generate plots of the optimization history:
scenario.post_process("OptHistoryView", save=False, show=True)
Out:
/home/docs/checkouts/readthedocs.org/user_builds/gemseo/conda/3.0.3/lib/python3.8/site-packages/gemseo/post/opt_history_view.py:312: UserWarning: FixedFormatter should only be used together with FixedLocator
ax1.set_yticklabels(y_labels)
/home/docs/checkouts/readthedocs.org/user_builds/gemseo/conda/3.0.3/lib/python3.8/site-packages/gemseo/post/opt_history_view.py:716: MatplotlibDeprecationWarning: default base will change from np.e to 10 in 3.4. To suppress this warning specify the base keyword argument.
norm=SymLogNorm(linthresh=linthresh, vmin=-vmax, vmax=vmax),
/home/docs/checkouts/readthedocs.org/user_builds/gemseo/conda/3.0.3/lib/python3.8/site-packages/gemseo/post/opt_history_view.py:626: MatplotlibDeprecationWarning: default base will change from np.e to 10 in 3.4. To suppress this warning specify the base keyword argument.
norm=SymLogNorm(linthresh=1.0, vmin=-vmax, vmax=vmax),
/home/docs/checkouts/readthedocs.org/user_builds/gemseo/conda/3.0.3/lib/python3.8/site-packages/gemseo/post/opt_history_view.py:619: MatplotlibDeprecationWarning: Passing parameters norm and vmin/vmax simultaneously is deprecated since 3.3 and will become an error two minor releases later. Please pass vmin/vmax directly to the norm when creating it.
im1 = ax1.imshow(
<gemseo.post.opt_history_view.OptHistoryView object at 0x7fc29dafae20>
Total running time of the script: ( 0 minutes 1.042 seconds)