Note
Click here to download the full example code
Parametric scalable MDO problem - MDF¶
We define a scalable problem based on two strongly coupled disciplines and a weakly one, with the following properties:
3 shared design parameters,
2 local design parameters for the first strongly coupled discipline,
2 coupling variables for the first strongly coupled discipline,
4 local design parameters for the second strongly coupled discipline,
3 coupling variables for the second strongly coupled discipline.
We would like to solve this MDO problem by means of an MDF formulation.
from gemseo.api import configure_logger
from gemseo.api import create_scenario
from gemseo.api import generate_n2_plot
from gemseo.problems.scalable.parametric.problem import TMScalableProblem
from matplotlib import pyplot as plt
configure_logger()
Out:
<RootLogger root (INFO)>
Instantiation of the scalable problem¶
n_shared = 3
n_local = [2, 4]
n_coupling = [2, 3]
problem = TMScalableProblem(n_shared, n_local, n_coupling)
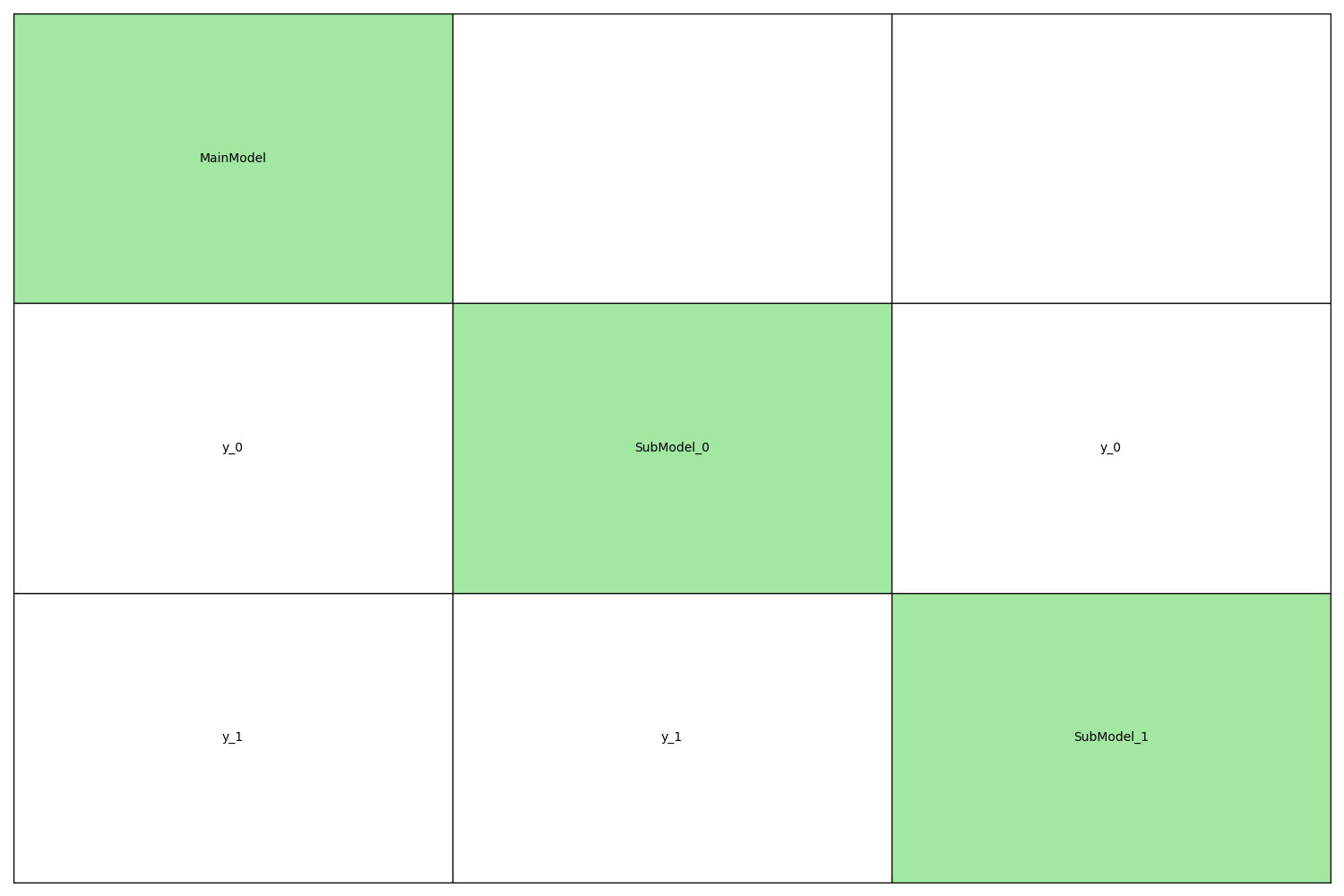
Display the coupling structure¶
generate_n2_plot(problem.disciplines, save=False, show=True)
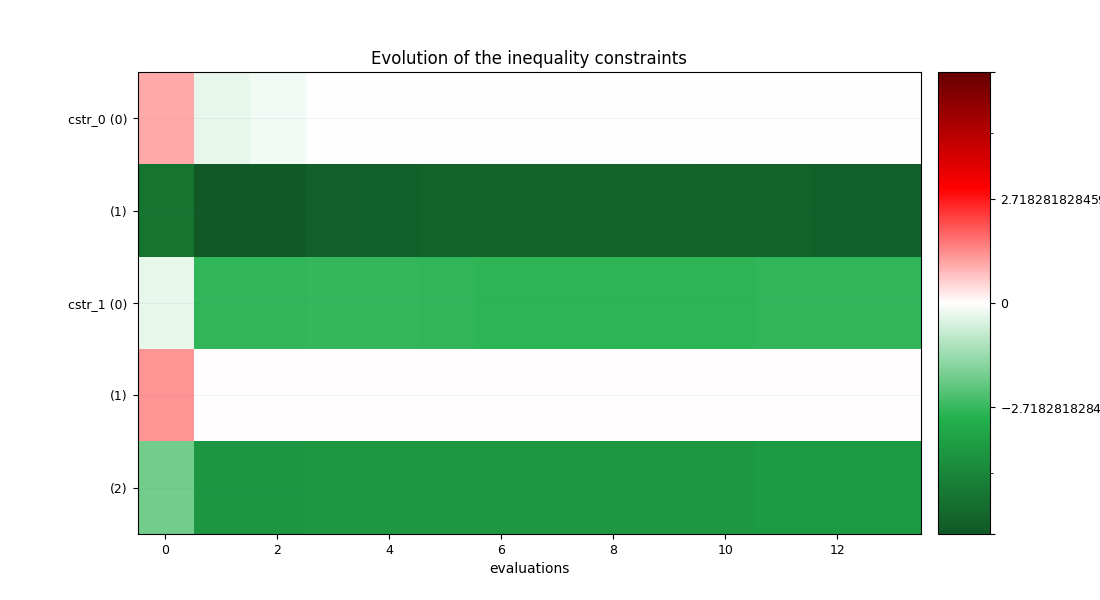
Solve the MDO using an MDF formulation¶
scenario = create_scenario(problem.disciplines, "MDF", "obj", problem.design_space)
scenario.add_constraint("cstr_0", "ineq")
scenario.add_constraint("cstr_1", "ineq")
scenario.execute({"algo": "NLOPT_SLSQP", "max_iter": 100})
Out:
INFO - 07:15:54:
INFO - 07:15:54: *** Start MDOScenario execution ***
INFO - 07:15:54: MDOScenario
INFO - 07:15:54: Disciplines: MainModel SubModel_0 SubModel_1
INFO - 07:15:54: MDO formulation: MDF
INFO - 07:15:54: Optimization problem:
INFO - 07:15:54: minimize obj(x_local_0, x_local_1, x_shared)
INFO - 07:15:54: with respect to x_local_0, x_local_1, x_shared
INFO - 07:15:54: subject to constraints:
INFO - 07:15:54: cstr_0(x_local_0, x_local_1, x_shared) <= 0.0
INFO - 07:15:54: cstr_1(x_local_0, x_local_1, x_shared) <= 0.0
INFO - 07:15:54: over the design space:
INFO - 07:15:54: | Parameter space |
INFO - 07:15:54: +-----------+-------------+-------+-------------+-------+----------------------+
INFO - 07:15:54: | name | lower_bound | value | upper_bound | type | Initial distribution |
INFO - 07:15:54: +-----------+-------------+-------+-------------+-------+----------------------+
INFO - 07:15:54: | x_local_0 | 0 | 0.5 | 1 | float | |
INFO - 07:15:54: | x_local_0 | 0 | 0.5 | 1 | float | |
INFO - 07:15:54: | x_local_1 | 0 | 0.5 | 1 | float | |
INFO - 07:15:54: | x_local_1 | 0 | 0.5 | 1 | float | |
INFO - 07:15:54: | x_local_1 | 0 | 0.5 | 1 | float | |
INFO - 07:15:54: | x_local_1 | 0 | 0.5 | 1 | float | |
INFO - 07:15:54: | x_shared | 0 | 0.5 | 1 | float | |
INFO - 07:15:54: | x_shared | 0 | 0.5 | 1 | float | |
INFO - 07:15:54: | x_shared | 0 | 0.5 | 1 | float | |
INFO - 07:15:54: +-----------+-------------+-------+-------------+-------+----------------------+
INFO - 07:15:54: Solving optimization problem with algorithm NLOPT_SLSQP:
INFO - 07:15:54: ... 0%| | 0/100 [00:00<?, ?it]
WARNING - 07:15:54: MDAJacobi has reached its maximum number of iterations but the normed residual 626.7567311166271 is still above the tolerance 1e-06.
INFO - 07:15:54: ... 2%|▏ | 2/100 [00:00<00:00, 680.96 it/sec]
WARNING - 07:15:54: MDAJacobi has reached its maximum number of iterations but the normed residual 857.8414771972733 is still above the tolerance 1e-06.
WARNING - 07:15:54: MDAJacobi has reached its maximum number of iterations but the normed residual 1221.6480671617337 is still above the tolerance 1e-06.
INFO - 07:15:54: ... 4%|▍ | 4/100 [00:00<00:00, 322.95 it/sec]
WARNING - 07:15:54: MDAJacobi has reached its maximum number of iterations but the normed residual 1386.3159812971933 is still above the tolerance 1e-06.
WARNING - 07:15:54: MDAJacobi has reached its maximum number of iterations but the normed residual 1736.3294618245698 is still above the tolerance 1e-06.
INFO - 07:15:54: ... 6%|▌ | 6/100 [00:00<00:00, 209.73 it/sec]
WARNING - 07:15:54: MDAJacobi has reached its maximum number of iterations but the normed residual 1805.5902082144773 is still above the tolerance 1e-06.
WARNING - 07:15:54: MDAJacobi has reached its maximum number of iterations but the normed residual 1805.4617138006554 is still above the tolerance 1e-06.
INFO - 07:15:54: ... 8%|▊ | 8/100 [00:00<00:00, 155.85 it/sec]
WARNING - 07:15:54: MDAJacobi has reached its maximum number of iterations but the normed residual 1801.736939733434 is still above the tolerance 1e-06.
WARNING - 07:15:55: MDAJacobi has reached its maximum number of iterations but the normed residual 1782.092029049005 is still above the tolerance 1e-06.
INFO - 07:15:55: ... 10%|█ | 10/100 [00:00<00:00, 123.90 it/sec]
WARNING - 07:15:55: MDAJacobi has reached its maximum number of iterations but the normed residual 1644.2104488173038 is still above the tolerance 1e-06.
WARNING - 07:15:55: MDAJacobi has reached its maximum number of iterations but the normed residual 907.4249280243517 is still above the tolerance 1e-06.
INFO - 07:15:55: ... 12%|█▏ | 12/100 [00:00<00:00, 102.86 it/sec]
WARNING - 07:15:55: MDAJacobi has reached its maximum number of iterations but the normed residual 728.104388120275 is still above the tolerance 1e-06.
WARNING - 07:15:55: MDAJacobi has reached its maximum number of iterations but the normed residual 726.426871749662 is still above the tolerance 1e-06.
INFO - 07:15:55: ... 14%|█▍ | 14/100 [00:01<00:00, 87.87 it/sec]
WARNING - 07:15:55: MDAJacobi has reached its maximum number of iterations but the normed residual 724.5329530118006 is still above the tolerance 1e-06.
INFO - 07:15:55: ... 15%|█▌ | 15/100 [00:01<00:01, 81.87 it/sec]
INFO - 07:15:55: Optimization result:
INFO - 07:15:55: Optimizer info:
INFO - 07:15:55: Status: None
INFO - 07:15:55: Message: Successive iterates of the objective function are closer than ftol_rel or ftol_abs. GEMSEO Stopped the driver
INFO - 07:15:55: Number of calls to the objective function by the optimizer: 15
INFO - 07:15:55: Solution:
INFO - 07:15:55: The solution is feasible.
INFO - 07:15:55: Objective: 0.6704638786393973
INFO - 07:15:55: Standardized constraints:
INFO - 07:15:55: cstr_0 = [-0.01693211 -5.62972098]
INFO - 07:15:55: cstr_1 = [-1.0547295 0. -1.8114265]
INFO - 07:15:55: +-------------------------------------------------------------------------------------------+
INFO - 07:15:55: | Parameter space |
INFO - 07:15:55: +-----------+-------------+--------------------+-------------+-------+----------------------+
INFO - 07:15:55: | name | lower_bound | value | upper_bound | type | Initial distribution |
INFO - 07:15:55: +-----------+-------------+--------------------+-------------+-------+----------------------+
INFO - 07:15:55: | x_local_0 | 0 | 0.5931064439648558 | 1 | float | |
INFO - 07:15:55: | x_local_0 | 0 | 1 | 1 | float | |
INFO - 07:15:55: | x_local_1 | 0 | 0 | 1 | float | |
INFO - 07:15:55: | x_local_1 | 0 | 0.9546530639347045 | 1 | float | |
INFO - 07:15:55: | x_local_1 | 0 | 0 | 1 | float | |
INFO - 07:15:55: | x_local_1 | 0 | 0 | 1 | float | |
INFO - 07:15:55: | x_shared | 0 | 0 | 1 | float | |
INFO - 07:15:55: | x_shared | 0 | 0 | 1 | float | |
INFO - 07:15:55: | x_shared | 0 | 0 | 1 | float | |
INFO - 07:15:55: +-----------+-------------+--------------------+-------------+-------+----------------------+
INFO - 07:15:55: *** End MDOScenario execution (time: 0:00:01.236933) ***
{'max_iter': 100, 'algo': 'NLOPT_SLSQP'}
Post-process the results¶
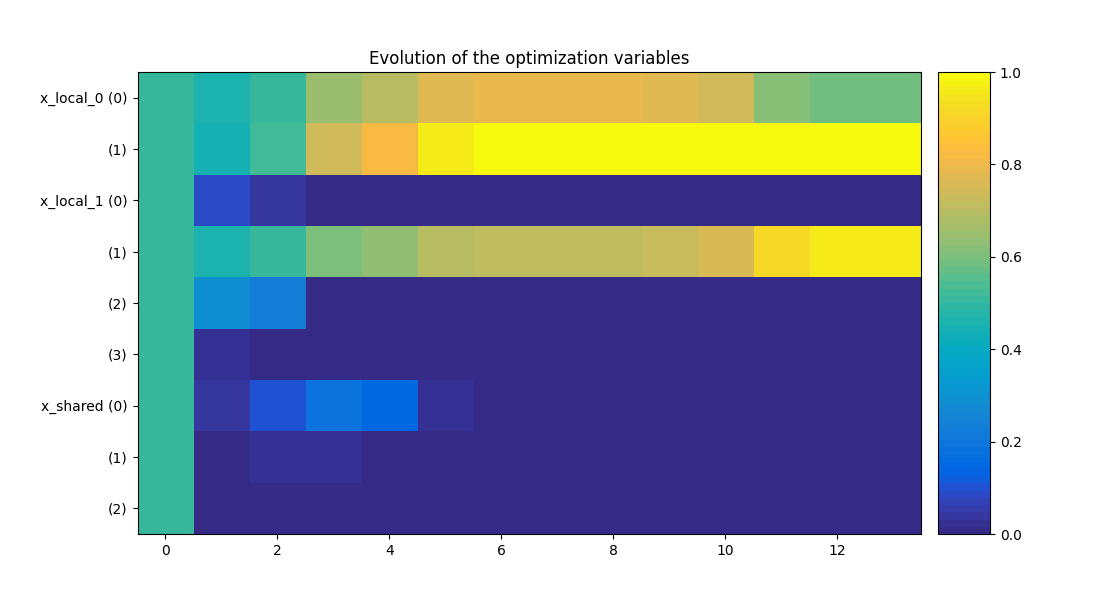
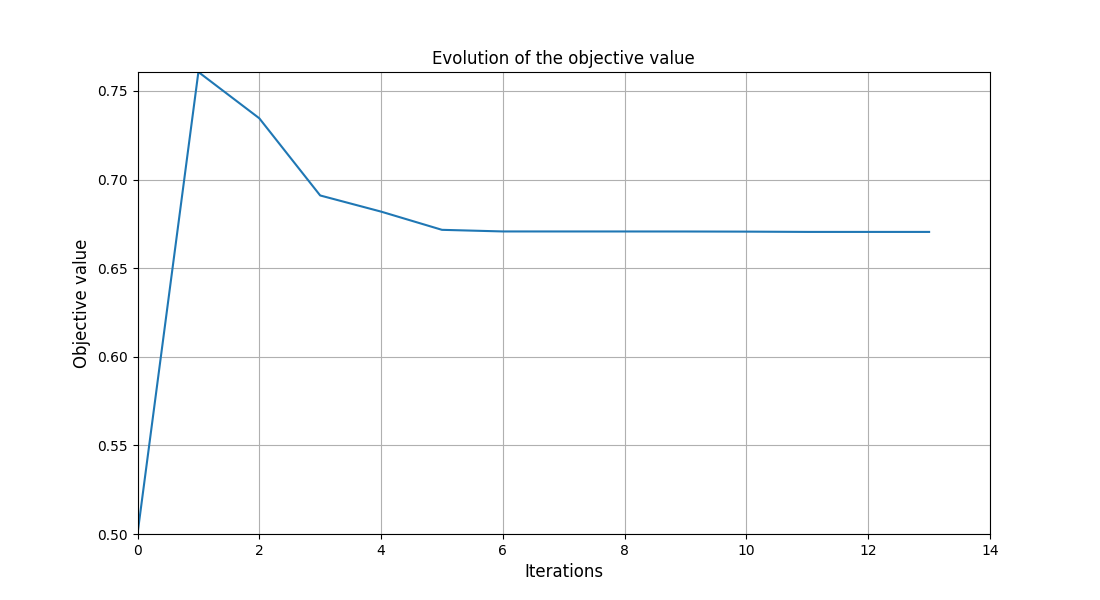
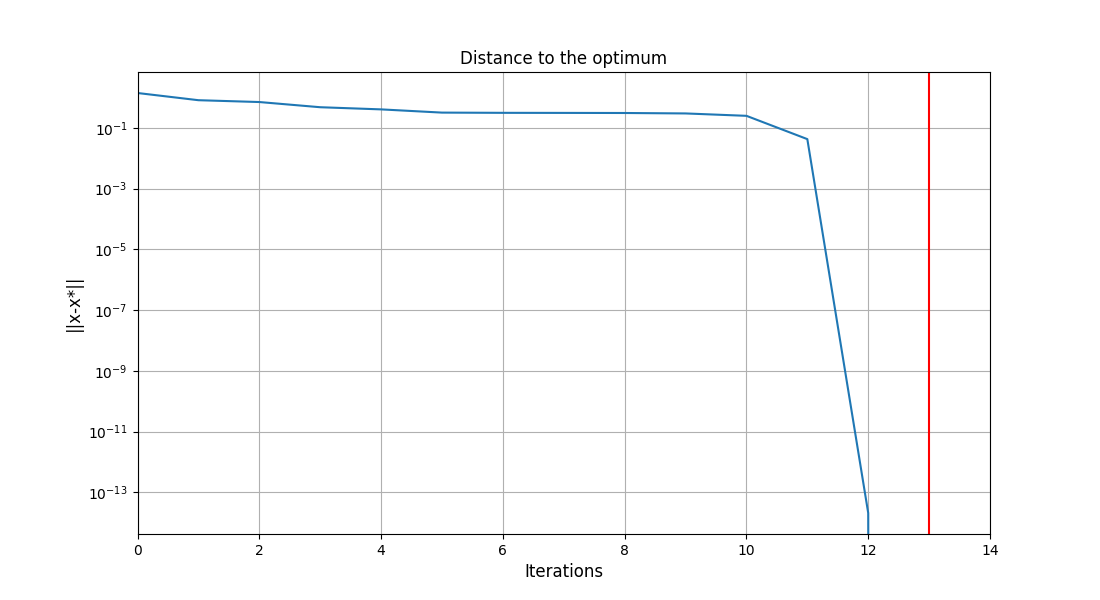
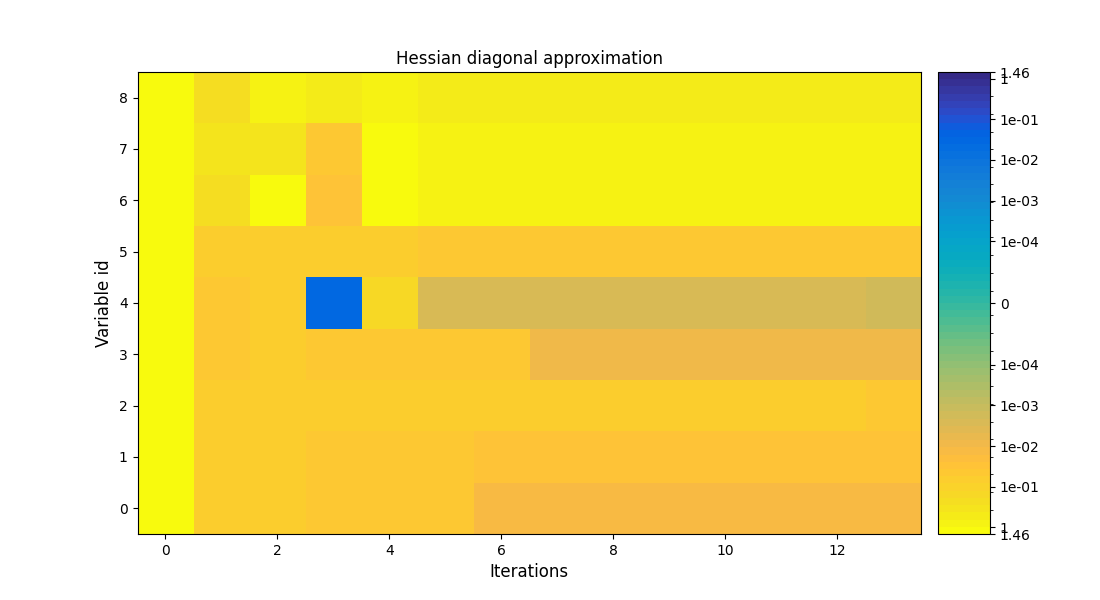
scenario.post_process("OptHistoryView", save=False, show=False)
# Workaround for HTML rendering, instead of ``show=True``
plt.show()
Total running time of the script: ( 0 minutes 2.499 seconds)