Note
Click here to download the full example code
Solve a 2D L-shape topology optimization problem¶
import matplotlib.pyplot as plt
from gemseo.api import configure_logger
from gemseo.api import create_scenario
from gemseo.problems.topo_opt.topopt_initialize import (
initialize_design_space_and_discipline_to,
)
from matplotlib import colors
configure_logger()
Out:
<RootLogger root (INFO)>
Setup the topology optimization problem¶
Define the target volume fractio:
volume_fraction = 0.3
Define the problem type:
problem_name = "L-Shape"
Define the number of elements in the x- and y- directions:
n_x = 25
n_y = 25
Define the full material Young’s modulus and Poisson’s ratio:
e0 = 1
nu = 0.3
Define the penalty of the SIMP approach:
penalty = 3
Define the minimum member size in the solution:
min_member_size = 1.5
Instantiate the DesignSpace and the disciplines:
design_space, disciplines = initialize_design_space_and_discipline_to(
problem=problem_name,
n_x=n_x,
n_y=n_y,
e0=e0,
nu=nu,
penalty=penalty,
min_member_size=min_member_size,
vf0=volume_fraction,
)
Solve the topology optimization problem¶
Generate a MDOScenario:
scenario = create_scenario(
disciplines,
formulation="DisciplinaryOpt",
objective_name="compliance",
design_space=design_space,
)
Add the volume fraction constraint to the scenario:
scenario.add_constraint("volume fraction", "ineq", value=volume_fraction)
Generate the XDSM
scenario.xdsmize()
Out:
INFO - 07:15:20: Generating HTML XDSM file in : xdsm.html
Execute the scenario
scenario.execute({"max_iter": 200, "algo": "NLOPT_MMA"})
Out:
INFO - 07:15:20:
INFO - 07:15:20: *** Start MDOScenario execution ***
INFO - 07:15:20: MDOScenario
INFO - 07:15:20: Disciplines: DensityFilter MaterialModelInterpolation FininiteElementAnalysis VolumeFraction
INFO - 07:15:20: MDO formulation: DisciplinaryOpt
INFO - 07:15:20: Optimization problem:
INFO - 07:15:20: minimize compliance(x)
INFO - 07:15:20: with respect to x
INFO - 07:15:20: subject to constraints:
INFO - 07:15:20: volume fraction(x) <= 0.3
INFO - 07:15:20: Solving optimization problem with algorithm NLOPT_MMA:
INFO - 07:15:20: ... 0%| | 0/200 [00:00<?, ?it]
INFO - 07:15:20: ... 1%| | 2/200 [00:00<00:00, 1956.06 it/sec]
INFO - 07:15:20: ... 2%|▎ | 5/200 [00:00<00:00, 861.65 it/sec]
INFO - 07:15:20: ... 4%|▍ | 8/200 [00:00<00:00, 547.03 it/sec]
INFO - 07:15:21: ... 6%|▌ | 11/200 [00:00<00:00, 400.46 it/sec]
INFO - 07:15:21: ... 7%|▋ | 14/200 [00:00<00:00, 317.42 it/sec]
INFO - 07:15:21: ... 8%|▊ | 17/200 [00:00<00:00, 263.79 it/sec]
INFO - 07:15:21: ... 10%|█ | 20/200 [00:00<00:00, 226.18 it/sec]
INFO - 07:15:21: ... 12%|█▏ | 23/200 [00:01<00:00, 198.04 it/sec]
INFO - 07:15:21: ... 13%|█▎ | 26/200 [00:01<00:00, 176.22 it/sec]
INFO - 07:15:21: ... 14%|█▍ | 29/200 [00:01<00:01, 158.82 it/sec]
INFO - 07:15:21: ... 16%|█▌ | 32/200 [00:01<00:01, 144.60 it/sec]
INFO - 07:15:22: ... 18%|█▊ | 35/200 [00:01<00:01, 132.89 it/sec]
INFO - 07:15:22: ... 19%|█▉ | 38/200 [00:01<00:01, 122.85 it/sec]
INFO - 07:15:22: ... 20%|██ | 41/200 [00:01<00:01, 114.17 it/sec]
INFO - 07:15:22: ... 22%|██▏ | 44/200 [00:01<00:01, 106.56 it/sec]
INFO - 07:15:22: ... 24%|██▎ | 47/200 [00:02<00:01, 99.96 it/sec]
INFO - 07:15:22: ... 25%|██▌ | 50/200 [00:02<00:01, 94.39 it/sec]
INFO - 07:15:22: ... 26%|██▋ | 53/200 [00:02<00:01, 89.29 it/sec]
INFO - 07:15:22: ... 28%|██▊ | 56/200 [00:02<00:01, 84.65 it/sec]
INFO - 07:15:23: ... 30%|██▉ | 59/200 [00:02<00:01, 80.50 it/sec]
INFO - 07:15:23: ... 31%|███ | 62/200 [00:02<00:01, 76.74 it/sec]
INFO - 07:15:23: ... 32%|███▎ | 65/200 [00:02<00:01, 73.30 it/sec]
INFO - 07:15:23: ... 34%|███▍ | 68/200 [00:02<00:01, 70.15 it/sec]
INFO - 07:15:23: ... 36%|███▌ | 71/200 [00:02<00:01, 67.22 it/sec]
INFO - 07:15:23: ... 37%|███▋ | 74/200 [00:03<00:01, 64.59 it/sec]
INFO - 07:15:23: ... 38%|███▊ | 77/200 [00:03<00:01, 62.18 it/sec]
INFO - 07:15:23: ... 40%|████ | 80/200 [00:03<00:02, 59.94 it/sec]
INFO - 07:15:24: ... 42%|████▏ | 83/200 [00:03<00:02, 57.87 it/sec]
INFO - 07:15:24: ... 43%|████▎ | 86/200 [00:03<00:02, 55.88 it/sec]
INFO - 07:15:24: ... 44%|████▍ | 89/200 [00:03<00:02, 54.07 it/sec]
INFO - 07:15:24: ... 46%|████▌ | 92/200 [00:03<00:02, 52.38 it/sec]
INFO - 07:15:24: ... 48%|████▊ | 95/200 [00:03<00:02, 50.80 it/sec]
INFO - 07:15:24: ... 49%|████▉ | 98/200 [00:04<00:02, 49.31 it/sec]
INFO - 07:15:24: ... 50%|█████ | 101/200 [00:04<00:02, 47.91 it/sec]
INFO - 07:15:24: ... 52%|█████▏ | 104/200 [00:04<00:02, 46.57 it/sec]
INFO - 07:15:24: ... 54%|█████▎ | 107/200 [00:04<00:02, 45.30 it/sec]
INFO - 07:15:25: ... 55%|█████▌ | 110/200 [00:04<00:02, 44.10 it/sec]
INFO - 07:15:25: ... 56%|█████▋ | 113/200 [00:04<00:02, 42.96 it/sec]
INFO - 07:15:25: ... 58%|█████▊ | 116/200 [00:04<00:02, 41.87 it/sec]
INFO - 07:15:25: ... 60%|█████▉ | 119/200 [00:04<00:01, 40.84 it/sec]
INFO - 07:15:25: ... 61%|██████ | 122/200 [00:05<00:01, 39.87 it/sec]
INFO - 07:15:25: ... 62%|██████▎ | 125/200 [00:05<00:01, 38.93 it/sec]
INFO - 07:15:25: ... 64%|██████▍ | 128/200 [00:05<00:01, 38.04 it/sec]
INFO - 07:15:25: ... 64%|██████▍ | 129/200 [00:05<00:01, 37.72 it/sec]
INFO - 07:15:25: Optimization result:
INFO - 07:15:25: Optimizer info:
INFO - 07:15:25: Status: None
INFO - 07:15:25: Message: Successive iterates of the objective function are closer than ftol_rel or ftol_abs. GEMSEO Stopped the driver
INFO - 07:15:25: Number of calls to the objective function by the optimizer: 129
INFO - 07:15:25: Solution:
INFO - 07:15:25: The solution is feasible.
INFO - 07:15:25: Objective: 151.62873248988768
INFO - 07:15:25: Standardized constraints:
INFO - 07:15:25: volume fraction - 0.3 = 1.0969287427831098e-06
INFO - 07:15:25: *** End MDOScenario execution (time: 0:00:05.316237) ***
{'max_iter': 200, 'algo': 'NLOPT_MMA'}
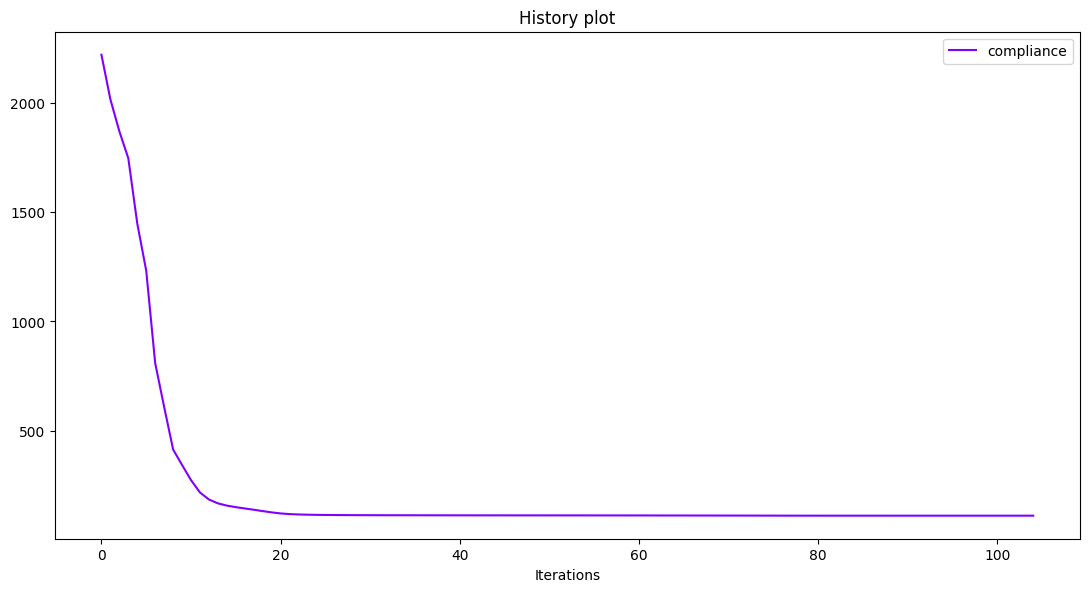
Results¶
Post-process the optimization history:
scenario.post_process(
"BasicHistory",
variable_names=["compliance"],
save=True,
show=False,
file_name=problem_name + "_history.png",
)
Out:
<gemseo.post.basic_history.BasicHistory object at 0x7f28f0e720d0>
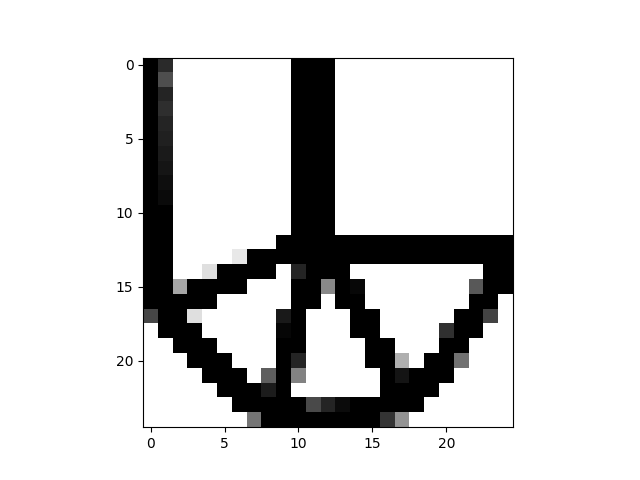
Plot the solution
plt.ion() # Ensure that redrawing is possible
fig, ax = plt.subplots()
im = ax.imshow(
-scenario.optimization_result.x_opt.reshape((n_x, n_y)).T,
cmap="gray",
interpolation="none",
norm=colors.Normalize(vmin=-1, vmax=0),
)
fig.show()
im.set_array(-scenario.optimization_result.x_opt.reshape((n_x, n_y)).T)
fig.canvas.draw()
plt.savefig(problem_name + "_solution.png")
Total running time of the script: ( 0 minutes 5.832 seconds)
