Probability distribution¶
The package distributions¶
Capabilities to create and manipulate probability distributions.
This package contains:
an abstract class
Distributionto define the concept of probability distribution,an abstract class
ComposedDistributionto define the concept of joint probability distribution by composing several instances ofDistribution,a factory
DistributionFactoryto create instances ofDistribution,concrete classes implementing these abstracts concepts, by interfacing:
the OpenTURNS library:
OTDistributionandOTComposedDistribution,the Scipy library:
SPDistributionandSPComposedDistribution.
Lastly, the class OTDistributionFitter offers the possibility
to fit an OTDistribution from data based on OpenTURNS.
The base class Distribution¶
Abstract class defining the concept of probability distribution.
Overview¶
The abstract Distribution class implements the concept of
probability distribution,
which is a mathematical function giving the probabilities of occurrence
of different possible outcomes of a random variable for an experiment.
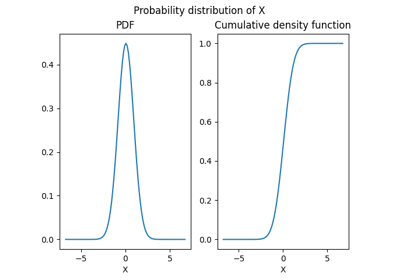
The normal distribution
with its famous bell curve is a well-known example of probability distribution.
See also
This abstract class is enriched by concrete ones,
such as OTDistribution interfacing the OpenTURNS probability distributions
and SPDistribution interfacing the SciPy probability distributions.
Construction¶
The Distribution of a given uncertain variable is built
from a recognized distribution name (e.g. ‘Normal’ for OpenTURNS or ‘norm’ for SciPy),
a variable dimension, a set of parameters
and optionally a standard representation of these parameters.
Capabilities¶
From a Distribution, we can easily get statistics,
such as Distribution.mean,
Distribution.standard_deviation. We can also get the
numerical Distribution.range and
mathematical Distribution.support.
Note
We call mathematical support the set of values that the random variable can take in theory, e.g. \(]-\infty,+\infty[\) for a Gaussian variable, and numerical range the set of values that it can can take in practice, taking into account the values rounded to zero double precision. Both support and range are described in terms of lower and upper bounds
We can also evaluate the cumulative density function
(Distribution.compute_cdf())
for the different marginals of the random variable,
as well as the inverse cumulative density function
(Distribution.compute_inverse_cdf()). We can plot them,
either for a given marginal (Distribution.plot())
or for all marginals (Distribution.plot_all()).
Lastly, we can compute realizations of the random variable
by means of the Distribution.compute_samples() method.
- class gemseo.uncertainty.distributions.distribution.Distribution(variable, interfaced_distribution, parameters, dimension=1, standard_parameters=None)[source]
Probability distribution related to a random variable.
The dimension of the random variable can be greater than 1. In this case, the same distribution is applied to all components of the random variable under the hypothesis that these components are stochastically independent.
The string representation of a distribution interfacing a distribution called
'MyDistribution'with parameters(2,3)is ‘MyDistribution(2, 3)` if no standard parameters are passed. If the standard parameters are{a: 2, b: 3}(resp.{a_inv: 2, b: 3}), then the standard representation is: ‘MyDistribution(a=2, b=3)` (resp. ‘MyDistribution(a_inv=0.5, b=3)`) Standard parameters are useful to redefine the name of the parameters. For example, some exponential distributions consider the notion of rate while other ones consider the notion of scale, which is the inverse of the rate… even in the background, the distribution is the same!- Parameters
variable (str) – The name of the random variable.
interfaced_distribution (str) – The name of the probability distribution, typically the name of a class wrapped from an external library, such as ‘Normal’ for OpenTURNS or ‘norm’ for SciPy.
parameters (ParametersType) – The parameters of the class related to distribution.
dimension (int) –
The dimension of the random variable.
By default it is set to 1.
standard_parameters (StandardParametersType | None) –
The standard representation of the parameters of the probability distribution.
By default it is set to None.
- Return type
None
- compute_cdf(vector)[source]
Evaluate the cumulative density function (CDF).
Evaluate the CDF of the components of the random variable for a given realization of this random variable.
- Parameters
vector (Iterable[float]) – A realization of the random variable.
- Returns
The CDF values of the components of the random variable.
- Return type
- compute_inverse_cdf(vector)[source]
Evaluate the inverse of the cumulative density function (ICDF).
- Parameters
vector (Iterable[float]) – A vector of values comprised between 0 and 1 whose length is equal to the dimension of the random variable.
- Returns
The ICDF values of the components of the random variable.
- Return type
- compute_samples(n_samples=1)[source]
Sample the random variable.
- Parameters
n_samples (int) –
The number of samples.
By default it is set to 1.
- Returns
The samples of the random variable,
The number of columns is equal to the dimension of the variable and the number of lines is equal to the number of samples.
- Return type
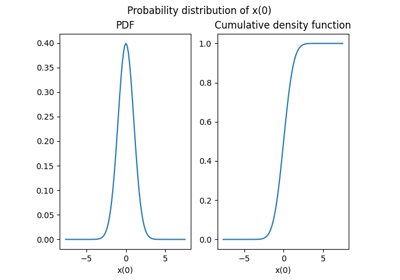
- plot(index=0, show=True, save=False, file_path=None, directory_path=None, file_name=None, file_extension=None)[source]
Plot both probability and cumulative density functions for a given component.
- Parameters
index (int) –
The index of a component of the random variable.
By default it is set to 0.
save (bool) –
If True, save the figure.
By default it is set to False.
show (bool) –
If True, display the figure.
By default it is set to True.
file_path (str | Path | None) –
The path of the file to save the figures. If the extension is missing, use
file_extension. If None, create a file path fromdirectory_path,file_nameandfile_extension.By default it is set to None.
directory_path (str | Path | None) –
The path of the directory to save the figures. If None, use the current working directory.
By default it is set to None.
file_name (str | None) –
The name of the file to save the figures. If None, use a default one generated by the post-processing.
By default it is set to None.
file_extension (str | None) –
A file extension, e.g. ‘png’, ‘pdf’, ‘svg’, … If None, use a default file extension.
By default it is set to None.
- Returns
The figure.
- Return type
Figure
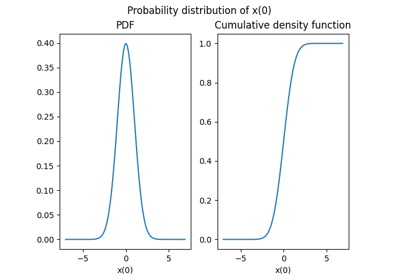
- plot_all(show=True, save=False, file_path=None, directory_path=None, file_name=None, file_extension=None)[source]
Plot both probability and cumulative density functions for all components.
- Parameters
save (bool) –
If True, save the figure.
By default it is set to False.
show (bool) –
If True, display the figure.
By default it is set to True.
file_path (str | Path | None) –
The path of the file to save the figures. If the extension is missing, use
file_extension. If None, create a file path fromdirectory_path,file_nameandfile_extension.By default it is set to None.
directory_path (str | Path | None) –
The path of the directory to save the figures. If None, use the current working directory.
By default it is set to None.
file_name (str | None) –
The name of the file to save the figures. If None, use a default one generated by the post-processing.
By default it is set to None.
file_extension (str | None) –
A file extension, e.g. ‘png’, ‘pdf’, ‘svg’, … If None, use a default file extension.
By default it is set to None.
- Returns
The figures.
- Return type
list[Figure]
- dimension: int
The number of dimensions of the random variable.
- distribution: type
The probability distribution of the random variable.
- distribution_name: str
The name of the probability distribution.
- math_lower_bound: ndarray
The mathematical lower bound of the random variable.
- math_upper_bound: ndarray
The mathematical upper bound of the random variable.
- property mean: numpy.ndarray
The analytical mean of the random variable.
- num_lower_bound: ndarray
The numerical lower bound of the random variable.
- num_upper_bound: ndarray
The numerical upper bound of the random variable.
- property range: list[numpy.ndarray]
The numerical range.
The numerical range is the interval defined by the lower and upper bounds numerically reachable by the random variable.
Here, the numerical range of the random variable is defined by one array for each component of the random variable, whose first element is the lower bound of this component while the second one is its upper bound.
- property standard_deviation: numpy.ndarray
The analytical standard deviation of the random variable.
- standard_parameters: dict[str, str] | None
The standard representation of the parameters of the distribution, used for its string representation.
- property support: list[numpy.ndarray]
The mathematical support.
The mathematical support is the interval defined by the theoretical lower and upper bounds of the random variable.
Here, the mathematical range of the random variable is defined by one array for each component of the random variable, whose first element is the lower bound of this component while the second one is its upper bound.
- transformation: str
The transformation applied to the random variable, e.g. ‘sin(x)’.
- variable_name: str
The name of the random variable.