Topology optimization

In these examples, 2D topology optimization problems are solved thanks to GEMSEO.

Topology optimization aims at finding the “best” material layout withing a given design space. It is especially useful in preliminary design phases when one only knows a component of the operating conditions and wants to find good design candidates achieving stiffer structures within a given mass budget. The formulation adopted in these examples is the Solid Isotropic Material with Penalization (SIMP) [1] approach.

The examples are the same from MATLAB and Python implementations described in [2] and [3] .

Problem Formulation

Given a 2D design space with loads and boundary conditions, let us take the example of an MBB structure:

First, the solid design space is meshed with 2D bi-linear squared finite elements. All the examples proposed here consider rectangular domains. This means that one only needs to define the number of elements in horizontal (x) and vertical (y) direction.

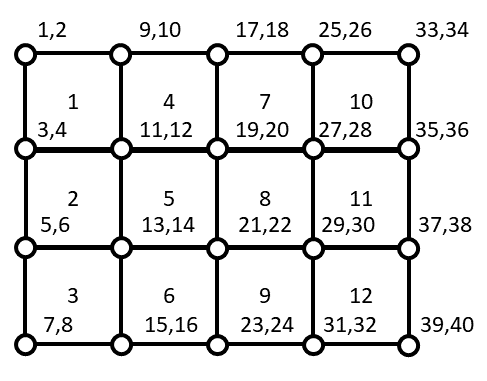
In the above figure it is possible to find the element and degree of freedoms numbering convention adopted for a 4x3 finite element mesh. What gives a very large design freedom to topology optimization is that a design variable \(x \in \{0,1\}^N\) is associated with each finite element. These variables are equal to 0 when the finite element is void and equal to 1 when the finite element is filled with solid material. In order to use the convergence rate of the gradient-based optimization solvers, the design variable are relaxed \(x \in [0,1]^N\). To enforce a discrete solution at convergence, the intermediate valuess of the design variables are penalized using the SIMP approach that introduces a power low relationship between the local material density and the Young’s modulus. In order to avoid numerical difficulties such as mesh-dependent solutions and checkerboard patterns, a density filtering technique is implemented. In these examples, topology optimization is employed to minimize structural compliance subjected to a mass budget or equivalently a volume fraction target:

\[\min_{x \in [0,1]^N}{F \cdot U(x)}\]

\[s.t.\]

\[\frac{1}{N}\sum_{i=1}^N{x_i}\leq \overline{V}\]

\[K(x)U(x) = F\]

where \(F\) is the load vector, \(U\) is the displacement vector, \(N\) is the number of elements, \(\overline{V}\) is the allowable volume fraction and \(K\) is the stiffness matrix.

[1]

Bendsøe, M. P. (1989). Optimal shape design as a material distribution problem. Structural optimization, 1(4), 193-202.

[2]

Sigmund, O. (2001). A 99 line topology optimization code written in Matlab. Structural and multidisciplinary optimization, 21(2), 120-127.

[3]

Andreassen, E., Clausen, A., Schevenels, M., Lazarov, B. S., & Sigmund, O. (2011). Efficient topology optimization in MATLAB using 88 lines of code. Structural and Multidisciplinary Optimization, 43(1), 1-16.

Solve a 2D L-shape topology optimization problem

Solve a 2D L-shape topology optimization problem

Solve a 2D MBB topology optimization problem

Solve a 2D MBB topology optimization problem

Solve a 2D short cantilever topology optimization problem

Solve a 2D short cantilever topology optimization problem