PCA on Burgers equation

Example using PCA on solutions of the Burgers equation.

from __future__ import annotations

import matplotlib.pyplot as plt
from gemseo import configure_logger
from gemseo.mlearning.transformers.dimension_reduction.pca import PCA
from gemseo.problems.dataset.burgers import create_burgers_dataset
from numpy import eye

configure_logger()

<RootLogger root (INFO)>

Load dataset

dataset = create_burgers_dataset(n_samples=20)
print(dataset)

t = dataset.input_dataset.to_numpy()[:, 0]
u_t = dataset.output_dataset.to_numpy()
t_split = 0.87

GROUP        inputs       outputs            ...
VARIABLE          t           u_t            ...
COMPONENT       0             0         1    ...       498       499           500
0          0.000000 -8.610583e-43  0.012566  ... -0.025133 -0.012566  8.610583e-43
1          0.105263 -3.809524e-01 -0.369583  ... -0.403692 -0.392322 -3.809524e-01
2          0.210526 -6.956522e-01 -0.685271  ... -0.716414 -0.706033 -6.956522e-01
3          0.315789 -9.600000e-01 -0.950450  ... -0.979101 -0.969550 -9.600000e-01
4          0.421053 -1.185185e+00 -1.176342  ... -1.202871 -1.194028 -1.185185e+00
5          0.526316 -1.379310e+00 -1.371077  ... -1.395777 -1.387543 -1.379310e+00
6          0.631579 -1.548387e+00 -1.540685  ... -1.563746 -1.556054 -1.548360e+00
7          0.736842 -1.696970e+00 -1.689735  ... -1.549187 -1.573751 -1.592272e+00
8          0.842105 -1.828571e+00 -1.821750  ...  1.522862  1.518920  1.512501e+00
9          0.947368 -1.945946e+00 -1.939493  ...  1.267586  1.274026  1.280461e+00
10         1.052632 -2.051282e+00 -2.045160  ...  0.997513  1.003635  1.009757e+00
11         1.157895 -2.146341e+00 -2.140518  ...  0.753732  0.759555  7.653786e-01
12         1.263158 -2.232558e+00 -2.227006  ...  0.532628  0.538180  5.437330e-01
13         1.368421 -2.311111e+00 -2.305805  ...  0.331178  0.336484  3.417894e-01
14         1.473684 -2.382979e+00 -2.377899  ...  0.146872  0.151952  1.570324e-01
15         1.578947 -2.448980e+00 -2.444107  ... -0.022388 -0.017515 -1.264243e-02
16         1.684211 -2.509804e+00 -2.505122  ... -0.178373 -0.173691 -1.690094e-01
17         1.789474 -2.566038e+00 -2.561533  ... -0.322585 -0.318080 -3.135751e-01
18         1.894737 -2.618182e+00 -2.613841  ... -0.456309 -0.451968 -4.476269e-01
19         2.000000 -2.666667e+00 -2.662478  ... -0.580649 -0.576460 -5.722716e-01

[20 rows x 502 columns]

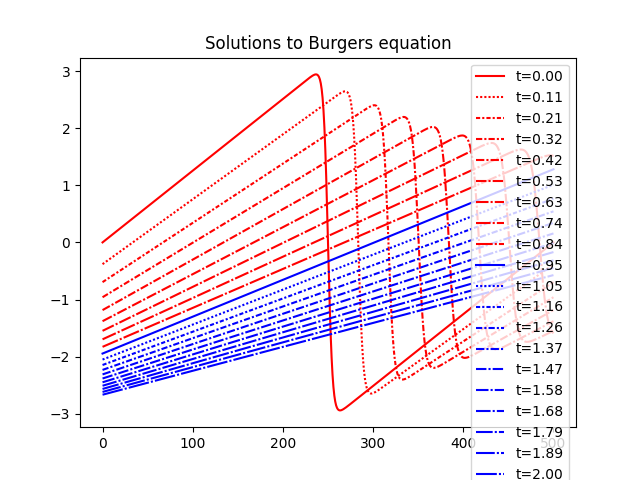
Plot dataset

def lines_gen():
    """Linestyle generator."""
    yield "-"
    for i in range(1, dataset.n_samples):
        yield 0, (i, 1, 1, 1)


color = "red"
lines = lines_gen()
for i in range(dataset.n_samples):
    # Switch mode if discontinuity is gone
    if color == "red" and t[i] > t_split:
        color = "blue"
        lines = lines_gen()  # reset linestyle generator

    plt.plot(u_t[i], color=color, linestyle=next(lines), label=f"t={t[i]:.2f}")

plt.legend()
plt.title("Solutions to Burgers equation")
plt.show()

Create PCA

n_components = 7
pca = PCA(n_components=n_components)
pca.fit(u_t)

means = u_t.mean(axis=1)
# u_t = u_t - means[:, None]

u_t_reduced = pca.transform(u_t)
u_t_restored = pca.inverse_transform(u_t_reduced)

WARNING - 16:28:27: The Scaler.fit() function does nothing; the instance of Scaler uses the coefficient and offset passed at its initialization

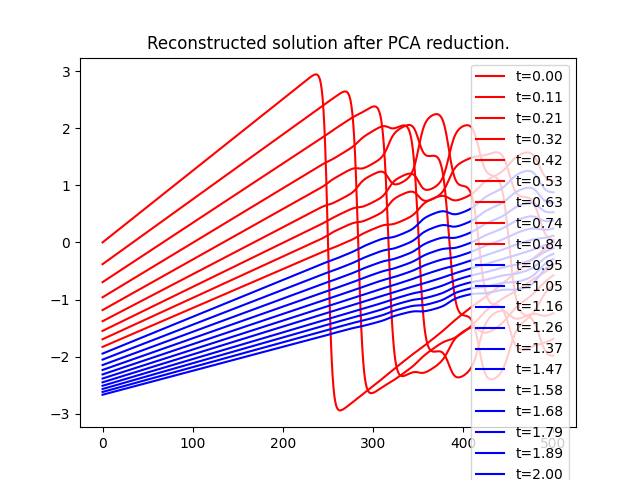
Plot restored data

color = "red"
lines = lines_gen()
for i in range(dataset.n_samples):
    # Switch mode if discontinuity is gone
    if color == "red" and t[i] > t_split:
        color = "blue"
        lines = lines_gen()  # reset linestyle generator

    plt.plot(
        u_t_restored[i],
        color=color,  # linestyle=next(lines),
        label=f"t={t[i]:.2f}",
    )
plt.legend()
plt.title("Reconstructed solution after PCA reduction.")
plt.show()

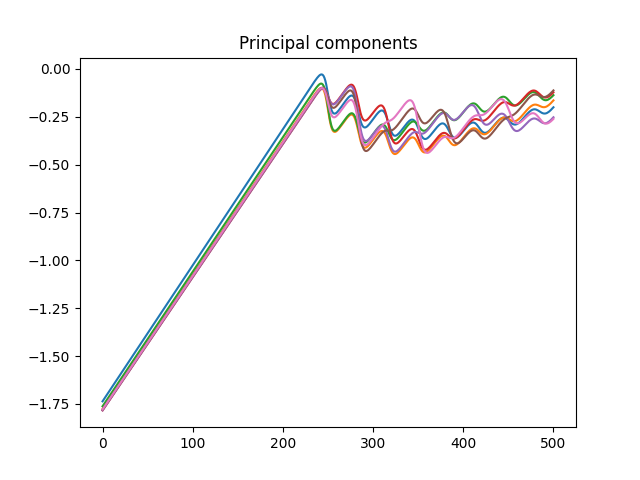
Plot principal components

red_component = eye(n_components)
components = pca.inverse_transform(red_component)
for i in range(n_components):
    plt.plot(components[i])
plt.title("Principal components")
plt.show()