Note
Go to the end to download the full example code
Application: Sobieski’s Super-Sonic Business Jet (MDO)¶
This section describes how to setup and solve the MDO problem relative to the Sobieski test case with GEMSEO.
See also
To begin with a more simple MDO problem, and have a detailed description of how to plug a test case to GEMSEO, see Tutorial: How to solve an MDO problem.
Solving with an MDF formulation¶
In this example, we solve the range optimization using the following MDF formulation:
The MDF formulation couples all the disciplines during the Multi Disciplinary Analyses at each optimization iteration.
All the design variables are equally treated, concatenated in a single vector and given to a single optimization algorithm as the unknowns of the problem.
There is no specific constraint due to the MDF formulation.
Only the design constraints \(g\_1\), \(g\_2\) and \(g\_3\) are added to the problem.
The objective function is the range (the \(y\_4\) variable in the model), computed after the Multi Disciplinary Analyses.
Imports¶
All the imports needed for the tutorials are performed here. Note that some of the imports are related to the Python 2/3 compatibility.
from __future__ import annotations
from gemseo import configure_logger
from gemseo import create_discipline
from gemseo import create_scenario
from gemseo import get_available_formulations
from gemseo.core.derivatives.jacobian_assembly import JacobianAssembly
from gemseo.disciplines.utils import get_all_inputs
from gemseo.disciplines.utils import get_all_outputs
from gemseo.problems.sobieski.core.problem import SobieskiProblem
configure_logger()
<RootLogger root (INFO)>
Step 1: Creation of MDODiscipline¶
To build the scenario, we first instantiate the disciplines. Here, the disciplines themselves have already been developed and interfaced with GEMSEO (see Benchmark problems).
disciplines = create_discipline(
[
"SobieskiPropulsion",
"SobieskiAerodynamics",
"SobieskiMission",
"SobieskiStructure",
]
)
Tip
For the disciplines that are not interfaced with GEMSEO, the GEMSEO’s
gemseo eases the creation of disciplines without having
to import them.
Step 2: Creation of Scenario¶
The scenario delegates the creation of the optimization problem to the MDO formulation.
Therefore, it needs the list of disciplines, the names of the formulation,
the name of the objective function and the design space.
The
design_space(shown below for reference, asdesign_space.txt) defines the unknowns of the optimization problem, and their bounds. It contains all the design variables needed by the MDF formulation. It can be imported from a text file, or created from scratch with the methodscreate_design_space()andadd_variable(). In this case, we will create it directly from the API.
design_space = SobieskiProblem().design_space
vi design_space.csv
name lower_bound value upper_bound type
x_shared 0.01 0.05 0.09 float
x_shared 30000.0 45000.0 60000.0 float
x_shared 1.4 1.6 1.8 float
x_shared 2.5 5.5 8.5 float
x_shared 40.0 55.0 70.0 float
x_shared 500.0 1000.0 1500.0 float
x_1 0.1 0.25 0.4 float
x_1 0.75 1.0 1.25 float
x_2 0.75 1.0 1.25 float
x_3 0.1 0.5 1.0 float
y_14 24850.0 50606.9741711 77100.0 float
y_14 -7700.0 7306.20262124 45000.0 float
y_32 0.235 0.50279625 0.795 float
y_31 2960.0 6354.32430691 10185.0 float
y_24 0.44 4.15006276 11.13 float
y_34 0.44 1.10754577 1.98 float
y_23 3365.0 12194.2671934 26400.0 float
y_21 24850.0 50606.9741711 77250.0 float
y_12 24850.0 50606.9742 77250.0 float
y_12 0.45 0.95 1.5 float
The available MDO formulations are located in the gemseo.formulations package, see Extend GEMSEO features for extending GEMSEO with other formulations.
The
formulationclassname (here,"MDF") shall be passed to the scenario to select them.The list of available formulations can be obtained by using
get_available_formulations().
get_available_formulations()
['BiLevel', 'DisciplinaryOpt', 'IDF', 'MDF']
\(y\_4\) corresponds to the
objective_name. This name must be one of the disciplines outputs, here the “SobieskiMission” discipline. The list of all outputs of the disciplines can be obtained by usingget_all_outputs():
get_all_outputs(disciplines)
get_all_inputs(disciplines)
['c_0', 'c_1', 'c_2', 'c_3', 'c_4', 'x_1', 'x_2', 'x_3', 'x_shared', 'y_12', 'y_14', 'y_21', 'y_23', 'y_24', 'y_31', 'y_32', 'y_34']
From these MDODiscipline, design space filename,
MDO formulation name and objective function name,
we build the scenario:
scenario = create_scenario(
disciplines,
formulation="MDF",
maximize_objective=True,
objective_name="y_4",
design_space=design_space,
)
The range function (\(y\_4\)) should be maximized. However, optimizers
minimize functions by default. Which is why, when creating the scenario, the argument
maximize_objective shall be set to True.
Scenario options¶
We may provide additional options to the scenario:
Function derivatives. As analytical disciplinary derivatives are vailable for Sobieski test-case, they can be used instead of computing the derivatives with finite-differences or with the complex-step method. The easiest way to set a method is to let the optimizer determine it:
scenario.set_differentiation_method()
The default behavior of the optimizer triggers finite differences. It corresponds to:
scenario.set_differentiation_method("finite_differences",1e-7)
It it also possible to differentiate functions by means of the complex step method:
scenario.set_differentiation_method("complex_step",1e-30j)
Constraints¶
Similarly to the objective function, the constraints names are a subset
of the disciplines’ outputs. They can be obtained by using
get_all_outputs().
The formulation has a powerful feature to automatically dispatch the constraints
(\(g\_1, g\_2, g\_3\)) and plug them to the optimizers depending on
the formulation. To do that, we use the method
add_constraint():
for constraint in ["g_1", "g_2", "g_3"]:
scenario.add_constraint(constraint, "ineq")
Step 3: Execution and visualization of the results¶
The algorithm arguments are provided as a dictionary to the execution method of the scenario:
algo_args = {"max_iter": 10, "algo": "SLSQP"}
Warning
The mandatory arguments are the maximum number of iterations and the algorithm name.
Any other options of the optimization algorithm can be prescribed through
the argument algo_options with a dictionary, e.g.
algo_args =
{"max_iter": 10, "algo": "SLSQP": "algo_options": {"ftol_rel": 1e-6}}.
This list of available algorithm options are detailed here: Optimization algorithms.
The scenario is executed by means of the line:
scenario.execute(algo_args)
INFO - 13:51:19:
INFO - 13:51:19: *** Start MDOScenario execution ***
INFO - 13:51:19: MDOScenario
INFO - 13:51:19: Disciplines: SobieskiAerodynamics SobieskiMission SobieskiPropulsion SobieskiStructure
INFO - 13:51:19: MDO formulation: MDF
INFO - 13:51:19: Optimization problem:
INFO - 13:51:19: minimize -y_4(x_shared, x_1, x_2, x_3)
INFO - 13:51:19: with respect to x_1, x_2, x_3, x_shared
INFO - 13:51:19: subject to constraints:
INFO - 13:51:19: g_1(x_shared, x_1, x_2, x_3) <= 0.0
INFO - 13:51:19: g_2(x_shared, x_1, x_2, x_3) <= 0.0
INFO - 13:51:19: g_3(x_shared, x_1, x_2, x_3) <= 0.0
INFO - 13:51:19: over the design space:
INFO - 13:51:19: +-------------+-------------+-------+-------------+-------+
INFO - 13:51:19: | name | lower_bound | value | upper_bound | type |
INFO - 13:51:19: +-------------+-------------+-------+-------------+-------+
INFO - 13:51:19: | x_shared[0] | 0.01 | 0.05 | 0.09 | float |
INFO - 13:51:19: | x_shared[1] | 30000 | 45000 | 60000 | float |
INFO - 13:51:19: | x_shared[2] | 1.4 | 1.6 | 1.8 | float |
INFO - 13:51:19: | x_shared[3] | 2.5 | 5.5 | 8.5 | float |
INFO - 13:51:19: | x_shared[4] | 40 | 55 | 70 | float |
INFO - 13:51:19: | x_shared[5] | 500 | 1000 | 1500 | float |
INFO - 13:51:19: | x_1[0] | 0.1 | 0.25 | 0.4 | float |
INFO - 13:51:19: | x_1[1] | 0.75 | 1 | 1.25 | float |
INFO - 13:51:19: | x_2 | 0.75 | 1 | 1.25 | float |
INFO - 13:51:19: | x_3 | 0.1 | 0.5 | 1 | float |
INFO - 13:51:19: +-------------+-------------+-------+-------------+-------+
INFO - 13:51:19: Solving optimization problem with algorithm SLSQP:
INFO - 13:51:19: ... 0%| | 0/10 [00:00<?, ?it]
INFO - 13:51:19: ... 10%|█ | 1/10 [00:00<00:01, 8.85 it/sec, obj=-536]
INFO - 13:51:19: ... 20%|██ | 2/10 [00:00<00:01, 6.58 it/sec, obj=-2.12e+3]
WARNING - 13:51:20: MDAJacobi has reached its maximum number of iterations but the normed residual 1.7130677857005655e-05 is still above the tolerance 1e-06.
INFO - 13:51:20: ... 30%|███ | 3/10 [00:00<00:01, 5.54 it/sec, obj=-3.75e+3]
INFO - 13:51:20: ... 40%|████ | 4/10 [00:00<00:01, 5.34 it/sec, obj=-3.96e+3]
INFO - 13:51:20: ... 50%|█████ | 5/10 [00:00<00:00, 5.21 it/sec, obj=-3.96e+3]
INFO - 13:51:20: Optimization result:
INFO - 13:51:20: Optimizer info:
INFO - 13:51:20: Status: 8
INFO - 13:51:20: Message: Positive directional derivative for linesearch
INFO - 13:51:20: Number of calls to the objective function by the optimizer: 6
INFO - 13:51:20: Solution:
INFO - 13:51:20: The solution is feasible.
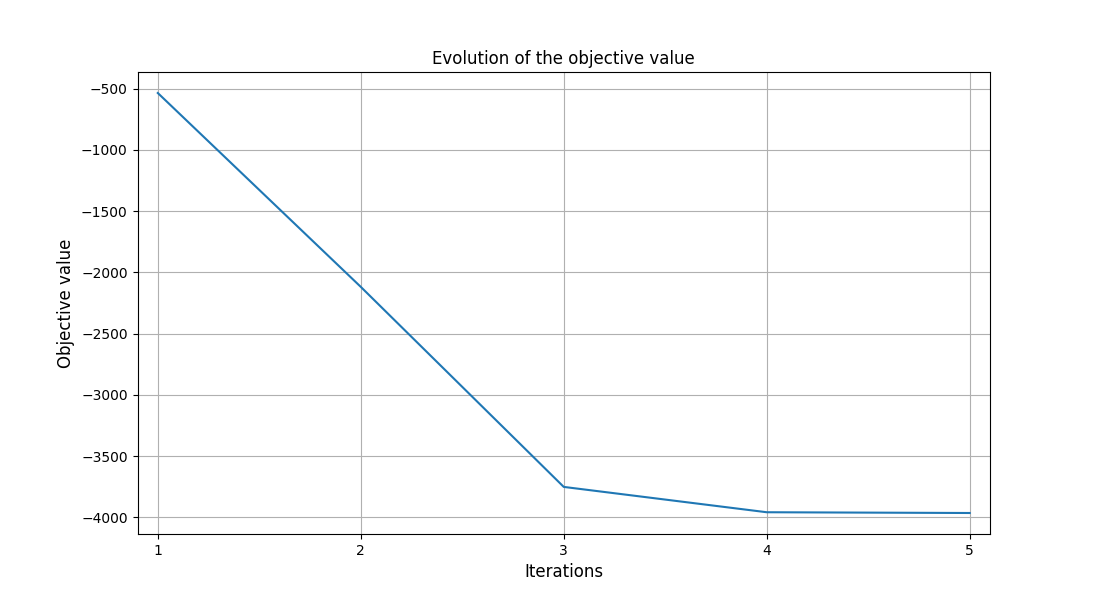
INFO - 13:51:20: Objective: -3963.408265187933
INFO - 13:51:20: Standardized constraints:
INFO - 13:51:20: g_1 = [-0.01806104 -0.03334642 -0.04424946 -0.0518346 -0.05732607 -0.13720865
INFO - 13:51:20: -0.10279135]
INFO - 13:51:20: g_2 = 3.333278582928756e-06
INFO - 13:51:20: g_3 = [-7.67181773e-01 -2.32818227e-01 8.30379541e-07 -1.83255000e-01]
INFO - 13:51:20: Design space:
INFO - 13:51:20: +-------------+-------------+---------------------+-------------+-------+
INFO - 13:51:20: | name | lower_bound | value | upper_bound | type |
INFO - 13:51:20: +-------------+-------------+---------------------+-------------+-------+
INFO - 13:51:20: | x_shared[0] | 0.01 | 0.06000083331964572 | 0.09 | float |
INFO - 13:51:20: | x_shared[1] | 30000 | 60000 | 60000 | float |
INFO - 13:51:20: | x_shared[2] | 1.4 | 1.4 | 1.8 | float |
INFO - 13:51:20: | x_shared[3] | 2.5 | 2.5 | 8.5 | float |
INFO - 13:51:20: | x_shared[4] | 40 | 70 | 70 | float |
INFO - 13:51:20: | x_shared[5] | 500 | 1500 | 1500 | float |
INFO - 13:51:20: | x_1[0] | 0.1 | 0.4 | 0.4 | float |
INFO - 13:51:20: | x_1[1] | 0.75 | 0.75 | 1.25 | float |
INFO - 13:51:20: | x_2 | 0.75 | 0.75 | 1.25 | float |
INFO - 13:51:20: | x_3 | 0.1 | 0.1562448753887276 | 1 | float |
INFO - 13:51:20: +-------------+-------------+---------------------+-------------+-------+
INFO - 13:51:20: *** End MDOScenario execution (time: 0:00:01.093001) ***
{'max_iter': 10, 'algo': 'SLSQP'}
Post-processing options¶
A whole variety of visualizations may be displayed for both MDO and DOE scenarios. These features are illustrated on the SSBJ use case in How to deal with post-processing.
To visualize the optimization history:
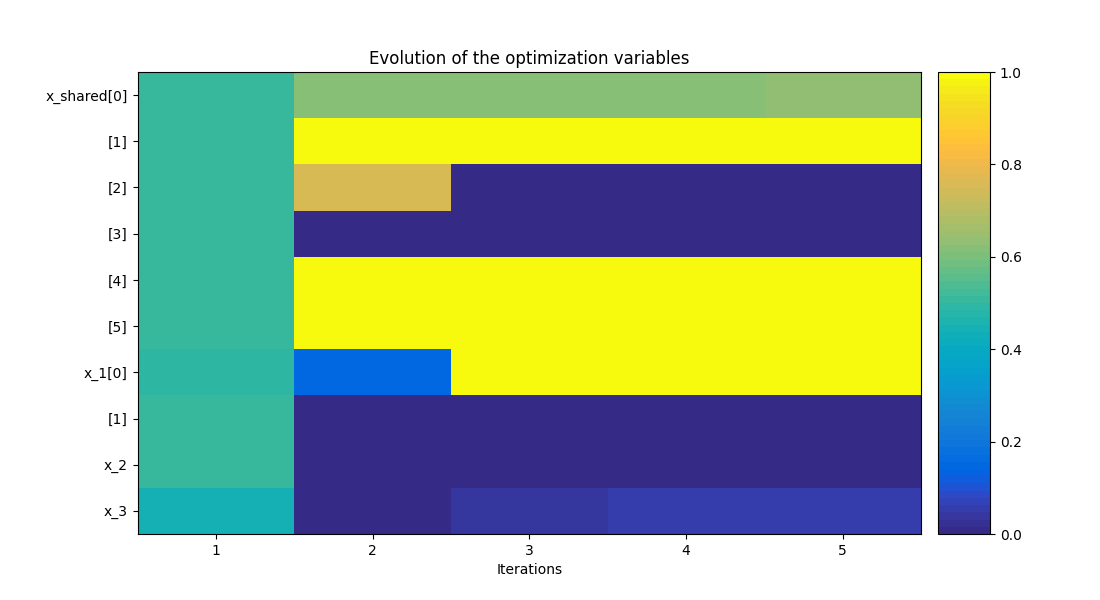
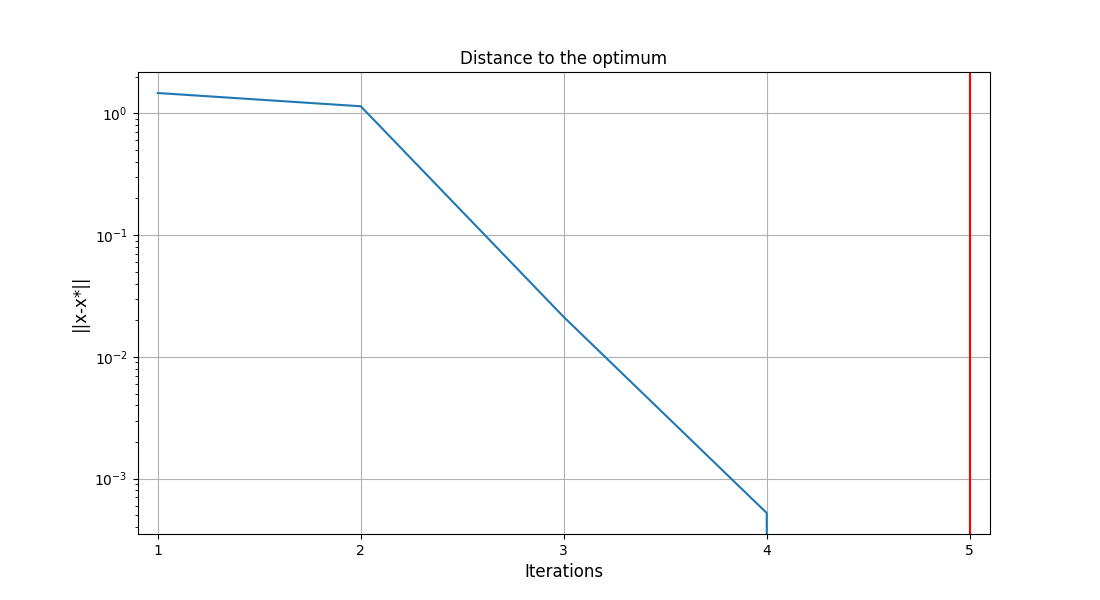
scenario.post_process("OptHistoryView", save=False, show=True)
<gemseo.post.opt_history_view.OptHistoryView object at 0x7f007b7ff880>
Influence of gradient computation method on performance¶
As mentioned in Coupled derivatives computation, several methods are available in order to perform the gradient computations: classical finite differences, complex step and Multi Disciplinary Analyses linearization in direct or adjoint mode. These modes are automatically selected by GEMSEO to minimize the CPU time. Yet, they can be forced on demand in each Multi Disciplinary Analyses:
scenario.formulation.mda.linearization_mode = JacobianAssembly.DerivationMode.DIRECT
scenario.formulation.mda.matrix_type = JacobianAssembly.JacobianType.LINEAR_OPERATOR
The method used to solve the adjoint or direct linear problem may also be selected. GEMSEO can either assemble a sparse residual Jacobian matrix of the Multi Disciplinary Analyses from the disciplines matrices. This has the advantage that LU factorizations may be stored to solve multiple right hand sides problems in a cheap way. But this requires extra memory.
scenario.formulation.mda.matrix_type = JacobianAssembly.JacobianType.MATRIX
scenario.formulation.mda.use_lu_fact = True
Altenatively, GEMSEO can implicitly create a matrix-vector product operator, which is sufficient for GMRES-like solvers. It avoids to create an additional data structure. This can also be mandatory if the disciplines do not provide full Jacobian matrices but only matrix-vector product operators.
scenario.formulation.mda.matrix_type = JacobianAssembly.JacobianType.LINEAR_OPERATOR
The next table shows the performance of each method for solving the Sobieski use case with MDF and IDF formulations. Efficiency of linearization is clearly visible has it takes from 10 to 20 times less CPU time to compute analytic derivatives of an Multi Disciplinary Analyses compared to finite difference and complex step. For IDF, improvements are less consequent, but direct linearization is more than 2.5 times faster than other methods.
Derivation Method |
Execution time (s) |
|
|---|---|---|
Finite differences |
8.22 |
1.93 |
Complex step |
18.11 |
2.07 |
Linearized (direct) |
0.90 |
0.68 |
Total running time of the script: (0 minutes 2.324 seconds)