Note
Go to the end to download the full example code
Quadratic approximations¶
In this example, we illustrate the use of the QuadApprox plot
on the Sobieski’s SSBJ problem.
from __future__ import annotations
from gemseo import configure_logger
from gemseo import create_discipline
from gemseo import create_scenario
from gemseo.problems.sobieski.core.problem import SobieskiProblem
Import¶
The first step is to import some high-level functions and a method to get the design space.
configure_logger()
<RootLogger root (INFO)>
Description¶
The QuadApprox post-processing
performs a quadratic approximation of a given function
from an optimization history
and plot the results as cuts of the approximation.
Create disciplines¶
Then, we instantiate the disciplines of the Sobieski’s SSBJ problem: Propulsion, Aerodynamics, Structure and Mission
disciplines = create_discipline(
[
"SobieskiPropulsion",
"SobieskiAerodynamics",
"SobieskiStructure",
"SobieskiMission",
]
)
Create design space¶
We also read the design space from the SobieskiProblem.
design_space = SobieskiProblem().design_space
Create and execute scenario¶
The next step is to build an MDO scenario in order to maximize the range, encoded ‘y_4’, with respect to the design parameters, while satisfying the inequality constraints ‘g_1’, ‘g_2’ and ‘g_3’. We can use the MDF formulation, the SLSQP optimization algorithm and a maximum number of iterations equal to 100.
scenario = create_scenario(
disciplines,
formulation="MDF",
objective_name="y_4",
maximize_objective=True,
design_space=design_space,
)
scenario.set_differentiation_method()
for constraint in ["g_1", "g_2", "g_3"]:
scenario.add_constraint(constraint, "ineq")
scenario.execute({"algo": "SLSQP", "max_iter": 10})
INFO - 13:56:20:
INFO - 13:56:20: *** Start MDOScenario execution ***
INFO - 13:56:20: MDOScenario
INFO - 13:56:20: Disciplines: SobieskiAerodynamics SobieskiMission SobieskiPropulsion SobieskiStructure
INFO - 13:56:20: MDO formulation: MDF
INFO - 13:56:20: Optimization problem:
INFO - 13:56:20: minimize -y_4(x_shared, x_1, x_2, x_3)
INFO - 13:56:20: with respect to x_1, x_2, x_3, x_shared
INFO - 13:56:20: subject to constraints:
INFO - 13:56:20: g_1(x_shared, x_1, x_2, x_3) <= 0.0
INFO - 13:56:20: g_2(x_shared, x_1, x_2, x_3) <= 0.0
INFO - 13:56:20: g_3(x_shared, x_1, x_2, x_3) <= 0.0
INFO - 13:56:20: over the design space:
INFO - 13:56:20: +-------------+-------------+-------+-------------+-------+
INFO - 13:56:20: | name | lower_bound | value | upper_bound | type |
INFO - 13:56:20: +-------------+-------------+-------+-------------+-------+
INFO - 13:56:20: | x_shared[0] | 0.01 | 0.05 | 0.09 | float |
INFO - 13:56:20: | x_shared[1] | 30000 | 45000 | 60000 | float |
INFO - 13:56:20: | x_shared[2] | 1.4 | 1.6 | 1.8 | float |
INFO - 13:56:20: | x_shared[3] | 2.5 | 5.5 | 8.5 | float |
INFO - 13:56:20: | x_shared[4] | 40 | 55 | 70 | float |
INFO - 13:56:20: | x_shared[5] | 500 | 1000 | 1500 | float |
INFO - 13:56:20: | x_1[0] | 0.1 | 0.25 | 0.4 | float |
INFO - 13:56:20: | x_1[1] | 0.75 | 1 | 1.25 | float |
INFO - 13:56:20: | x_2 | 0.75 | 1 | 1.25 | float |
INFO - 13:56:20: | x_3 | 0.1 | 0.5 | 1 | float |
INFO - 13:56:20: +-------------+-------------+-------+-------------+-------+
INFO - 13:56:20: Solving optimization problem with algorithm SLSQP:
INFO - 13:56:20: ... 0%| | 0/10 [00:00<?, ?it]
INFO - 13:56:20: ... 10%|█ | 1/10 [00:00<00:01, 8.78 it/sec, obj=-536]
INFO - 13:56:20: ... 20%|██ | 2/10 [00:00<00:01, 6.48 it/sec, obj=-2.12e+3]
WARNING - 13:56:20: MDAJacobi has reached its maximum number of iterations but the normed residual 1.7130677857005655e-05 is still above the tolerance 1e-06.
INFO - 13:56:20: ... 30%|███ | 3/10 [00:00<00:01, 5.46 it/sec, obj=-3.75e+3]
INFO - 13:56:20: ... 40%|████ | 4/10 [00:00<00:01, 5.26 it/sec, obj=-3.96e+3]
INFO - 13:56:21: ... 50%|█████ | 5/10 [00:00<00:00, 5.14 it/sec, obj=-3.96e+3]
INFO - 13:56:21: Optimization result:
INFO - 13:56:21: Optimizer info:
INFO - 13:56:21: Status: 8
INFO - 13:56:21: Message: Positive directional derivative for linesearch
INFO - 13:56:21: Number of calls to the objective function by the optimizer: 6
INFO - 13:56:21: Solution:
INFO - 13:56:21: The solution is feasible.
INFO - 13:56:21: Objective: -3963.408265187933
INFO - 13:56:21: Standardized constraints:
INFO - 13:56:21: g_1 = [-0.01806104 -0.03334642 -0.04424946 -0.0518346 -0.05732607 -0.13720865
INFO - 13:56:21: -0.10279135]
INFO - 13:56:21: g_2 = 3.333278582928756e-06
INFO - 13:56:21: g_3 = [-7.67181773e-01 -2.32818227e-01 8.30379541e-07 -1.83255000e-01]
INFO - 13:56:21: Design space:
INFO - 13:56:21: +-------------+-------------+---------------------+-------------+-------+
INFO - 13:56:21: | name | lower_bound | value | upper_bound | type |
INFO - 13:56:21: +-------------+-------------+---------------------+-------------+-------+
INFO - 13:56:21: | x_shared[0] | 0.01 | 0.06000083331964572 | 0.09 | float |
INFO - 13:56:21: | x_shared[1] | 30000 | 60000 | 60000 | float |
INFO - 13:56:21: | x_shared[2] | 1.4 | 1.4 | 1.8 | float |
INFO - 13:56:21: | x_shared[3] | 2.5 | 2.5 | 8.5 | float |
INFO - 13:56:21: | x_shared[4] | 40 | 70 | 70 | float |
INFO - 13:56:21: | x_shared[5] | 500 | 1500 | 1500 | float |
INFO - 13:56:21: | x_1[0] | 0.1 | 0.4 | 0.4 | float |
INFO - 13:56:21: | x_1[1] | 0.75 | 0.75 | 1.25 | float |
INFO - 13:56:21: | x_2 | 0.75 | 0.75 | 1.25 | float |
INFO - 13:56:21: | x_3 | 0.1 | 0.1562448753887276 | 1 | float |
INFO - 13:56:21: +-------------+-------------+---------------------+-------------+-------+
INFO - 13:56:21: *** End MDOScenario execution (time: 0:00:01.109474) ***
{'max_iter': 10, 'algo': 'SLSQP'}
Post-process scenario¶
Lastly, we post-process the scenario by means of the QuadApprox
plot which performs a quadratic approximation of a given function
from an optimization history and plot the results as cuts of the
approximation.
Tip
Each post-processing method requires different inputs and offers a variety
of customization options. Use the high-level function
get_post_processing_options_schema() to print a table with
the options for any post-processing algorithm.
Or refer to our dedicated page:
Post-processing algorithms.
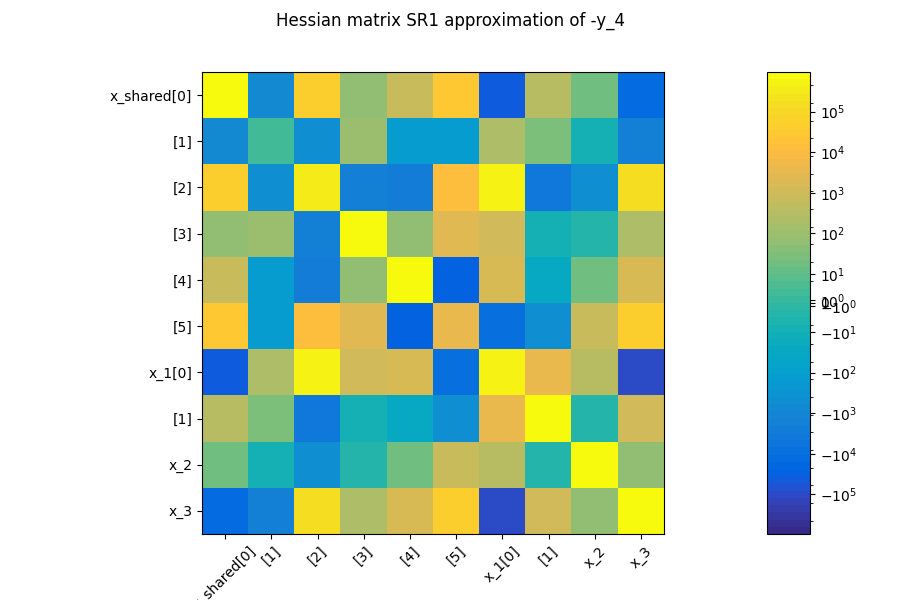
The first plot shows an approximation of the Hessian matrix \(\frac{\partial^2 f}{\partial x_i \partial x_j}\) based on the Symmetric Rank 1 method (SR1) [NW06]. The color map uses a symmetric logarithmic (symlog) scale. This plots the cross influence of the design variables on the objective function or constraints. For instance, on the last figure, the maximal second-order sensitivity is \(\frac{\partial^2 -y_4}{\partial^2 x_0} = 2.10^5\), which means that the \(x_0\) is the most influential variable. Then, the cross derivative \(\frac{\partial^2 -y_4}{\partial x_0 \partial x_2} = 5.10^4\) is positive and relatively high compared to the previous one but the combined effects of \(x_0\) and \(x_2\) are non-negligible in comparison.
scenario.post_process("QuadApprox", function="-y_4", save=False, show=True)
<gemseo.post.quad_approx.QuadApprox object at 0x7f006b656610>
The second plot represents the quadratic approximation of the objective around the optimal solution : \(a_{i}(t)=0.5 (t-x^*_i)^2 \frac{\partial^2 f}{\partial x_i^2} + (t-x^*_i) \frac{\partial f}{\partial x_i} + f(x^*)\), where \(x^*\) is the optimal solution. This approximation highlights the sensitivity of the objective function with respect to the design variables: we notice that the design variables \(x\_1, x\_5, x\_6\) have little influence , whereas \(x\_0, x\_2, x\_9\) have a huge influence on the objective. This trend is also noted in the diagonal terms of the Hessian matrix \(\frac{\partial^2 f}{\partial x_i^2}\).
Total running time of the script: (0 minutes 2.077 seconds)