Note
Go to the end to download the full example code
Scalable study¶
We want to compare IDF and MDF formulations
with respect to the problem dimension for the aerostructure problem.
For that,
we use the ScalabilityStudy and PostScalabilityStudy classes.
from __future__ import annotations
from gemseo import configure_logger
from gemseo import create_discipline
from gemseo import create_scenario
from gemseo.problems.aerostructure.aerostructure_design_space import (
AerostructureDesignSpace,
)
from gemseo.problems.scalable.data_driven import create_scalability_study
from gemseo.problems.scalable.data_driven import plot_scalability_results
configure_logger()
Create the disciplinary datasets¶
First of all, we create the disciplinary Dataset datasets
based on a DiagonalDOE.
datasets = {}
disciplines = create_discipline(["Aerodynamics", "Structure", "Mission"])
for discipline in disciplines:
design_space = AerostructureDesignSpace()
design_space.filter(discipline.get_input_data_names())
output_names = iter(discipline.get_output_data_names())
scenario = create_scenario(
discipline,
"DisciplinaryOpt",
next(output_names),
design_space,
scenario_type="DOE",
)
for output_name in output_names:
scenario.add_observable(output_name)
scenario.execute({"algo": "DiagonalDOE", "n_samples": 10})
datasets[discipline.name] = scenario.to_dataset(
name=discipline.name, opt_naming=False
)
Define the design problem¶
Then, we instantiate a ScalabilityStudy
from the definition of the design problem, expressed in terms of
objective function (to maximize or minimize),
design variables (local and global)
and constraints (equality and inequality).
We can also specify the coupling variables that we could scale.
Note that this information is only required by the scaling stage.
Indeed, MDO formulations know perfectly
how to automatically recognize the coupling variables.
Lastly, we can specify some properties of the scalable methodology
such as the fill factor
describing the level of dependence between inputs and outputs.
study = create_scalability_study(
objective="range",
design_variables=["thick_airfoils", "thick_panels", "sweep"],
eq_constraints=["c_rf"],
ineq_constraints=["c_lift"],
maximize_objective=True,
coupling_variables=["forces", "displ"],
fill_factor=-1,
)
Add the disciplinary datasets¶
study.add_discipline(datasets["Aerodynamics"])
study.add_discipline(datasets["Structure"])
study.add_discipline(datasets["Mission"])
Add the optimization strategies¶
Then, we define the different optimization strategies we want to compare: In this case, the strategies are:
MDFformulation with the"NLOPT_SLSQP"optimization algorithm and no more than 100 iterations,IDFformulation with the"NLOPT_SLSQP"optimization algorithm and no more than 100 iterations,
Note that in this case, we compare MDO formulations but we could easily compare optimization algorithms.
study.add_optimization_strategy("NLOPT_SLSQP", 100, "MDF")
study.add_optimization_strategy("NLOPT_SLSQP", 100, "IDF")
Add the scaling strategy¶
After that, we define the different scaling strategies for which we want to compare the optimization strategies. In this case, the strategies are:
All design parameters have a size equal to 1,
All design parameters have a size equal to 20.
To do that, we pass design_size=[1, 20]
to the ScalabilityStudy.add_scaling_strategies() method.
design_size expects either:
a list of integer where the ith component is the size for the ith scaling strategy,
an integer changing the fixed size (if
None, use the original size).
Note that we could also compare the optimization strategies while
varying the size of the different coupling variables (use
coupling_size),varying the size of the different equality constraints (use
eq_size),varying the size of the different inequality constraints (use
ineq_size),varying the size of any variable (use
variables),
where the corresponding arguments works in the same way as design_size,
except for variables which expects a list of dictionary
whose keys are variables names and values are variables sizes.
In this way, we can use this argument to fine-tune a scaling strategy
to very specific variables, e.g. local variables.
study.add_scaling_strategies(design_size=[1, 20])
Execute the scalable study¶
Then, we execute the scalability study,
i.e. to build and execute a ScalableProblem
for each optimization strategy and each scaling strategy,
and repeat it 2 times in order to get statistics on the results
(because the ScalableDiagonalModel relies on stochastic features.
study.execute(n_replicates=2)
Look at the dependency matrices¶
Here are the dependency matrices obtained with the 1st replicate when
design_size=10.
Aerodynamics¶
Structure¶
Mission¶
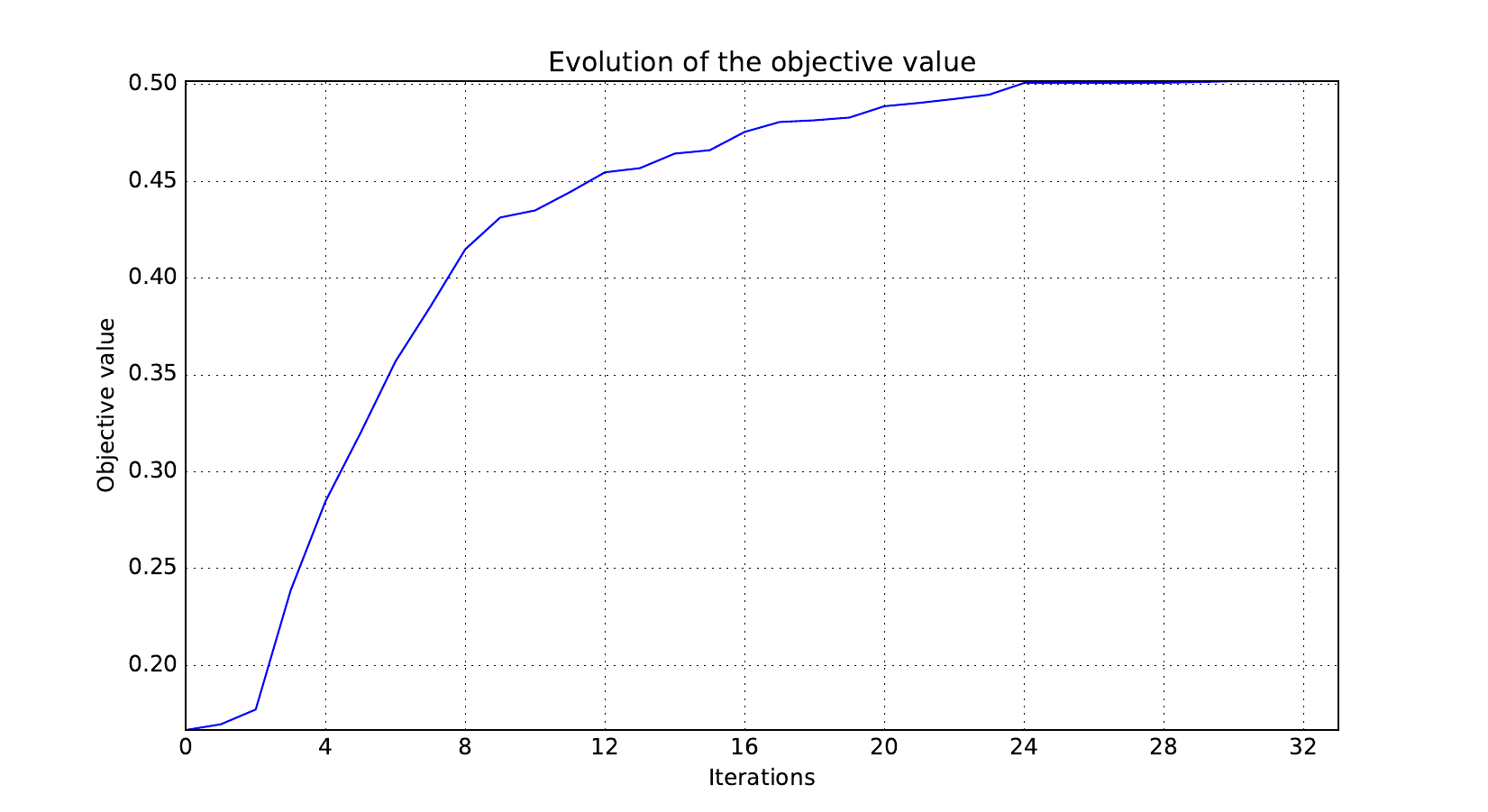
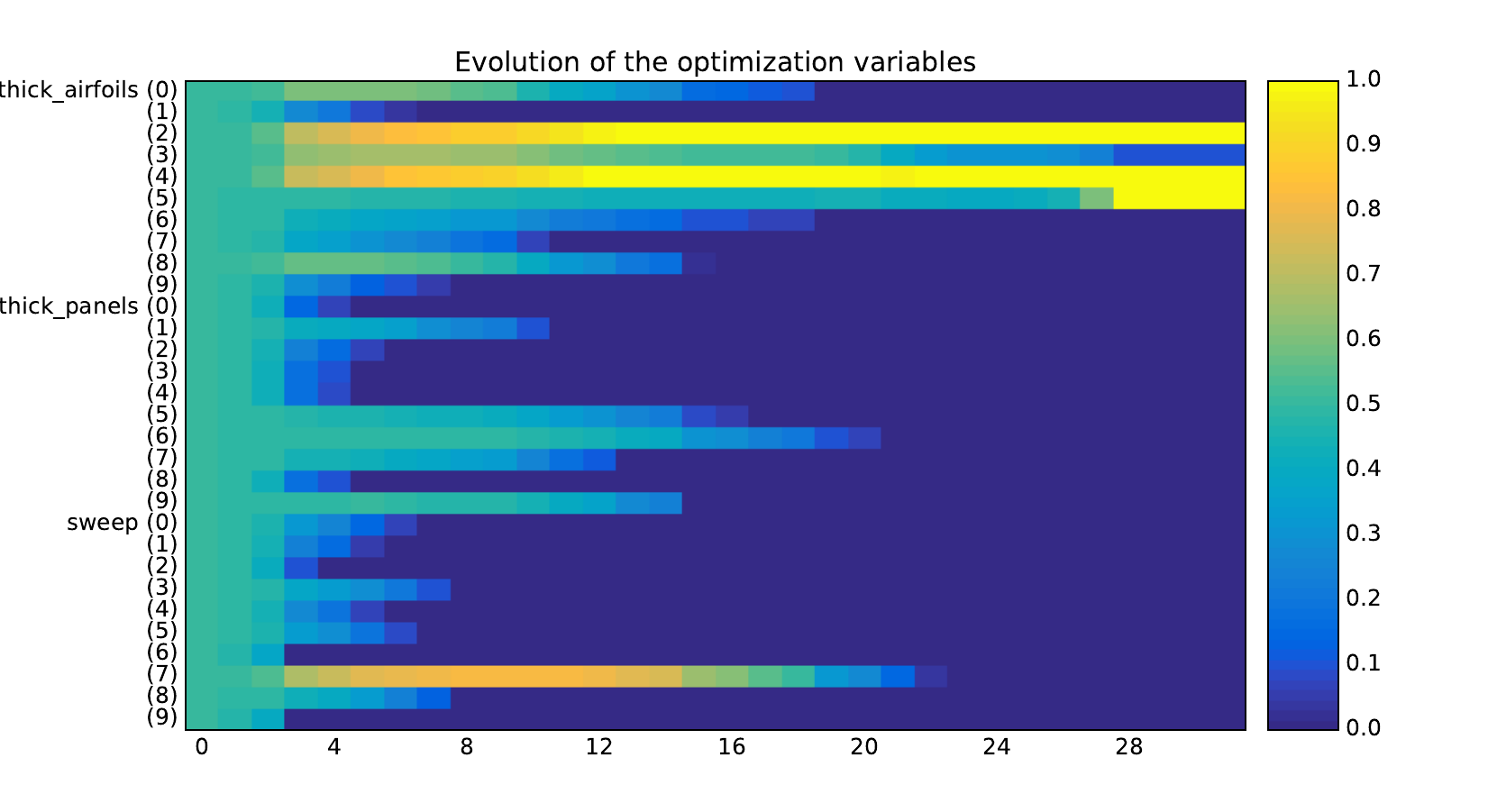
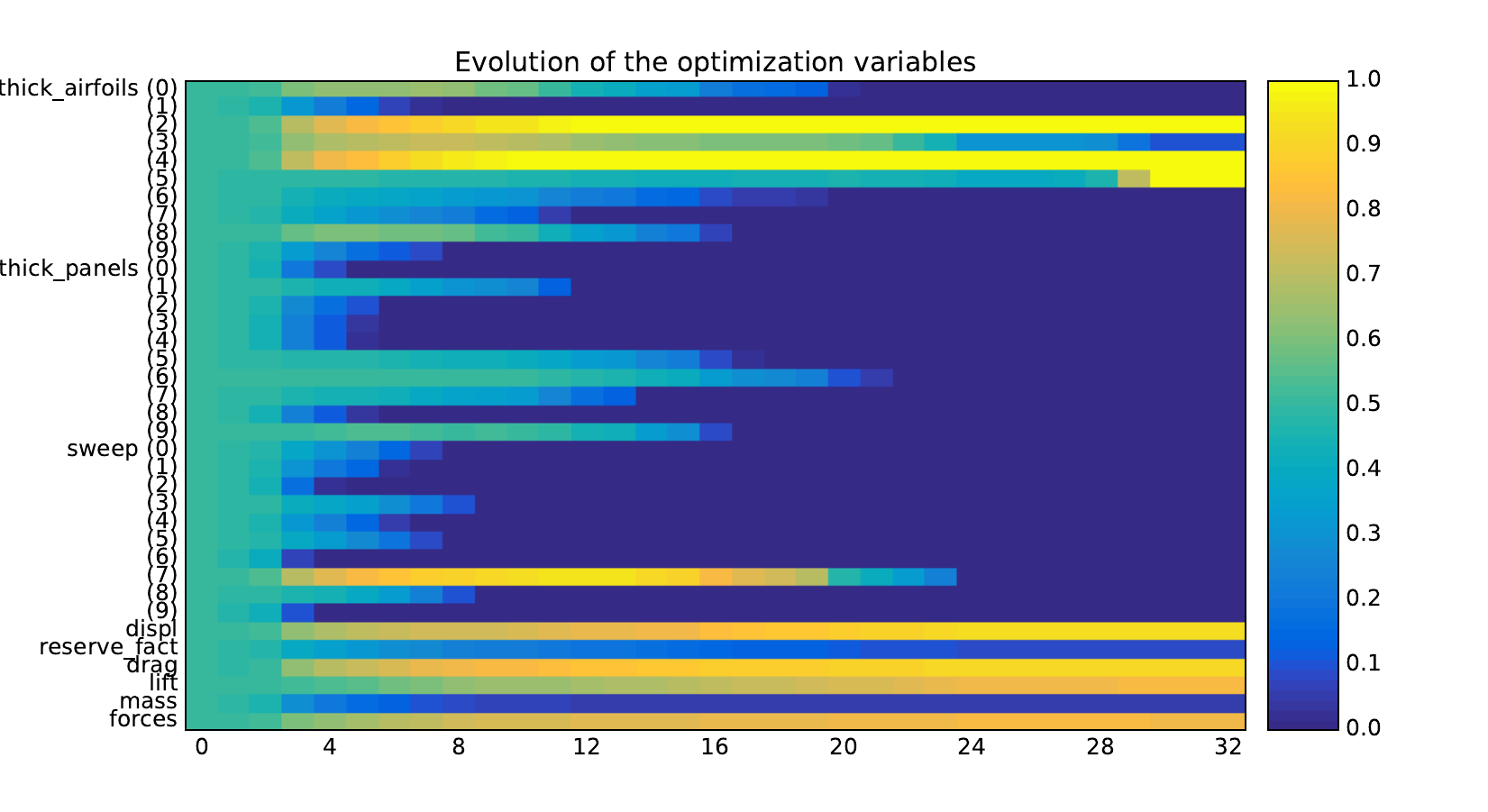
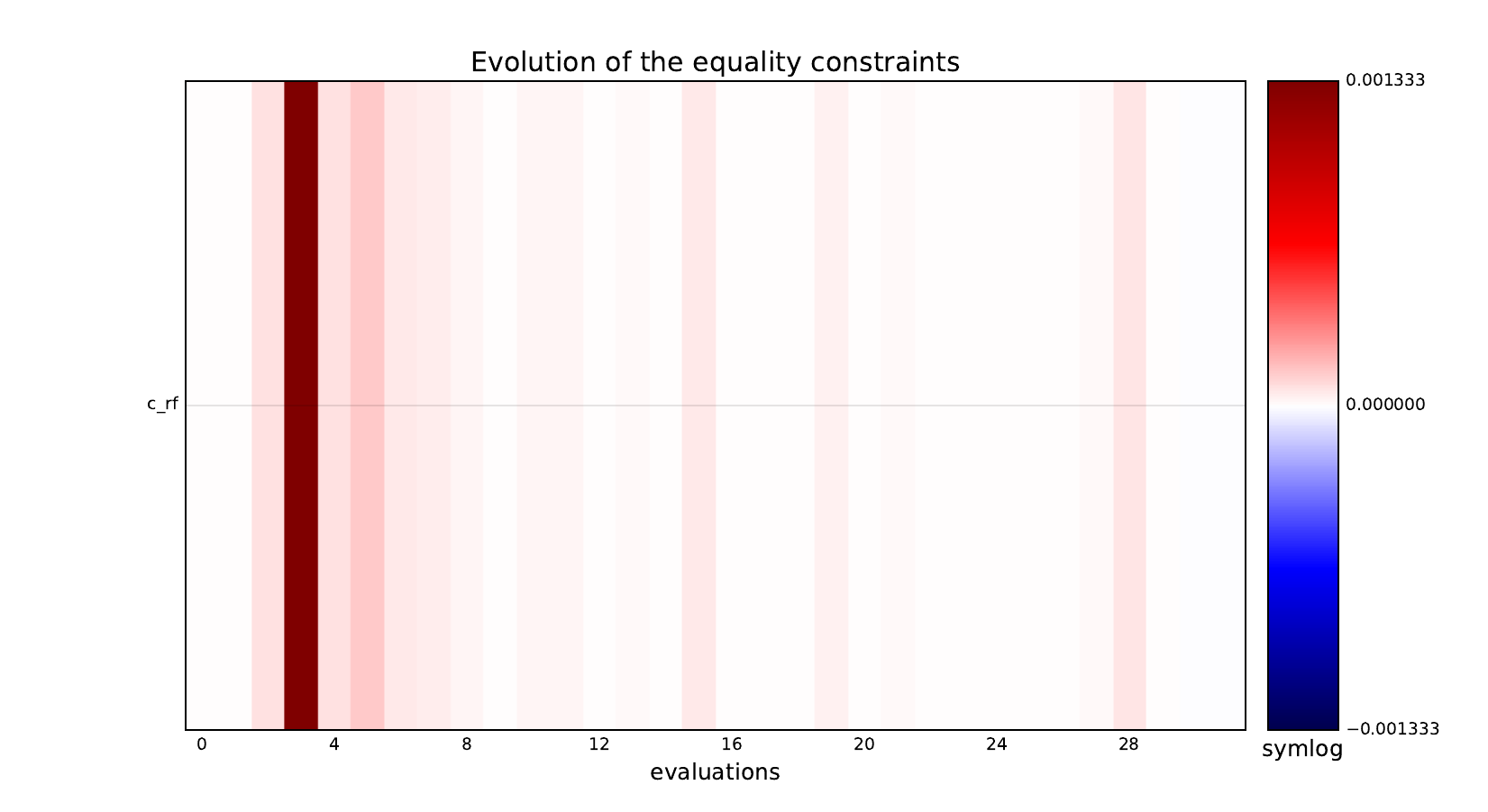
Look at optimization histories¶
Here are the optimization histories obtained with the 1st replicate when
design_size=10, where the left side represents the MDF formulation
while the right one represents the IDF formulation.
Objective function¶
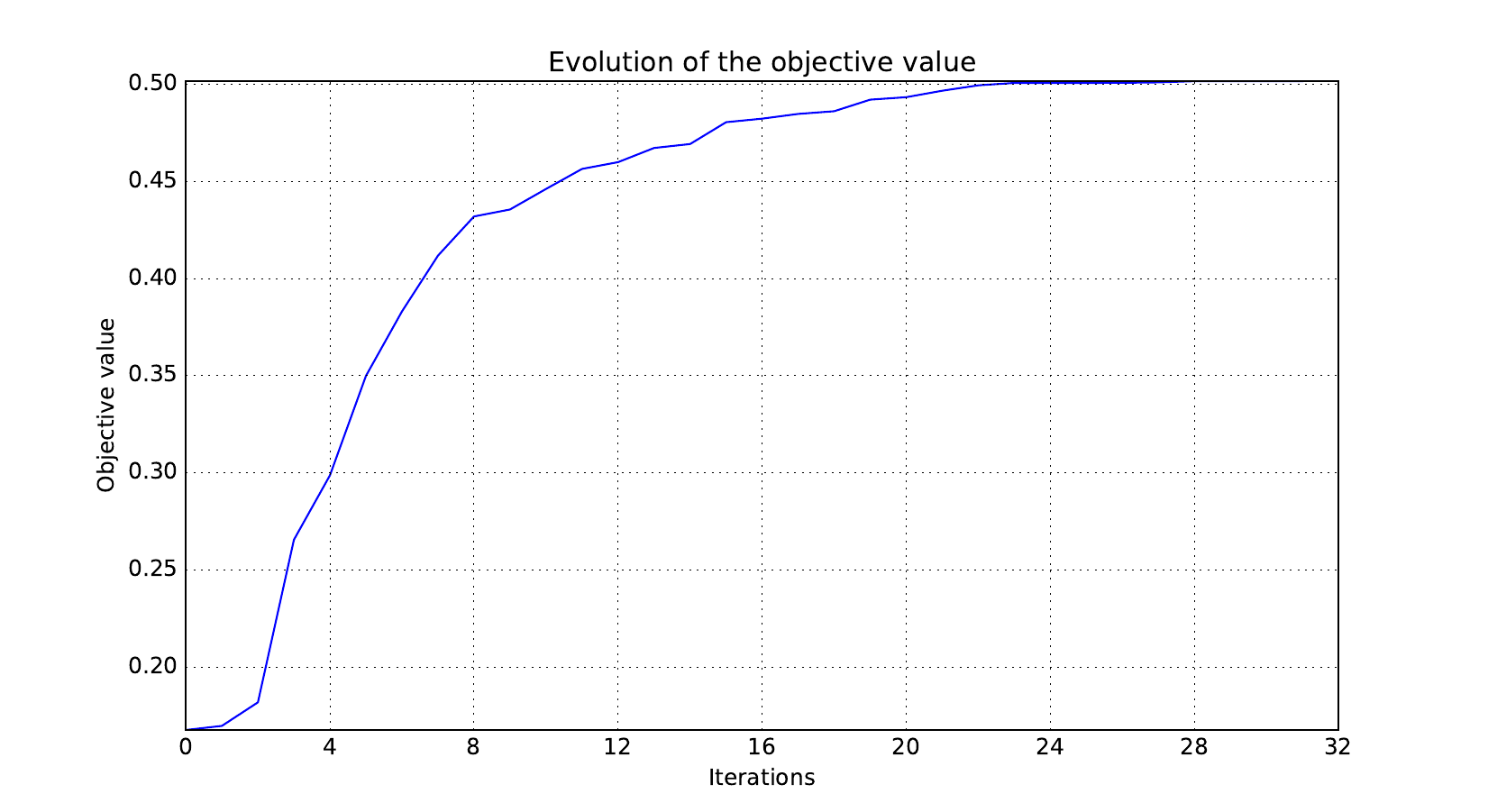
Design variables¶
Equality constraints¶
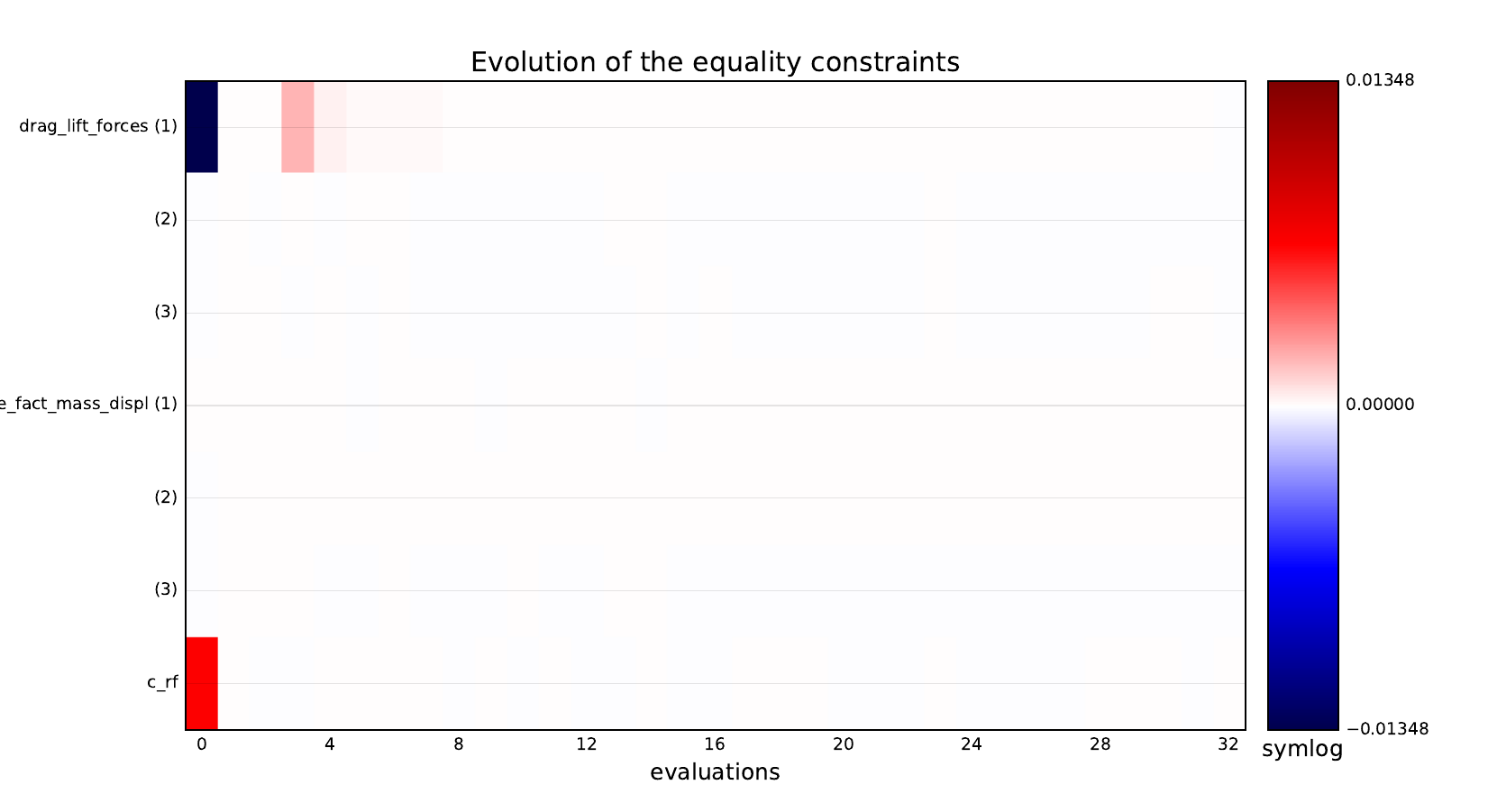
Inequality constraints¶
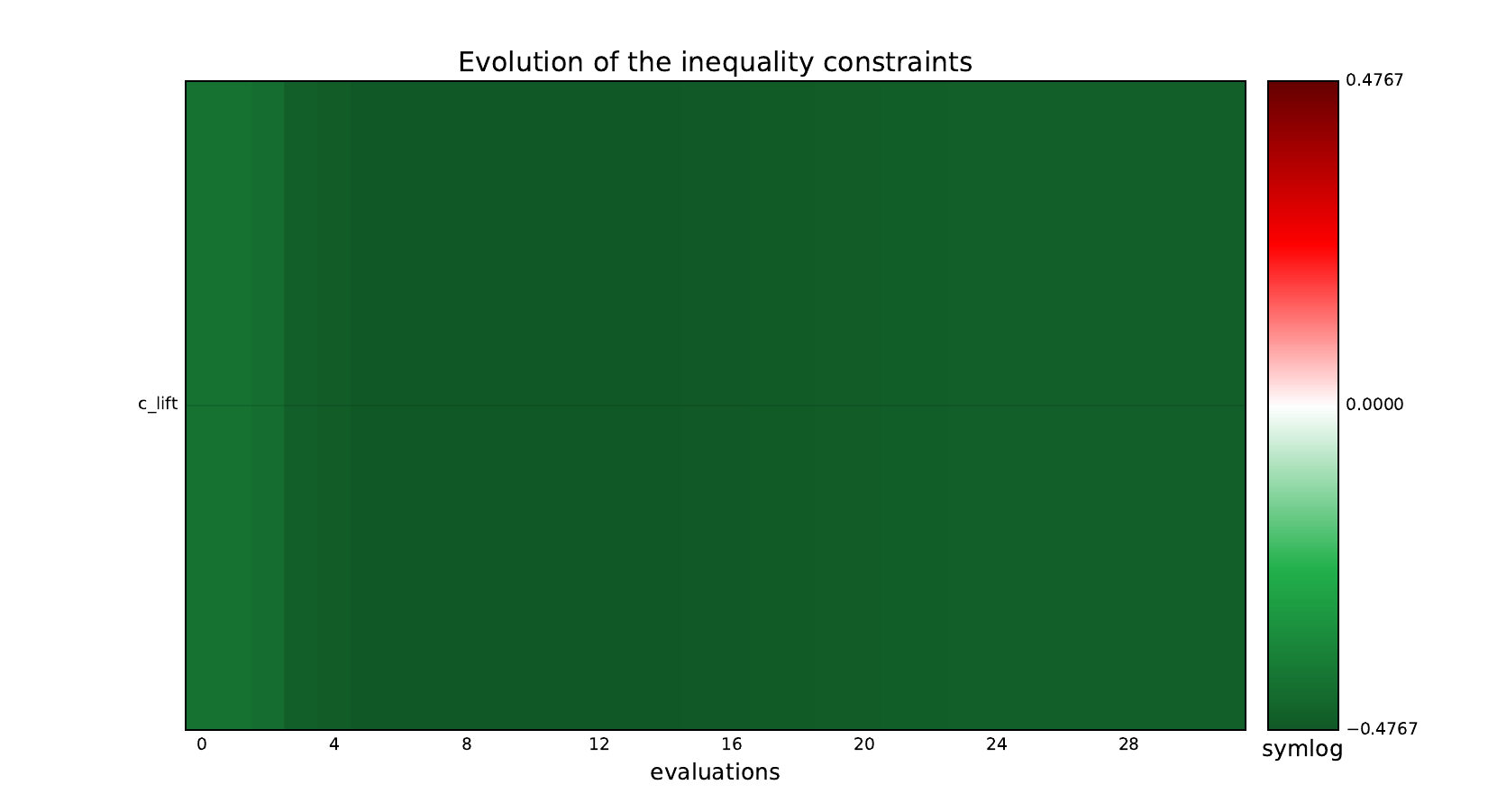
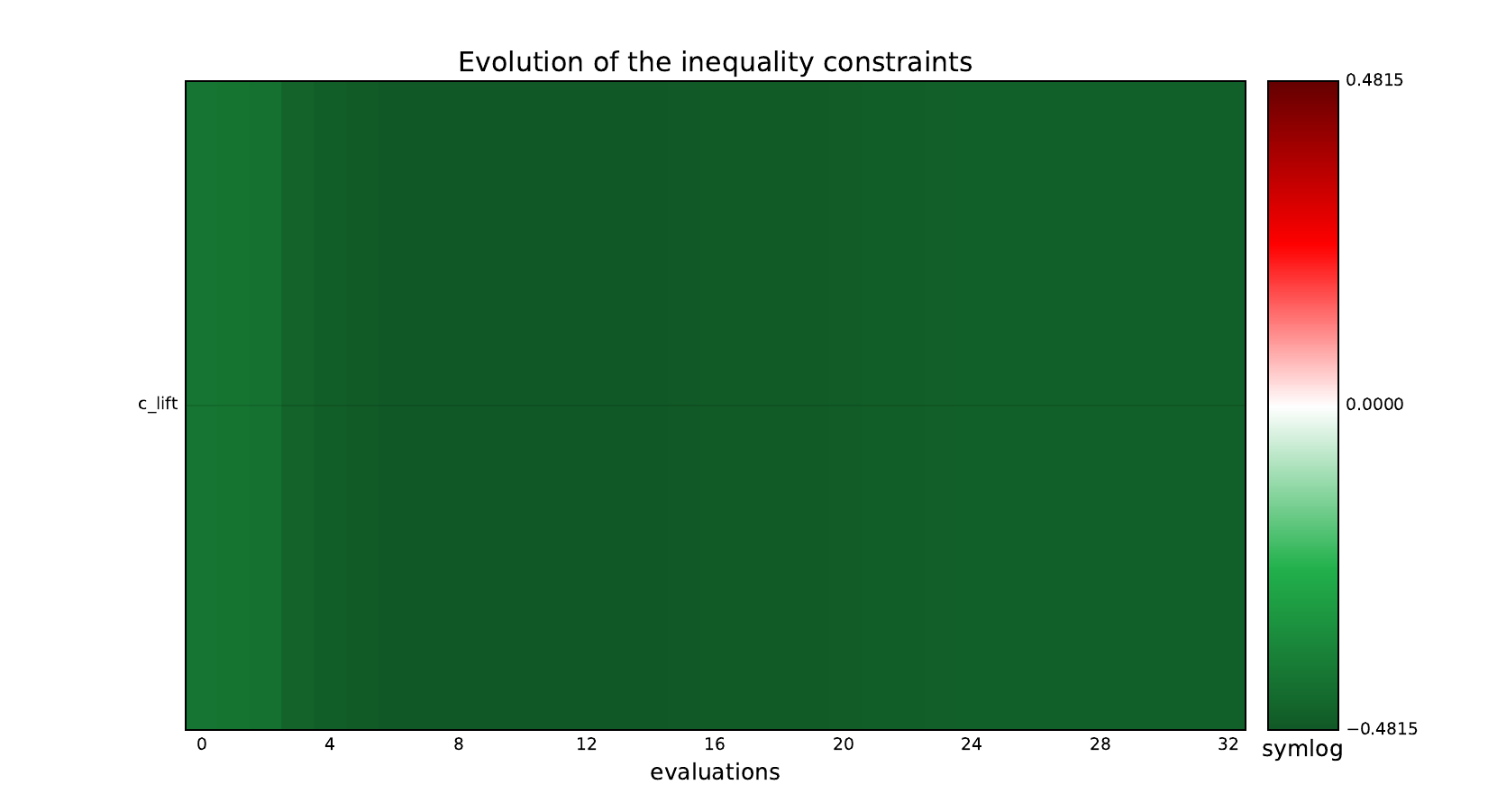
Post-process the results¶
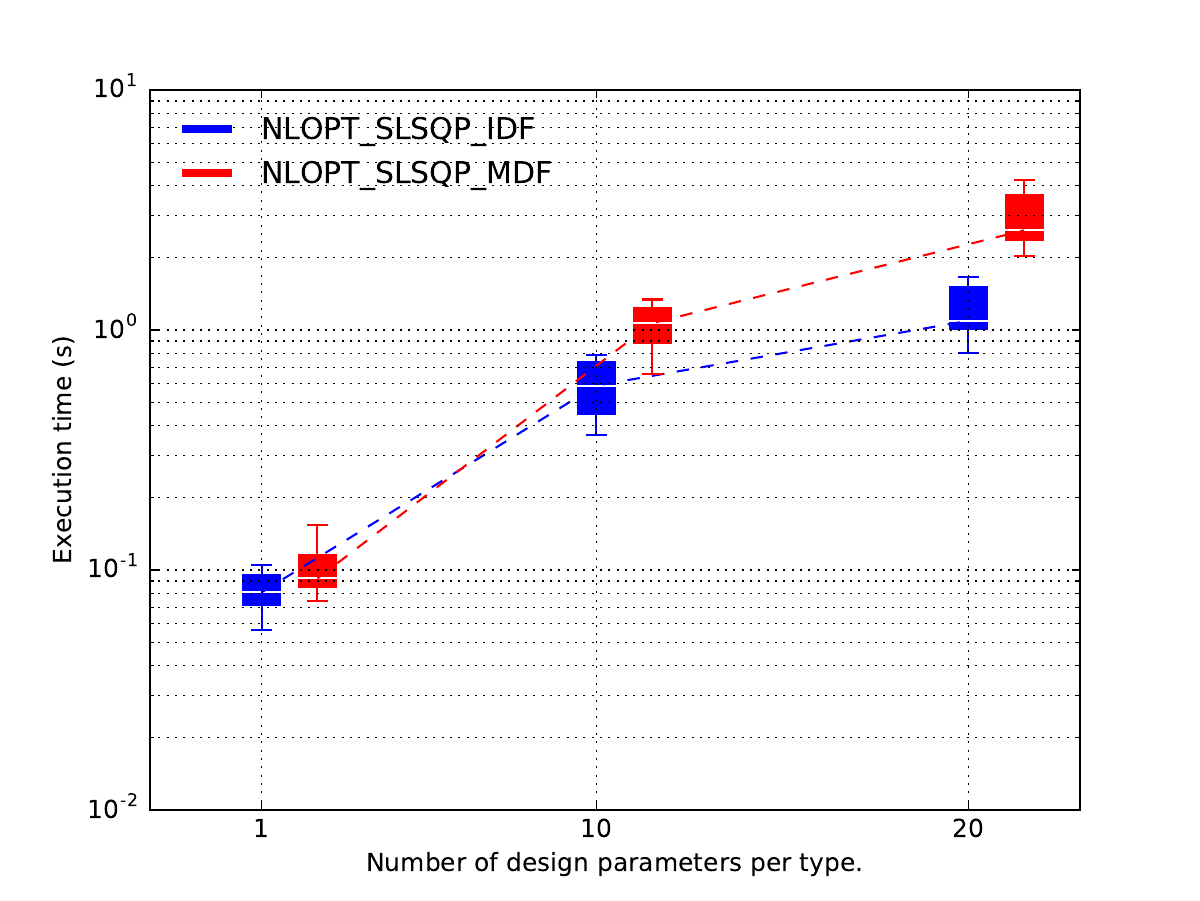
Lastly, we plot the results.
Because of the replicates,
the latter are not displayed as one line per optimization strategy
w.r.t. scaling strategy,
but as one series of boxplots per optimization strategy w.r.t. scaling strategy,
where the boxplots represents the variability due to the 10 replicates.
In this case, it seems that
the MDF formulation is more expensive than the IDF one
when the design space dimension increases
while they seems to be the same when each design parameter has a size equal to 1.
post = plot_scalability_results("study")
post.labelize_scaling_strategy("Number of design parameters per type.")
post.plot(xmargin=3.0, xticks=[1.0, 20.0], xticks_labels=["1", "20"], widths=1.0)
Total running time of the script: (0 minutes 0.000 seconds)
