parametric module¶
Class for the parametric estimation of statistics from a dataset.
Overview¶
The ParametricStatistics class inherits
from the abstract Statistics class
and aims to estimate statistics from a Dataset,
based on candidate parametric distributions calibrated from this Dataset.
For each variable,
the parameters of these distributions are calibrated from the
Dataset,the fitted parametric
Distributionwhich is optimal in the sense of a goodness-of-fit criterion and a selection criterion is selected to estimate the statistics related to this variable.
The ParametricStatistics relies on the OpenTURNS library
through the OTDistribution and OTDistributionFitter classes.
Construction¶
The ParametricStatistics is built from two mandatory arguments:
a dataset,
a list of distributions names,
and can consider optional arguments:
a subset of variables names (by default, statistics are computed for all variables),
a fitting criterion name (by default, BIC is used; see
FittingCriterionandSignificanceTestfor more information),a level associated with the fitting criterion,
a selection criterion:
‘best’: select the distribution minimizing (or maximizing, depending on the criterion) the criterion,
‘first’: select the first distribution for which the criterion is greater (or lower, depending on the criterion) than the level,
a name for the
ParametricStatisticsobject (by default, the name is the concatenation of ‘ParametricStatistics’ and the name of theDataset).
Capabilities¶
By inheritance,
a ParametricStatistics object has
the same capabilities as Statistics.
Additional ones are:
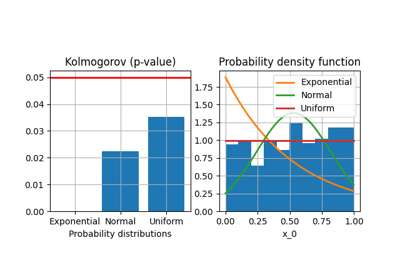
get_fitting_matrix(): this method displays the values of the fitting criterion for the different variables and candidate probability distributions as well as the select probability distribution,plot_criteria(): this method plots the criterion values for a given variable.
- class gemseo.uncertainty.statistics.parametric.ParametricStatistics(dataset, distributions, variable_names=(), fitting_criterion=FittingCriterion.BIC, level=0.05, selection_criterion=SelectionCriterion.BEST, name='')[source]
Bases:
StatisticsA toolbox to compute statistics based on probability distribution-fitting.
Unless otherwise stated, the statistics are computed variable-wise and component-wise, i.e. variable-by-variable and component-by-component. So, for the sake of readability, the methods named as
compute_statistic()returndict[str, ndarray]objects whose values are the names of the variables and the values are the statistic estimated for the different component.Examples
>>> from gemseo import ( ... create_discipline, ... create_parameter_space, ... create_scenario, ... ) >>> from gemseo.uncertainty.statistics.parametric import ParametricStatistics >>> >>> expressions = {"y1": "x1+2*x2", "y2": "x1-3*x2"} >>> discipline = create_discipline( ... "AnalyticDiscipline", expressions=expressions ... ) >>> >>> parameter_space = create_parameter_space() >>> parameter_space.add_random_variable( ... "x1", "OTUniformDistribution", minimum=-1, maximum=1 ... ) >>> parameter_space.add_random_variable( ... "x2", "OTNormalDistribution", mu=0.5, sigma=2 ... ) >>> >>> scenario = create_scenario( ... [discipline], ... "DisciplinaryOpt", ... "y1", ... parameter_space, ... scenario_type="DOE", ... ) >>> scenario.execute({"algo": "OT_MONTE_CARLO", "n_samples": 100}) >>> >>> dataset = scenario.to_dataset(opt_naming=False) >>> >>> statistics = ParametricStatistics( ... dataset, ["Normal", "Uniform", "Triangular"] ... ) >>> fitting_matrix = statistics.get_fitting_matrix() >>> mean = statistics.compute_mean()
- Parameters:
dataset (Dataset) – A dataset.
distributions (Sequence[DistributionName]) – The names of the distributions.
variable_names (Iterable[str]) –
The names of the variables for which to compute statistics. If empty, consider all the variables of the dataset.
By default it is set to ().
fitting_criterion (FittingCriterion) –
The name of the goodness-of-fit criterion, measuring how the distribution fits the data. Use
ParametricStatistics.get_criteria()to get the available criteria.By default it is set to “BIC”.
level (float) –
A test level, i.e. the risk of committing a Type 1 error, that is an incorrect rejection of a true null hypothesis, for criteria based on test hypothesis.
By default it is set to 0.05.
selection_criterion (SelectionCriterion) –
The selection criterion to select a distribution from a list of candidates.
By default it is set to “best”.
name (str) –
A name for the toolbox computing statistics. If empty, concatenate the names of the dataset and the name of the class.
By default it is set to “”.
- class DistributionName(value)
Bases:
StrEnumAn enumeration.
- Arcsine = 'Arcsine'
- Beta = 'Beta'
- Burr = 'Burr'
- Chi = 'Chi'
- ChiSquare = 'ChiSquare'
- Dirichlet = 'Dirichlet'
- Exponential = 'Exponential'
- FisherSnedecor = 'FisherSnedecor'
- Frechet = 'Frechet'
- Gamma = 'Gamma'
- GeneralizedPareto = 'GeneralizedPareto'
- Gumbel = 'Gumbel'
- Histogram = 'Histogram'
- InverseNormal = 'InverseNormal'
- Laplace = 'Laplace'
- LogNormal = 'LogNormal'
- LogUniform = 'LogUniform'
- Logistic = 'Logistic'
- MeixnerDistribution = 'MeixnerDistribution'
- Normal = 'Normal'
- Pareto = 'Pareto'
- Rayleigh = 'Rayleigh'
- Rice = 'Rice'
- Student = 'Student'
- Trapezoidal = 'Trapezoidal'
- Triangular = 'Triangular'
- TruncatedNormal = 'TruncatedNormal'
- Uniform = 'Uniform'
- VonMises = 'VonMises'
- WeibullMax = 'WeibullMax'
- WeibullMin = 'WeibullMin'
- class FittingCriterion(value)
Bases:
StrEnumAn enumeration.
- BIC = 'BIC'
- ChiSquared = 'ChiSquared'
- Kolmogorov = 'Kolmogorov'
- class SelectionCriterion(value)
Bases:
LowercaseStrEnumAn enumeration.
- BEST = 'best'
- FIRST = 'first'
- class SignificanceTest(value)
Bases:
StrEnumAn enumeration.
- ChiSquared = 'ChiSquared'
- Kolmogorov = 'Kolmogorov'
- compute_joint_probability(thresh, greater=True)[source]
Compute the joint probability related to a threshold.
Either \(\mathbb{P}[X \geq x]\) or \(\mathbb{P}[X \leq x]\).
- Parameters:
- Returns:
The joint probability of the different variables (by definition of the joint probability, this statistics is not computed component-wise).
- Return type:
- compute_maximum()[source]
Compute the maximum \(\text{Max}[X]\).
- compute_mean()[source]
Compute the mean \(\mathbb{E}[X]\).
- compute_minimum()[source]
Compute the \(\text{Min}[X]\).
- compute_moment(order)[source]
Compute the n-th moment \(M[X; n]\).
- compute_probability(thresh, greater=True)[source]
Compute the probability related to a threshold.
Either \(\mathbb{P}[X \geq x]\) or \(\mathbb{P}[X \leq x]\).
- Parameters:
- Returns:
The component-wise probability of the different variables.
- Return type:
- compute_quantile(prob)[source]
Compute the quantile \(\mathbb{Q}[X; \alpha]\) related to a probability.
- compute_range()[source]
Compute the range \(R[X]\).
- compute_standard_deviation()[source]
Compute the standard deviation \(\mathbb{S}[X]\).
- compute_tolerance_interval(coverage, confidence=0.95, side=ToleranceIntervalSide.BOTH)[source]
Compute a \((p,1-\alpha)\) tolerance interval \(\text{TI}[X]\).
The tolerance interval \(\text{TI}[X]\) is defined to contain at least a proportion \(p\) of the values of \(X\) with a level of confidence \(1-\alpha\). \(p\) is also called the coverage level of the TI.
Typically, \(\alpha=0.05\) or equivalently \(1-\alpha=0.95\).
The tolerance interval can be either
lower-sided (
side="LOWER": \([L, +\infty[\)),upper-sided (
side="UPPER": \(]-\infty, U]\)) orboth-sided (
side="BOTH": \([L, U]\)).
- Parameters:
coverage (float) – A minimum proportion \(p\in[0,1]\) of belonging to the TI.
confidence (float) –
A level of confidence \(1-\alpha\in[0,1]\).
By default it is set to 0.95.
side (ToleranceIntervalSide) –
The type of the tolerance interval.
By default it is set to “both”.
- Returns:
The component-wise tolerance intervals of the different variables, expressed as
{variable_name: [(lower_bound, upper_bound), ...], ... }where[(lower_bound, upper_bound), ...]are the lower and upper bounds of the tolerance interval of the different components ofvariable_name.- Return type:
See also
- compute_variance()[source]
Compute the variance \(\mathbb{V}[X]\).
- get_criteria(variable, index=0)[source]
Get the value of the fitting criterion for the different distributions.
- Parameters:
- Returns:
The value of the fitting criterion for the given variable name and component and the different distributions, as well as whether this fitting criterion is a statistical test and so this value a p-value.
- Return type:
- get_fitting_matrix()[source]
Get the fitting matrix.
This matrix contains goodness-of-fit measures for each pair < variable, distribution >.
- Returns:
The printable fitting matrix.
- Return type:
- plot(save=False, show=True, directory_path='', file_format='png')[source]
Visualize the cumulative distribution and probability density functions.
- Parameters:
save (bool) –
Whether to save the figures.
By default it is set to False.
show (bool) –
Whether to show the figures.
By default it is set to True.
directory_path (str | Path) –
The path to save the figures.
By default it is set to “”.
file_format (str) –
The file extension.
By default it is set to “png”.
- Returns:
The cumulative distribution and probability density functions for each variable.
- Return type:
- plot_criteria(variable, title='', save=False, show=True, directory='.', index=0, fig_size=(6.4, 3.2))[source]
Plot criteria for a given variable name.
- Parameters:
variable (str) – The name of the variable.
title (str) –
The title of the plot, if any.
By default it is set to “”.
save (bool) –
If
True, save the plot on the disk.By default it is set to False.
show (bool) –
If
True, show the plot.By default it is set to True.
directory (str | Path) –
The directory path, either absolute or relative.
By default it is set to “.”.
index (int) –
The index of the component of the variable.
By default it is set to 0.
fig_size (FigSizeType) –
The width and height of the figure in inches, e.g.
(w, h).By default it is set to (6.4, 3.2).
- Raises:
ValueError – If the variable is missing from the dataset.
- Return type:
Figure
- dataset: Dataset
The dataset.
- distributions: dict[str, DistributionType | list[DistributionType]]
The probability distributions of the random variables.
When a random variable is a random vector, its probability distribution is expressed as a list of marginal distributions. Otherwise, its probability distribution is expressed as the unique marginal distribution.
- fitting_criterion: FittingCriterion
The goodness-of-fit criterion, measuring how the distribution fits the data.
- level: float
The test level used by the selection criteria that are significance tests.
In statistical hypothesis testing, the test level corresponds to the risk of committing a type 1 error, that is an incorrect rejection of the null hypothesis
- n_samples: int
The number of samples.
- n_variables: int
The number of variables.
- name: str
The name of the object.
- selection_criterion: SelectionCriterion
The selection criterion to select a distribution from a list of candidates.