Ordinary Differential Equations (ODE)¶
ODE stands for Ordinary Differential Equation.
An ODEProblem represents a first order ordinary differential equation (ODE) with
a given state at an initial time.
This ODEProblem is built with a function of time and state, as well as an array
describing the intial state, and a time interval.
An ODEResult represents the solution of an ODE evaluated at a discrete set of
times within the specified time interval.
Note
This feature is under active development. Future iterations include the integration of
ODEProblem s with MDODiscipline.
Architecture¶
ODEProblem and ODEResult¶
The main classes in the ODE submodule are the ODEProblem and ODEResult.
These represent respectively the first-order ODE with its initial conditions, and the
solution of this problem evaluated at a discrete set of values for time.
As a reminder, a first-order ordinary differential equation is an equation of the form:
where \(s\) is the state which depends on \(t\), the time. The right-hand side function \(f\) is a function of the time and the state. The value of the state at an initial time \(t_0\) is known to be \(s_0\).
The solution of this problem is provided for discrete values of time within a given interval \([t_0,\ t_f]\).
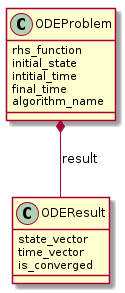
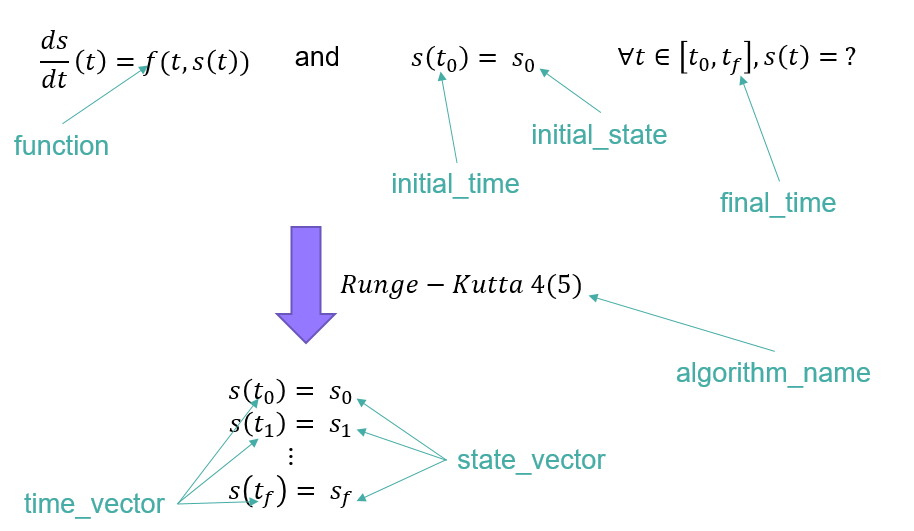
Correspondance between the elements of an ordinary differential equation with initial
conditions and the attributes of the ODEProblem and ODEResult classes.¶
Classes¶
The classes described by the ODE module are as such:
Packages¶
The submodules are organized in the following fashion.