Note
Go to the end to download the full example code
Scalable diagonal discipline¶
Let us consider the
SobieskiAerodynamics discipline.
We want to build its ScalableDiscipline counterpart,
using a ScalableDiagonalModel
For that, we can use a 20-length DiagonalDOE
and test different sizes of variables or different settings
for the scalable diagonal discipline.
from __future__ import annotations
from gemseo import configure_logger
from gemseo import create_discipline
from gemseo import create_scalable
from gemseo import create_scenario
from gemseo.problems.mdo.sobieski.core.design_space import SobieskiDesignSpace
Import¶
configure_logger()
<RootLogger root (INFO)>
Learning dataset¶
The first step is to build an AbstractFullCache dataset
from a DiagonalDOE.
Instantiate the discipline¶
For that, we instantiate the
SobieskiAerodynamics discipline
and set it up to cache all evaluations.
discipline = create_discipline("SobieskiAerodynamics")
Get the input space¶
We also define the input space on which to sample the discipline.
input_space = SobieskiDesignSpace()
input_names = [name for name in discipline.get_input_data_names() if name != "c_4"]
input_space.filter(input_names)
Build the DOE scenario¶
Lastly, we sample the discipline by means of a DOEScenario
relying on both discipline and input space.
In order to build a diagonal scalable discipline,
a DiagonalDOE must be used.
scenario = create_scenario(
[discipline], "DisciplinaryOpt", "y_2", input_space, scenario_type="DOE"
)
for output_name in discipline.get_output_data_names():
if output_name != "y_2":
scenario.add_observable(output_name)
scenario.execute({"algo": "DiagonalDOE", "n_samples": 20})
INFO - 08:56:36:
INFO - 08:56:36: *** Start DOEScenario execution ***
INFO - 08:56:36: DOEScenario
INFO - 08:56:36: Disciplines: SobieskiAerodynamics
INFO - 08:56:36: MDO formulation: DisciplinaryOpt
INFO - 08:56:36: Optimization problem:
INFO - 08:56:36: minimize y_2(x_shared, x_2, y_32, y_12)
INFO - 08:56:36: with respect to x_2, x_shared, y_12, y_32
INFO - 08:56:36: over the design space:
INFO - 08:56:36: +-------------+-------------+--------------------+-------------+-------+
INFO - 08:56:36: | Name | Lower bound | Value | Upper bound | Type |
INFO - 08:56:36: +-------------+-------------+--------------------+-------------+-------+
INFO - 08:56:36: | x_shared[0] | 0.01 | 0.05 | 0.09 | float |
INFO - 08:56:36: | x_shared[1] | 30000 | 45000 | 60000 | float |
INFO - 08:56:36: | x_shared[2] | 1.4 | 1.6 | 1.8 | float |
INFO - 08:56:36: | x_shared[3] | 2.5 | 5.5 | 8.5 | float |
INFO - 08:56:36: | x_shared[4] | 40 | 55 | 70 | float |
INFO - 08:56:36: | x_shared[5] | 500 | 1000 | 1500 | float |
INFO - 08:56:36: | x_2 | 0.75 | 1 | 1.25 | float |
INFO - 08:56:36: | y_32 | 0.235 | 0.5027962499999999 | 0.795 | float |
INFO - 08:56:36: | y_12[0] | 24850 | 50606.9742 | 77250 | float |
INFO - 08:56:36: | y_12[1] | 0.45 | 0.95 | 1.5 | float |
INFO - 08:56:36: +-------------+-------------+--------------------+-------------+-------+
INFO - 08:56:36: Solving optimization problem with algorithm DiagonalDOE:
INFO - 08:56:36: 5%|▌ | 1/20 [00:00<00:00, 164.53 it/sec, obj=[2.48500000e+04 5.75800074e+03 4.31573408e+00]]
INFO - 08:56:36: 10%|█ | 2/20 [00:00<00:00, 248.22 it/sec, obj=[2.76078947e+04 6.45112022e+03 4.27955049e+00]]
INFO - 08:56:36: 15%|█▌ | 3/20 [00:00<00:00, 301.92 it/sec, obj=[3.03657895e+04 7.17864545e+03 4.23001661e+00]]
INFO - 08:56:36: 20%|██ | 4/20 [00:00<00:00, 337.43 it/sec, obj=[3.31236842e+04 7.92362686e+03 4.18036902e+00]]
INFO - 08:56:36: 25%|██▌ | 5/20 [00:00<00:00, 364.38 it/sec, obj=[3.58815789e+04 8.66958857e+03 4.13878683e+00]]
INFO - 08:56:36: 30%|███ | 6/20 [00:00<00:00, 383.29 it/sec, obj=[3.86394737e+04 9.40253365e+03 4.10947465e+00]]
INFO - 08:56:36: 35%|███▌ | 7/20 [00:00<00:00, 399.12 it/sec, obj=[4.13973684e+04 1.01086635e+04 4.09523655e+00]]
INFO - 08:56:36: 40%|████ | 8/20 [00:00<00:00, 411.32 it/sec, obj=[4.41552632e+04 1.07748595e+04 4.09798968e+00]]
INFO - 08:56:36: 45%|████▌ | 9/20 [00:00<00:00, 421.83 it/sec, obj=[4.69131579e+04 1.13905076e+04 4.11861872e+00]]
INFO - 08:56:36: 50%|█████ | 10/20 [00:00<00:00, 428.96 it/sec, obj=[4.96710526e+04 1.19440252e+04 4.15865270e+00]]
INFO - 08:56:36: 55%|█████▌ | 11/20 [00:00<00:00, 436.67 it/sec, obj=[5.24289474e+04 1.24253852e+04 4.21950279e+00]]
INFO - 08:56:36: 60%|██████ | 12/20 [00:00<00:00, 442.43 it/sec, obj=[5.51868421e+04 1.28262516e+04 4.30264771e+00]]
INFO - 08:56:36: 65%|██████▌ | 13/20 [00:00<00:00, 448.00 it/sec, obj=[5.79447368e+04 1.31400641e+04 4.40977580e+00]]
INFO - 08:56:36: 70%|███████ | 14/20 [00:00<00:00, 452.06 it/sec, obj=[6.07026316e+04 1.33620772e+04 4.54290381e+00]]
INFO - 08:56:36: 75%|███████▌ | 15/20 [00:00<00:00, 456.74 it/sec, obj=[6.34605263e+04 1.34893612e+04 4.70448714e+00]]
INFO - 08:56:36: 80%|████████ | 16/20 [00:00<00:00, 459.88 it/sec, obj=[6.62184211e+04 1.35166373e+04 4.89903071e+00]]
INFO - 08:56:36: 85%|████████▌ | 17/20 [00:00<00:00, 463.64 it/sec, obj=[6.89763158e+04 1.34436796e+04 5.13076164e+00]]
INFO - 08:56:36: 90%|█████████ | 18/20 [00:00<00:00, 466.28 it/sec, obj=[7.17342105e+04 1.32763007e+04 5.40317758e+00]]
INFO - 08:56:36: 95%|█████████▌| 19/20 [00:00<00:00, 469.44 it/sec, obj=[7.44921053e+04 1.30407235e+04 5.71226782e+00]]
INFO - 08:56:36: 100%|██████████| 20/20 [00:00<00:00, 471.96 it/sec, obj=[7.72500000e+04 1.27392070e+04 6.06395673e+00]]
INFO - 08:56:36: Optimization result:
INFO - 08:56:36: Optimizer info:
INFO - 08:56:36: Status: None
INFO - 08:56:36: Message: None
INFO - 08:56:36: Number of calls to the objective function by the optimizer: 20
INFO - 08:56:36: Solution:
INFO - 08:56:36: Objective: 25508.372961119574
INFO - 08:56:36: Design space:
INFO - 08:56:36: +-------------+-------------+-------+-------------+-------+
INFO - 08:56:36: | Name | Lower bound | Value | Upper bound | Type |
INFO - 08:56:36: +-------------+-------------+-------+-------------+-------+
INFO - 08:56:36: | x_shared[0] | 0.01 | 0.01 | 0.09 | float |
INFO - 08:56:36: | x_shared[1] | 30000 | 30000 | 60000 | float |
INFO - 08:56:36: | x_shared[2] | 1.4 | 1.4 | 1.8 | float |
INFO - 08:56:36: | x_shared[3] | 2.5 | 2.5 | 8.5 | float |
INFO - 08:56:36: | x_shared[4] | 40 | 40 | 70 | float |
INFO - 08:56:36: | x_shared[5] | 500 | 500 | 1500 | float |
INFO - 08:56:36: | x_2 | 0.75 | 0.75 | 1.25 | float |
INFO - 08:56:36: | y_32 | 0.235 | 0.235 | 0.795 | float |
INFO - 08:56:36: | y_12[0] | 24850 | 24850 | 77250 | float |
INFO - 08:56:36: | y_12[1] | 0.45 | 0.45 | 1.5 | float |
INFO - 08:56:36: +-------------+-------------+-------+-------------+-------+
INFO - 08:56:36: *** End DOEScenario execution (time: 0:00:00.058856) ***
{'eval_jac': False, 'n_samples': 20, 'algo': 'DiagonalDOE'}
Scalable diagonal discipline¶
Build the scalable discipline¶
The second step is to build a ScalableDiscipline,
using a ScalableDiagonalModel and the database
converted to a Dataset.
dataset = scenario.to_dataset(opt_naming=False)
scalable = create_scalable("ScalableDiagonalModel", dataset)
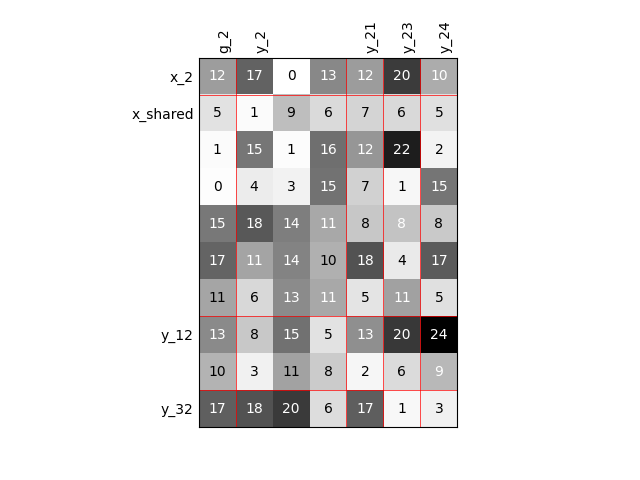
Visualize the input-output dependencies¶
We can easily access the underlying ScalableDiagonalModel
and plot the corresponding input-output dependency matrix
where the level of gray and the number (in [0,100]) represent
the degree of dependency between inputs and outputs.
Input are on the left while outputs are at the top.
More precisely, for a given output component located at the top of the graph,
these degrees are contributions to the output component and they add up to 1.
In other words, a degree expresses this contribution in percentage
and for a given column, the elements add up to 100.
scalable.scalable_model.plot_dependency(save=False, show=True)
'None'
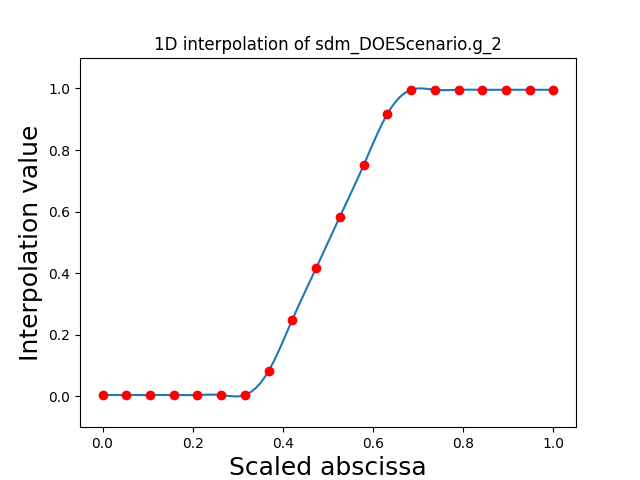
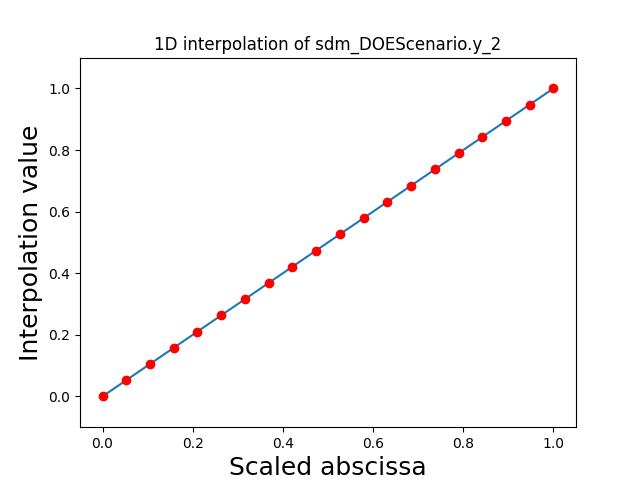
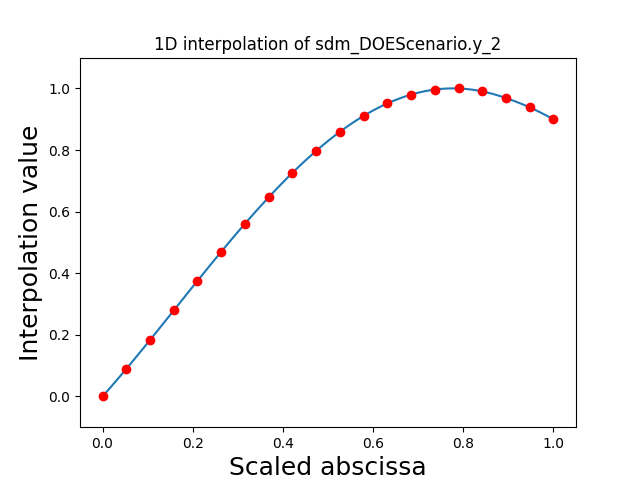
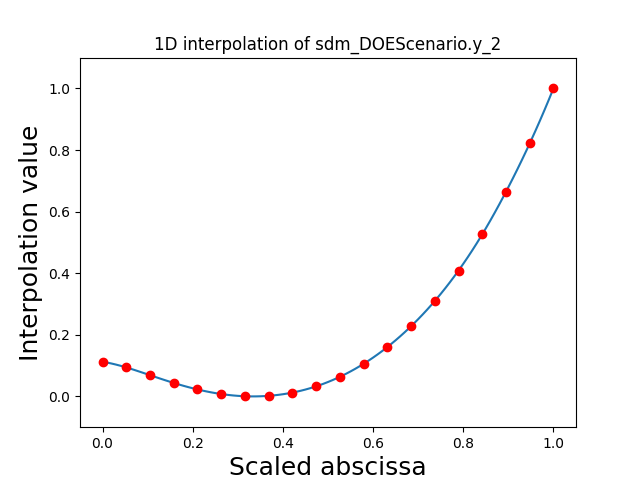
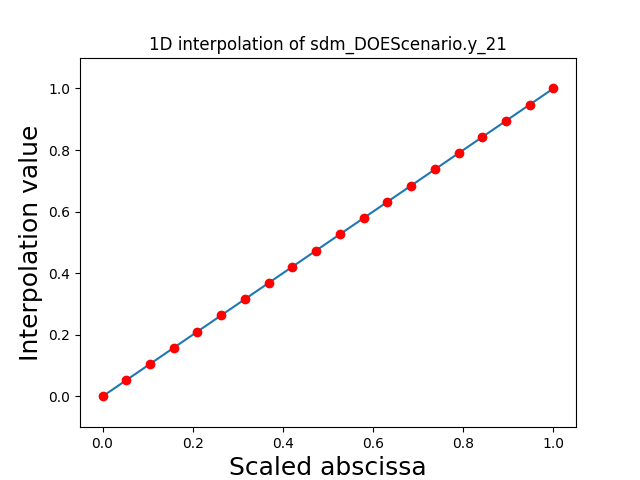
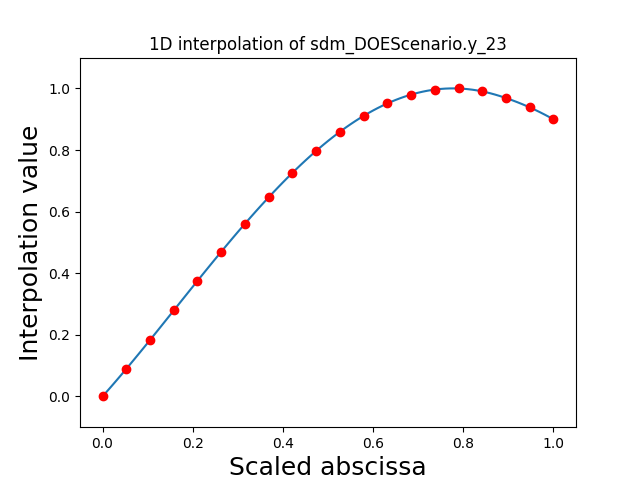
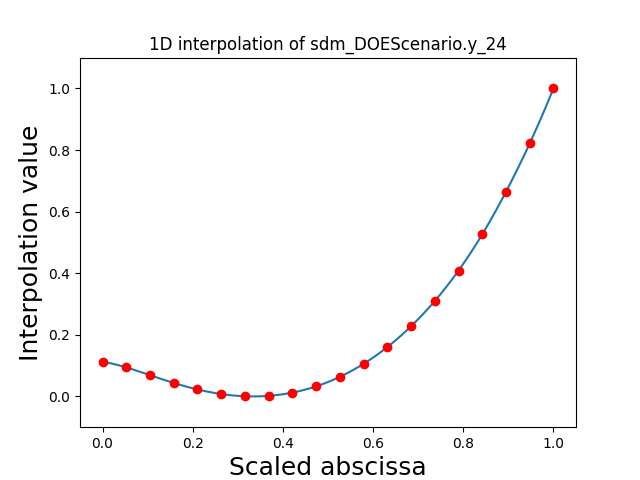
Visualize the 1D interpolations¶
For every output, we can also visualize a spline interpolation of the output samples over the diagonal of the input space.
scalable.scalable_model.plot_1d_interpolations(save=False, show=True)
[]
Increased problem dimension¶
We can repeat the construction of the scalable discipline for different sizes of variables and visualize the input-output dependency matrices.
Twice as many inputs¶
For example, we can increase the size of each input by a factor of 2.
sizes = {name: dataset.variable_names_to_n_components[name] * 2 for name in input_names}
scalable = create_scalable("ScalableDiagonalModel", dataset, sizes)
scalable.scalable_model.plot_dependency(save=False, show=True)
'None'
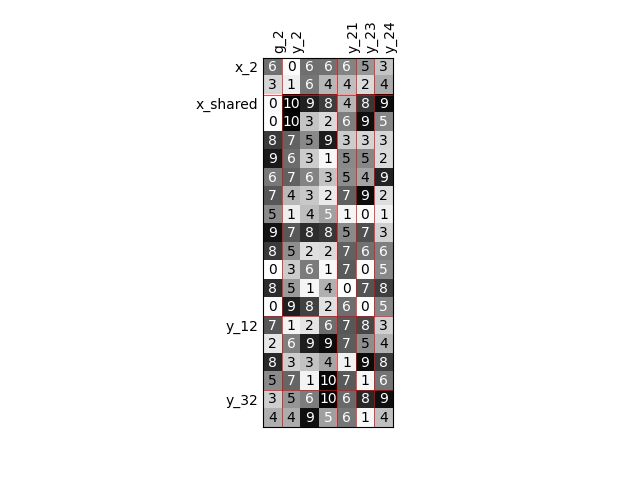
Twice as many outputs¶
Or we can increase the size of each output by a factor of 2.
sizes = {
name: discipline.cache.names_to_sizes[name] * 2
for name in discipline.get_output_data_names()
}
scalable = create_scalable("ScalableDiagonalModel", dataset, sizes)
scalable.scalable_model.plot_dependency(save=False, show=True)
'None'
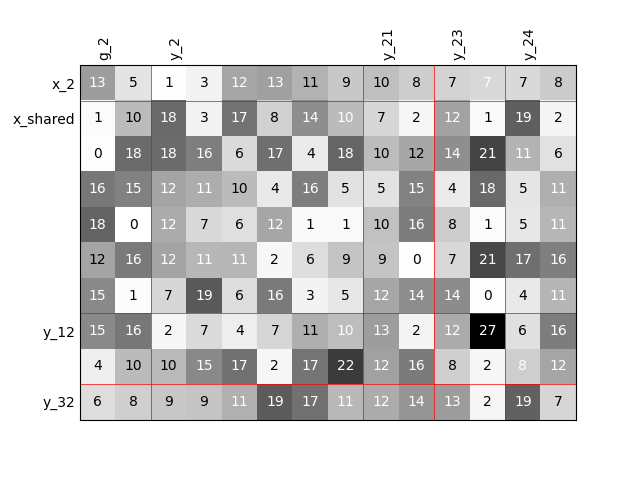
Twice as many variables¶
Or we can increase the size of each input and each output by a factor of 2.
names = input_names + list(discipline.get_output_data_names())
sizes = {name: dataset.variable_names_to_n_components[name] * 2 for name in names}
scalable = create_scalable("ScalableDiagonalModel", dataset, sizes)
scalable.scalable_model.plot_dependency(save=False, show=True)

'None'
Binary IO dependencies¶
By default, any output component depends on any input component with a random level. We can also consider sparser input-output dependency by means of binary input-output dependency matrices. For that, we have to set the value of the fill factor which represents the part of connection between inputs and outputs. Then, a connection is represented by a black square while an absence of connection is presented by a white one. When the fill factor is equal to 1, any input is connected to any output. Conversely, when the fill factor is equal to 0, there is not a single connection between inputs and outputs.
Fill factor = 0.2¶
scalable = create_scalable("ScalableDiagonalModel", dataset, sizes, fill_factor=0.2)
scalable.scalable_model.plot_dependency(save=False, show=True)
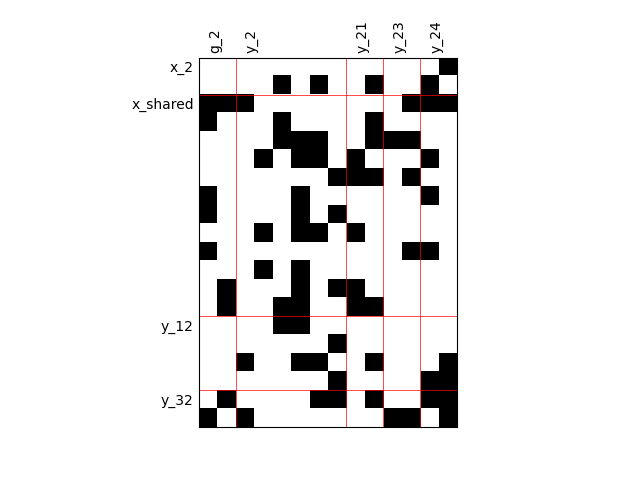
'None'
Fill factor = 0.5¶
scalable = create_scalable("ScalableDiagonalModel", dataset, sizes, fill_factor=0.5)
scalable.scalable_model.plot_dependency(save=False, show=True)
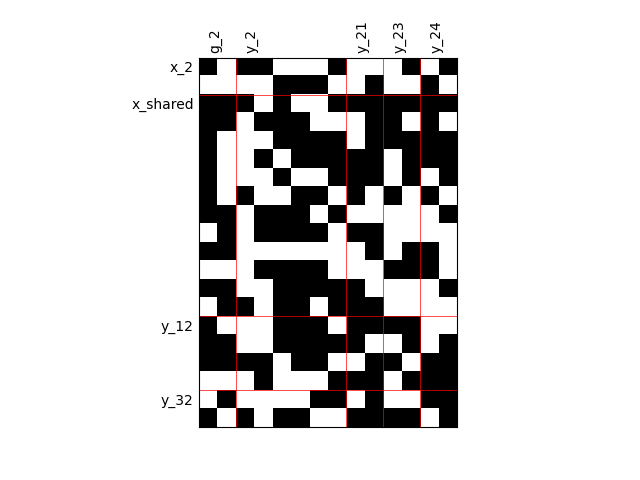
'None'
Fill factor = 0.8¶
scalable = create_scalable("ScalableDiagonalModel", dataset, sizes, fill_factor=0.8)
scalable.scalable_model.plot_dependency(save=False, show=True)
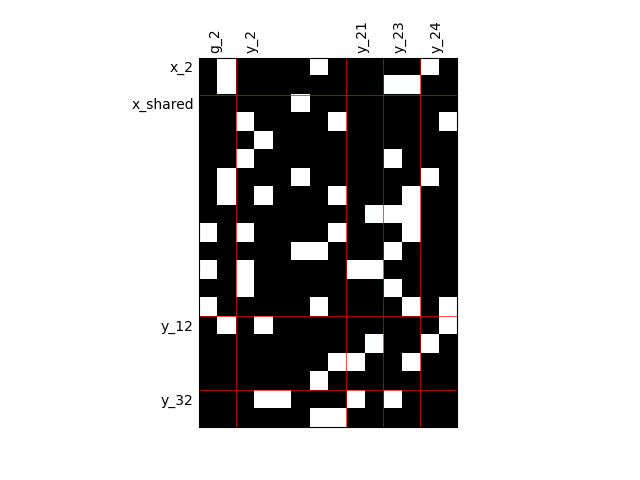
'None'
Heterogeneous dependencies¶
scalable = create_scalable(
"ScalableDiagonalModel", dataset, sizes, fill_factor={"y_2": 0.2}
)
scalable.scalable_model.plot_dependency(save=False, show=True)

'None'
Group dependencies¶
scalable = create_scalable(
"ScalableDiagonalModel", dataset, sizes, group_dep={"y_2": ["x_shared"]}
)
scalable.scalable_model.plot_dependency(save=False, show=True)
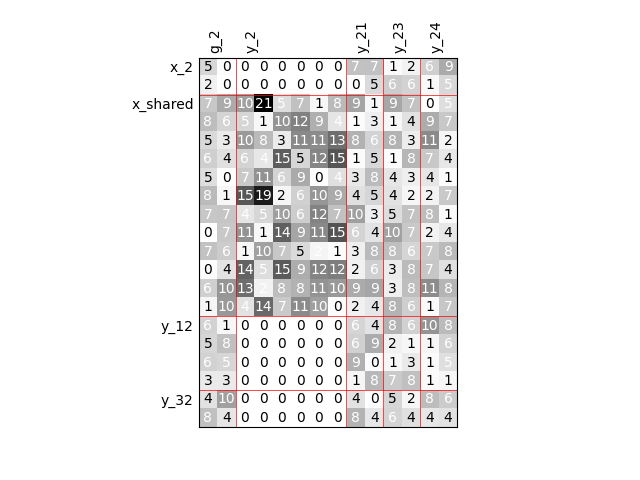
'None'
Total running time of the script: (0 minutes 3.544 seconds)