Quadratic approximations¶
Preliminaries: instantiation and execution of the MDO scenario¶
Let’s start with the following code lines which instantiate and execute the MDOScenario :
from gemseo.api import create_discipline, create_scenario
formulation = 'MDF'
disciplines = create_discipline(["SobieskiPropulsion", "SobieskiAerodynamics",
"SobieskiMission", "SobieskiStructure"])
scenario = create_scenario(disciplines,
formulation=formulation,
objective_name="y_4",
maximize_objective=True,
design_space="design_space.txt")
scenario.set_differentiation_method("user")
algo_options = {'max_iter': 10, 'algo': "SLSQP"}
for constraint in ["g_1","g_2","g_3"]:
scenario.add_constraint(constraint, 'ineq')
scenario.execute(algo_options)
To plot the quadratic approximations, use the API method execute_post()
with the keyword “QuadApprox” and
additional arguments concerning the type of display (file, screen, both):
scenario.post_process(“QuadApprox”, save=True, show=False, file_path=“mdf”)
QuadApprox¶
Description¶
The QuadApprox post processing
performs a quadratic approximation of a given function
from an optimization history
and plot the results as cuts of the approximation.
The function index can be passed as option. It is possible either to save the plot, to show the plot or both.
Options¶
extension,
str- file extensionfile_path,
str- the base paths of the files to exportfunc_index,
int- functional indexfunction,
str- function name to build quadratic approximationsave,
bool- if True, exports plot to pdfshow,
bool- if True, displays the plot windows
Case of the MDF formulation¶
The quadratic approximations are triggered by the following command:
scenario.post_process(“QuadApprox”, save=False, show=True, function=“-y_4”, file_path=“mdf”)
The figure Hessian approximation on the Sobieski use case for the MDF formulation shows an approximation of the Hessian matrix \(\frac{\partial^2 f}{\partial x_i \partial x_j}\) based on the Symmetric Rank 1 method (SR1) [NW06]. The color map uses a symmetric logarithmic (symlog) scale. This plots the crossed influence of the design variables on the objective function or constraints. For instance, on the last figure, the maximal second order sensitivity is \(\frac{\partial^2 -y_4}{\partial^2 x_0} = 2.10^5\), which means that the \(x_0\) is the most influent variable. Then, the crossed derivative \(\frac{\partial^2 -y_4}{\partial x_0 \partial x_2} = 5.10^4\) is positive and relatively high compared to the previous one but the combined effects of \(x_0\) and \(x_2\) are non-negligible in comparison.
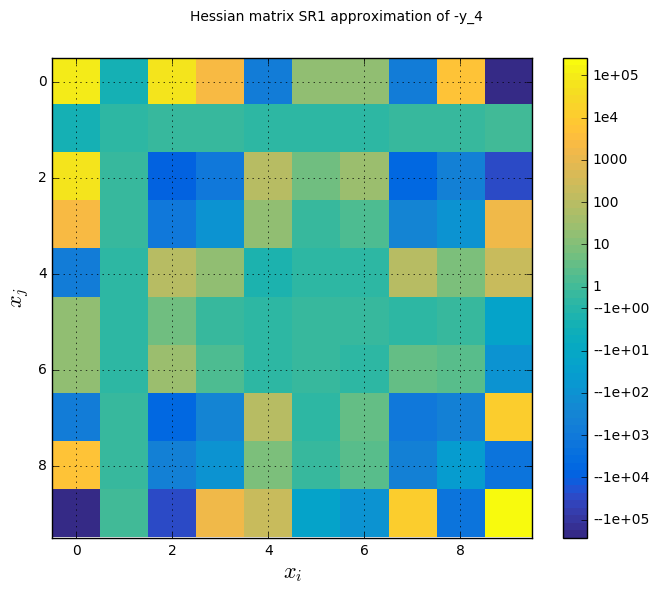
Hessian approximation on the Sobieski use case for the MDF formulation¶
The figure Quadratic approximation on the Sobieski use case for the MDF formulation represents the quadratic approximation of the objective around the optimal solution : \(a_{i}(t)=0.5 (t-x^*_i)^2 \frac{\partial^2 f}{\partial x_i^2} + (t-x^*_i) \frac{\partial f}{\partial x_i} + f(x^*)\), where \(x^*\) is the optimal solution. This approximation highlights the sensitivity of the objective function with respect to the design variables: we notice that the design variables \(x\_1, x\_5, x\_6\) have little influence , whereas \(x\_0, x\_2, x\_9\) have a huge influence on the objective. This trend is also noted in the diagonal terms of the hessian matrix \(\frac{\partial^2 f}{\partial x_i^2}\).
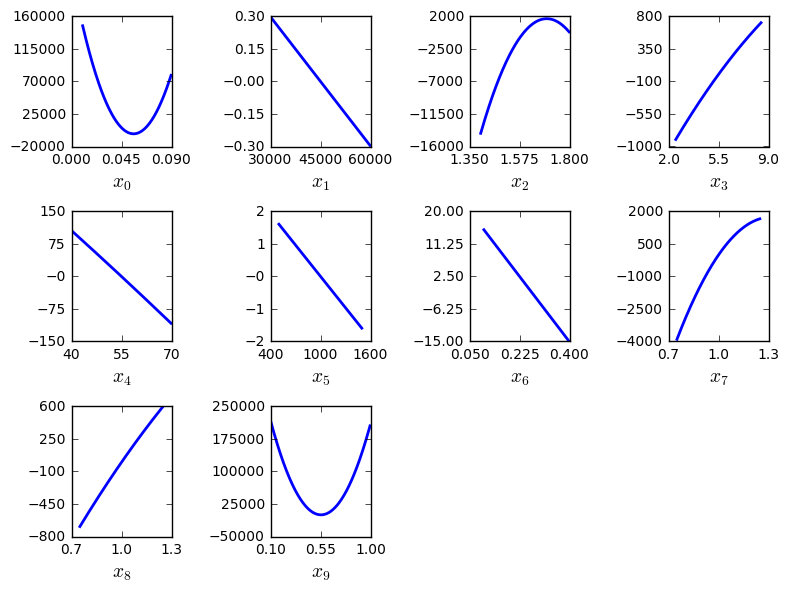
Quadratic approximation on the Sobieski use case for the MDF formulation¶
Case of the IDF formulation¶
The quadratic approximations are triggered by the following command:
scenario.post_process(“QuadApprox”, save=False, show=True, function=“-y_4”, file_path=“idf”)
Figure Hessian approximation on the Sobieski use case for the IDF formulation shows an approximation of the Hessian matrix \(\frac{\partial^2 f}{\partial x_i \partial x_j}\) based on the Symmetric Rank 1 method (SR1) [NW06]. The color map uses a symmetric logarithmic (symlog) scale.
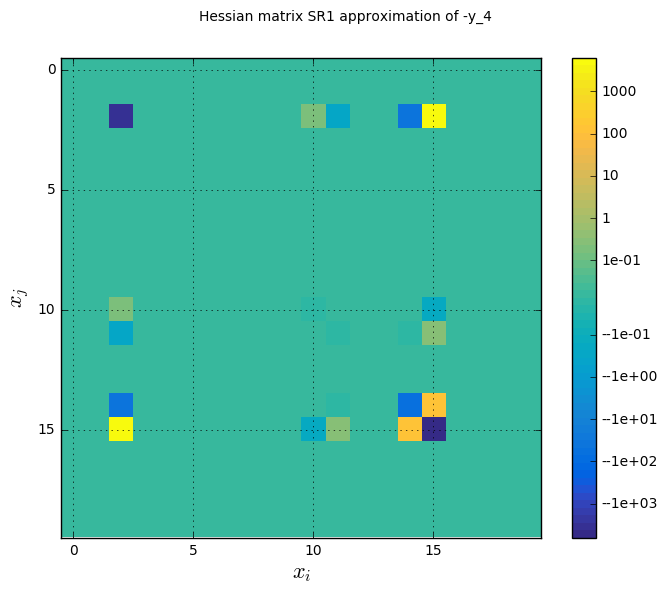
Hessian approximation on the Sobieski use case for the IDF formulation¶
In Quadratic approximations on the Sobieski use case for the IDF formulation, the 20 plots represent the quadratic approximations of the objective around the optimal solution. Unlike (), the Mach number \(x_6\) is the only of the problem that has an influence on the optimum, because it is the only that occurs in objective function’s formula.
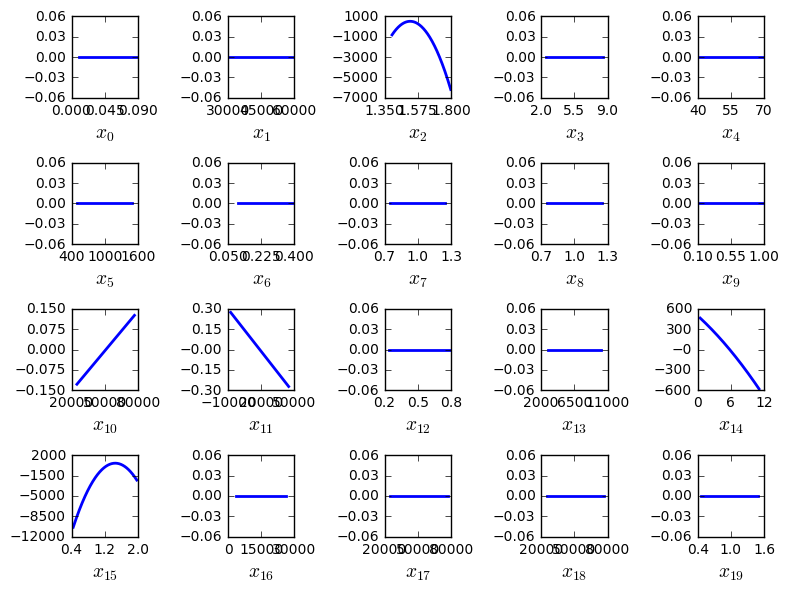
Quadratic approximations on the Sobieski use case for the IDF formulation¶
