analysis module¶
Class for the estimation of Sobol’ indices.
Let us consider the model \(Y=f(X_1,\ldots,X_d)\) where:
\(X_1,\ldots,X_d\) are independent random variables,
\(E\left[f(X_1,\ldots,X_d)^2\right]<\infty\).
Then, the following decomposition is unique:
where:
\(f_0=E[Y]\),
\(f_i(X_i)=E[Y|X_i]-f_0\),
\(f_{i,j}(X_i,X_j)=E[Y|X_i,X_j]-f_i(X_i)-f_j(X_j)-f_0\)
and so on.
Then, the shift to variance leads to:
and the Sobol’ indices are obtained by dividing by the variance and sum up to 1:
A Sobol’ index represents the share of output variance explained by a parameter or a group of parameters. For the parameter \(X_i\),
\(S_i\) is the first-order Sobol’ index measuring the individual effect of \(X_i\),
\(S_{i,j}\) is the second-order Sobol’ index measuring the joint effect between \(X_i\) and \(X_j\),
\(S_{i,j,k}\) is the third-order Sobol’ index measuring the joint effect between \(X_i\), \(X_j\) and \(X_k\),
and so on.
In practice, we only consider the first-order Sobol’ index:
and the total-order Sobol’ index:
The latter represents the sum of the individual effect of \(X_i\) and the joint effects between \(X_i\) and any parameter or group of parameters.
This methodology relies on the SobolAnalysis class. Precisely,
SobolAnalysis.indices contains
both SobolAnalysis.first_order_indices and
SobolAnalysis.total_order_indices
while SobolAnalysis.main_indices represents total-order Sobol’
indices.
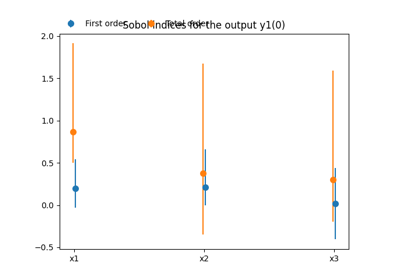
Lastly, the SobolAnalysis.plot() method represents
the estimations of both first-order and total-order Sobol’ indices along with
their 95% confidence interval.
The user can select the algorithm to estimate the Sobol’ indices. The computation relies on OpenTURNS capabilities.
- class gemseo.uncertainty.sensitivity.sobol.analysis.SobolAnalysis(disciplines, parameter_space, n_samples, output_names=None, algo=None, algo_options=None, formulation='MDF', **formulation_options)[source]¶
Bases:
SensitivityAnalysisSensitivity analysis based on the Sobol’ indices.
Examples
>>> from numpy import pi >>> from gemseo.api import create_discipline, create_parameter_space >>> from gemseo.uncertainty.sensitivity.sobol.analysis import SobolAnalysis >>> >>> expressions = {"y": "sin(x1)+7*sin(x2)**2+0.1*x3**4*sin(x1)"} >>> discipline = create_discipline( ... "AnalyticDiscipline", expressions=expressions ... ) >>> >>> parameter_space = create_parameter_space() >>> parameter_space.add_random_variable( ... "x1", "OTUniformDistribution", minimum=-pi, maximum=pi ... ) >>> parameter_space.add_random_variable( ... "x2", "OTUniformDistribution", minimum=-pi, maximum=pi ... ) >>> parameter_space.add_random_variable( ... "x3", "OTUniformDistribution", minimum=-pi, maximum=pi ... ) >>> >>> analysis = SobolAnalysis([discipline], parameter_space, n_samples=10000) >>> indices = analysis.compute_indices()
- Parameters:
disciplines (Collection[MDODiscipline]) – The discipline or disciplines to use for the analysis.
parameter_space (ParameterSpace) – A parameter space.
n_samples (int) – A number of samples. If
None, the number of samples is computed by the algorithm.output_names (Iterable[str] | None) – The disciplines’ outputs to be considered for the analysis. If
None, use all the outputs.algo (str | None) – The name of the DOE algorithm. If
None, use theSensitivityAnalysis.DEFAULT_DRIVER.algo_options (Mapping[str, DOELibraryOptionType] | None) – The options of the DOE algorithm.
formulation (str) –
The name of the
MDOFormulationto sample the disciplines.By default it is set to “MDF”.
**formulation_options (Any) – The options of the
MDOFormulation.
- compute_indices(outputs=None, algo='Saltelli')[source]¶
- Parameters:
- Returns:
The sensitivity indices.
With the following structure:
{ "method_name": { "output_name": [ { "input_name": data_array, } ] } }
- Return type:
- export_to_dataset()¶
Convert
SensitivityAnalysis.indicesinto aDataset.- Returns:
The sensitivity indices.
- Return type:
- get_intervals(first_order=True)[source]¶
Get the confidence interval for Sobol’ indices.
- Parameters:
first_order (bool) –
The type of indices. If True, returns the intervals for the first-order indices. Otherwise, for the total-order indices.
By default it is set to True.
- Returns:
The confidence intervals for the Sobol’ indices.
With the following structure:
{ "output_name": [ { "input_name": data_array, } ] }
- Return type:
- static load(file_path)¶
Load a sensitivity analysis from the disk.
- Parameters:
file_path (str | Path) – The path to the file.
- Returns:
The sensitivity analysis.
- Return type:
- plot(output, inputs=None, title=None, save=True, show=False, file_path=None, directory_path=None, file_name=None, file_format=None, sort=True, sort_by_total=True)[source]¶
Plot the first- and total-order Sobol’ indices.
For \(i\in\{1,\ldots,d\}\), plot \(S_i^{1}\) and \(S_T^{1}\) with their confidence intervals.
- Parameters:
output (str | tuple[str, int]) – The output for which to display sensitivity indices, either a name or a tuple of the form (name, component). If name, its first component is considered.
inputs (Iterable[str] | None) – The inputs to display. If None, display all.
title (str | None) – The title of the plot. If None, no title.
save (bool) –
If True, save the figure.
By default it is set to True.
show (bool) –
If True, show the figure.
By default it is set to False.
file_path (str | Path | None) – A file path. Either a complete file path, a directory name or a file name. If None, use a default file name and a default directory. The file extension is inferred from filepath extension, if any.
directory_path (str | Path | None) – The description is missing.
file_name (str | None) – The description is missing.
file_format (str | None) – A file format, e.g. ‘png’, ‘pdf’, ‘svg’, … Used when
file_pathdoes not have any extension. If None, use a default file extension.sort (bool) –
The sorting option. If True, sort variables before display.
By default it is set to True.
sort_by_total (bool) –
The type of sorting. If True, sort variables according to total-order Sobol’ indices. Otherwise, use first-order Sobol’ indices.
By default it is set to True.
- plot_bar(outputs, inputs=None, standardize=False, title=None, save=True, show=False, file_path=None, directory_path=None, file_name=None, file_format=None, **options)¶
Plot the sensitivity indices on a bar chart.
This method may consider one or more outputs, as well as all inputs (default behavior) or a subset.
- Parameters:
outputs (OutputsType) – The outputs for which to display sensitivity indices, either a name, a list of names, a (name, component) tuple, a list of such tuples or a list mixing such tuples and names. When a name is specified, all its components are considered. If None, use the default outputs.
inputs (Iterable[str] | None) – The inputs to display. If None, display all.
standardize (bool) –
If True, standardize the indices between 0 and 1 for each output.
By default it is set to False.
title (str | None) – The title of the plot. If None, no title.
save (bool) –
If True, save the figure.
By default it is set to True.
show (bool) –
If True, show the figure.
By default it is set to False.
file_path (str | Path | None) – The path of the file to save the figures. If the extension is missing, use
file_extension. If None, create a file path fromdirectory_path,file_nameandfile_extension.directory_path (str | Path | None) – The path of the directory to save the figures. If None, use the current working directory.
file_name (str | None) – The name of the file to save the figures. If None, use a default one generated by the post-processing.
file_format (str | None) – A file extension, e.g. ‘png’, ‘pdf’, ‘svg’, … If None, use a default file extension.
options (int) –
- Returns:
A bar chart representing the sensitivity indices.
- Return type:
- plot_comparison(indices, output, inputs=None, title=None, use_bar_plot=True, save=True, show=False, file_path=None, directory_path=None, file_name=None, file_format=None, **options)¶
Plot a comparison between the current sensitivity indices and other ones.
This method allows to use either a bar chart (default option) or a radar one.
- Parameters:
indices (list[SensitivityAnalysis]) – The sensitivity indices.
output (str | tuple[str, int]) – The output for which to display sensitivity indices, either a name or a tuple of the form (name, component). If name, its first component is considered.
inputs (Iterable[str] | None) – The inputs to display. If None, display all.
title (str | None) – The title of the plot. If None, no title.
use_bar_plot (bool) –
The type of graph. If True, use a bar plot. Otherwise, use a radar chart.
By default it is set to True.
save (bool) –
If True, save the figure.
By default it is set to True.
show (bool) –
If True, show the figure.
By default it is set to False.
file_path (str | Path | None) – The path of the file to save the figures. If None, create a file path from
directory_path,file_nameandfile_format.directory_path (str | Path | None) – The path of the directory to save the figures. If None, use the current working directory.
file_name (str | None) – The name of the file to save the figures. If None, use a default one generated by the post-processing.
file_format (str | None) – A file format, e.g. ‘png’, ‘pdf’, ‘svg’, … If None, use a default file extension.
**options (bool) – The options passed to the underlying
DatasetPlot.
- Returns:
A graph comparing sensitivity indices.
- Return type:
- plot_field(output, mesh=None, inputs=None, standardize=False, title=None, save=True, show=False, file_path=None, directory_path=None, file_name=None, file_format=None, properties=None)¶
Plot the sensitivity indices related to a 1D or 2D functional output.
The output is considered as a 1D or 2D functional variable, according to the shape of the mesh on which it is represented.
- Parameters:
output (str | tuple[str, int]) – The output for which to display sensitivity indices, either a name or a tuple of the form (name, component) where (name, component) is used to sort the inputs. If name, its first component is considered.
mesh (ndarray | None) – The mesh on which the p-length output is represented. Either a p-length array for a 1D functional output or a (p, 2) array for a 2D one. If None, assume a 1D functional output.
inputs (Iterable[str] | None) – The inputs to display. If None, display all inputs.
standardize (bool) –
If True, standardize the indices between 0 and 1 for each output.
By default it is set to False.
title (str | None) – The title of the plot. If None, no title is displayed.
save (bool) –
If True, save the figure.
By default it is set to True.
show (bool) –
If True, show the figure.
By default it is set to False.
file_path (str | Path | None) – The path of the file to save the figures. If None, create a file path from
directory_path,file_nameandfile_extension.directory_path (str | Path | None) – The path of the directory to save the figures. If None, use the current working directory.
file_name (str | None) – The name of the file to save the figures. If None, use a default one generated by the post-processing.
file_format (str | None) – A file extension, e.g. ‘png’, ‘pdf’, ‘svg’, … If None, use a default file extension.
properties (Mapping[str, DatasetPlotPropertyType]) – The general properties of a
DatasetPlot.
- Returns:
A bar plot representing the sensitivity indices.
- Raises:
NotImplementedError – If the dimension of the mesh is greater than 2.
- Return type:
- plot_radar(outputs, inputs=None, standardize=False, title=None, save=True, show=False, file_path=None, directory_path=None, file_name=None, file_format=None, min_radius=None, max_radius=None, **options)¶
Plot the sensitivity indices on a radar chart.
This method may consider one or more outputs, as well as all inputs (default behavior) or a subset.
For visualization purposes, it is also possible to change the minimum and maximum radius values.
- Parameters:
outputs (OutputsType) – The outputs for which to display sensitivity indices, either a name, a list of names, a (name, component) tuple, a list of such tuples or a list mixing such tuples and names. When a name is specified, all its components are considered. If None, use the default outputs.
inputs (Iterable[str] | None) – The inputs to display. If None, display all.
standardize (bool) –
If True, standardize the indices between 0 and 1 for each output.
By default it is set to False.
title (str | None) – The title of the plot. If None, no title.
save (bool) –
If True, save the figure.
By default it is set to True.
show (bool) –
If True, show the figure.
By default it is set to False.
file_path (str | Path | None) – The path of the file to save the figures. If the extension is missing, use
file_extension. If None, create a file path fromdirectory_path,file_nameandfile_extension.directory_path (str | Path | None) – The path of the directory to save the figures. If None, use the current working directory.
file_name (str | None) – The name of the file to save the figures. If None, use a default one generated by the post-processing.
file_format (str | None) – A file extension, e.g. ‘png’, ‘pdf’, ‘svg’, … If None, use a default file extension.
min_radius (float | None) – The minimal radial value. If None, from data.
max_radius (float | None) – The maximal radial value. If None, from data.
options (bool) –
- Returns:
A radar chart representing the sensitivity indices.
- Return type:
- save(file_path)¶
Save the current sensitivity analysis on the disk.
- Parameters:
file_path (str | Path) – The path to the file.
- Return type:
None
- sort_parameters(output)¶
Return the parameters sorted in descending order.
- Parameters:
output (str | tuple[str, int]) – An output of the form
(name, component), where name is the output name and component is the output component. If a string is passed, the tuple(name, 0)will be considered corresponding to the first component of the outputname.- Returns:
The input parameters sorted in descending order.
- Return type:
- static standardize_indices(indices)¶
Standardize the sensitivity indices for each output component.
Each index is replaced by its absolute value divided by the largest index. Thus, the standardized indices belong to the interval \([0,1]\).
- AVAILABLE_ALGOS = ['Jansen', 'Martinez', 'MauntzKucherenko', 'Saltelli']¶
- DEFAULT_DRIVER = 'OT_SOBOL_INDICES'¶
- property first_order_indices: Dict[str, List[Dict[str, ndarray]]]¶
The first-order Sobol’ indices.
With the following structure:
{ "output_name": [ { "input_name": data_array, } ] }
- Type:
- property indices: dict[str, Dict[str, List[Dict[str, numpy.ndarray]]]]¶
The sensitivity indices.
With the following structure:
{ "method_name": { "output_name": [ { "input_name": data_array, } ] } }