Variables influence¶

In this example, we illustrate the use of the VariableInfluence plot on the Sobieski’s SSBJ problem.

from __future__ import annotations

from gemseo.api import configure_logger
from gemseo.api import create_discipline
from gemseo.api import create_scenario
from gemseo.problems.sobieski.core.problem import SobieskiProblem

Import¶

The first step is to import some functions from the API and a method to get the design space.

configure_logger()

<RootLogger root (INFO)>

Description¶

The VariableInfluence post-processing performs first-order variable influence analysis.

The method computes \(\frac{d f}{d x_i} \cdot \left(x_{i_*} - x_{initial_design}\right)\), where \(x_{initial_design}\) is the initial value of the variable and \(x_{i_*}\) is the optimal value of the variable.

Create disciplines¶

At this point, we instantiate the disciplines of Sobieski’s SSBJ problem: Propulsion, Aerodynamics, Structure and Mission

disciplines = create_discipline(
    [
        "SobieskiPropulsion",
        "SobieskiAerodynamics",
        "SobieskiStructure",
        "SobieskiMission",
    ]
)

Create design space¶

We also read the design space from the SobieskiProblem.

design_space = SobieskiProblem().design_space

Create and execute scenario¶

The next step is to build an MDO scenario in order to maximize the range, encoded ‘y_4’, with respect to the design parameters, while satisfying the inequality constraints ‘g_1’, ‘g_2’ and ‘g_3’. We can use the MDF formulation, the SLSQP optimization algorithm and a maximum number of iterations equal to 100.

scenario = create_scenario(
    disciplines,
    formulation="MDF",
    objective_name="y_4",
    maximize_objective=True,
    design_space=design_space,
)
scenario.set_differentiation_method()
for constraint in ["g_1", "g_2", "g_3"]:
    scenario.add_constraint(constraint, "ineq")
scenario.execute({"algo": "SLSQP", "max_iter": 10})

    INFO - 16:55:47:
    INFO - 16:55:47: *** Start MDOScenario execution ***
    INFO - 16:55:47: MDOScenario
    INFO - 16:55:47:    Disciplines: SobieskiAerodynamics SobieskiMission SobieskiPropulsion SobieskiStructure
    INFO - 16:55:47:    MDO formulation: MDF
    INFO - 16:55:47: Optimization problem:
    INFO - 16:55:47:    minimize -y_4(x_shared, x_1, x_2, x_3) = -y_4(x_shared, x_1, x_2, x_3)
    INFO - 16:55:47:    with respect to x_1, x_2, x_3, x_shared
    INFO - 16:55:47:    subject to constraints:
    INFO - 16:55:47:       g_1(x_shared, x_1, x_2, x_3) <= 0.0
    INFO - 16:55:47:       g_2(x_shared, x_1, x_2, x_3) <= 0.0
    INFO - 16:55:47:       g_3(x_shared, x_1, x_2, x_3) <= 0.0
    INFO - 16:55:47:    over the design space:
    INFO - 16:55:47:    +-------------+-------------+-------+-------------+-------+
    INFO - 16:55:47:    | name        | lower_bound | value | upper_bound | type  |
    INFO - 16:55:47:    +-------------+-------------+-------+-------------+-------+
    INFO - 16:55:47:    | x_shared[0] |     0.01    |  0.05 |     0.09    | float |
    INFO - 16:55:47:    | x_shared[1] |    30000    | 45000 |    60000    | float |
    INFO - 16:55:47:    | x_shared[2] |     1.4     |  1.6  |     1.8     | float |
    INFO - 16:55:47:    | x_shared[3] |     2.5     |  5.5  |     8.5     | float |
    INFO - 16:55:47:    | x_shared[4] |      40     |   55  |      70     | float |
    INFO - 16:55:47:    | x_shared[5] |     500     |  1000 |     1500    | float |
    INFO - 16:55:47:    | x_1[0]      |     0.1     |  0.25 |     0.4     | float |
    INFO - 16:55:47:    | x_1[1]      |     0.75    |   1   |     1.25    | float |
    INFO - 16:55:47:    | x_2         |     0.75    |   1   |     1.25    | float |
    INFO - 16:55:47:    | x_3         |     0.1     |  0.5  |      1      | float |
    INFO - 16:55:47:    +-------------+-------------+-------+-------------+-------+
    INFO - 16:55:47: Solving optimization problem with algorithm SLSQP:
    INFO - 16:55:47: ...   0%|          | 0/10 [00:00<?, ?it]
    INFO - 16:55:47: ...  10%|█         | 1/10 [00:00<00:00, 11.33 it/sec, obj=-536]
    INFO - 16:55:47: ...  20%|██        | 2/10 [00:00<00:00,  8.84 it/sec, obj=-2.12e+3]
 WARNING - 16:55:48: MDAJacobi has reached its maximum number of iterations but the normed residual 1.4486313079508508e-06 is still above the tolerance 1e-06.
    INFO - 16:55:48: ...  30%|███       | 3/10 [00:00<00:00,  7.69 it/sec, obj=-3.75e+3]
    INFO - 16:55:48: ...  40%|████      | 4/10 [00:00<00:00,  7.51 it/sec, obj=-4.01e+3]
 WARNING - 16:55:48: MDAJacobi has reached its maximum number of iterations but the normed residual 2.928004141058104e-06 is still above the tolerance 1e-06.
    INFO - 16:55:48: ...  50%|█████     | 5/10 [00:00<00:00,  7.15 it/sec, obj=-4.49e+3]
    INFO - 16:55:48: ...  60%|██████    | 6/10 [00:00<00:00,  7.27 it/sec, obj=-3.4e+3]
    INFO - 16:55:48: ...  70%|███████   | 7/10 [00:00<00:00,  7.91 it/sec, obj=-4.93e+3]
    INFO - 16:55:48: ...  80%|████████  | 8/10 [00:00<00:00,  8.24 it/sec, obj=-4.76e+3]
    INFO - 16:55:48: ...  90%|█████████ | 9/10 [00:01<00:00,  8.58 it/sec, obj=-4.62e+3]
    INFO - 16:55:48: ... 100%|██████████| 10/10 [00:01<00:00,  8.95 it/sec, obj=-4.56e+3]
    INFO - 16:55:48: Optimization result:
    INFO - 16:55:48:    Optimizer info:
    INFO - 16:55:48:       Status: None
    INFO - 16:55:48:       Message: Maximum number of iterations reached. GEMSEO Stopped the driver
    INFO - 16:55:48:       Number of calls to the objective function by the optimizer: 12
    INFO - 16:55:48:    Solution:
    INFO - 16:55:48:       The solution is feasible.
    INFO - 16:55:48:       Objective: -3749.8868975554387
    INFO - 16:55:48:       Standardized constraints:
    INFO - 16:55:48:          g_1 = [-0.01671296 -0.03238836 -0.04350867 -0.05123129 -0.05681738 -0.13780658
    INFO - 16:55:48:  -0.10219342]
    INFO - 16:55:48:          g_2 = -0.0004062839430756249
    INFO - 16:55:48:          g_3 = [-0.66482546 -0.33517454 -0.11023156 -0.183255  ]
    INFO - 16:55:48:       Design space:
    INFO - 16:55:48:       +-------------+-------------+---------------------+-------------+-------+
    INFO - 16:55:48:       | name        | lower_bound |        value        | upper_bound | type  |
    INFO - 16:55:48:       +-------------+-------------+---------------------+-------------+-------+
    INFO - 16:55:48:       | x_shared[0] |     0.01    | 0.05989842901423112 |     0.09    | float |
    INFO - 16:55:48:       | x_shared[1] |    30000    |  59853.73840058666  |    60000    | float |
    INFO - 16:55:48:       | x_shared[2] |     1.4     |         1.4         |     1.8     | float |
    INFO - 16:55:48:       | x_shared[3] |     2.5     |  2.527371250092273  |     8.5     | float |
    INFO - 16:55:48:       | x_shared[4] |      40     |  69.86825198198687  |      70     | float |
    INFO - 16:55:48:       | x_shared[5] |     500     |  1495.734648986894  |     1500    | float |
    INFO - 16:55:48:       | x_1[0]      |     0.1     |         0.4         |     0.4     | float |
    INFO - 16:55:48:       | x_1[1]      |     0.75    |  0.7521124139939552 |     1.25    | float |
    INFO - 16:55:48:       | x_2         |     0.75    |  0.7520888531444992 |     1.25    | float |
    INFO - 16:55:48:       | x_3         |     0.1     |  0.1398000762238233 |      1      | float |
    INFO - 16:55:48:       +-------------+-------------+---------------------+-------------+-------+
    INFO - 16:55:48: *** End MDOScenario execution (time: 0:00:01.134518) ***

{'max_iter': 10, 'algo': 'SLSQP'}

Post-process scenario¶

Lastly, we post-process the scenario by means of the BasicHistory plot.

Tip

Each post-processing method requires different inputs and offers a variety of customization options. Use the API function get_post_processing_options_schema() to print a table with the options for any post-processing algorithm. Or refer to our dedicated page: Post-processing algorithms.

scenario.post_process("VariableInfluence", fig_size=(15, 12), save=False, show=True)

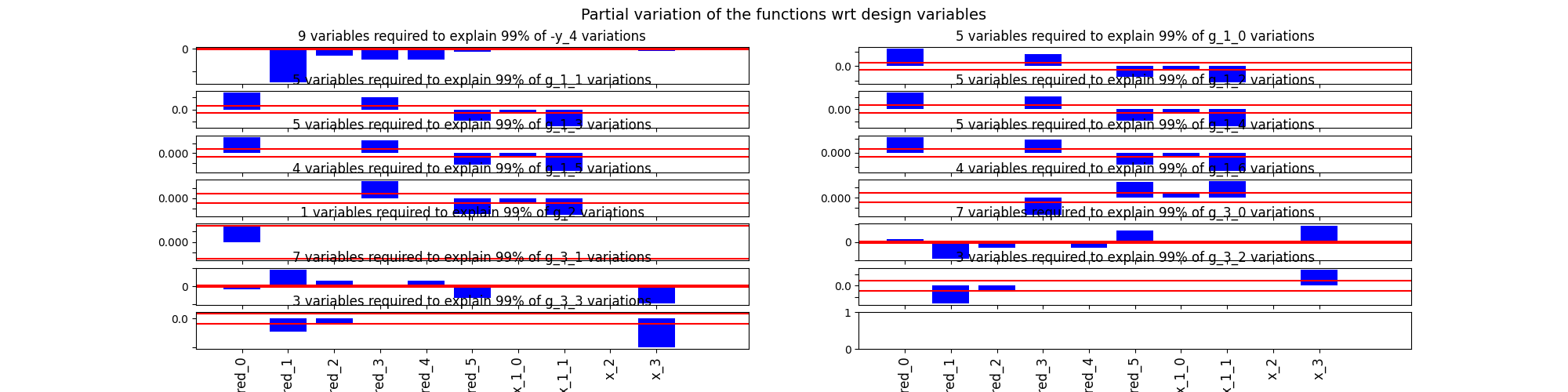
Partial variation of the functions wrt design variables, 9 variables required to explain 99% of -y_4 variations, 5 variables required to explain 99% of g_1_0 variations, 5 variables required to explain 99% of g_1_1 variations, 5 variables required to explain 99% of g_1_2 variations, 5 variables required to explain 99% of g_1_3 variations, 5 variables required to explain 99% of g_1_4 variations, 4 variables required to explain 99% of g_1_5 variations, 4 variables required to explain 99% of g_1_6 variations, 1 variables required to explain 99% of g_2 variations, 7 variables required to explain 99% of g_3_0 variations, 7 variables required to explain 99% of g_3_1 variations, 3 variables required to explain 99% of g_3_2 variations, 3 variables required to explain 99% of g_3_3 variations

    INFO - 16:55:48: VariableInfluence for function -y_4
    INFO - 16:55:48: Most influential variables indices to explain % of the function variation: 99
    INFO - 16:55:48: [1 4 3 2 5 9 7 8 0]
/home/docs/checkouts/readthedocs.org/user_builds/gemseo/envs/4.3.0.post0/lib/python3.9/site-packages/gemseo/post/variable_influence.py:230: UserWarning: FixedFormatter should only be used together with FixedLocator
  axe.set_xticklabels(x_labels, fontsize=font_size, rotation=rotation)
    INFO - 16:55:49: VariableInfluence for function g_1_0
    INFO - 16:55:49: Most influential variables indices to explain % of the function variation: 99
    INFO - 16:55:49: [0 7 3 5 6]
    INFO - 16:55:49: VariableInfluence for function g_1_1
    INFO - 16:55:49: Most influential variables indices to explain % of the function variation: 99
    INFO - 16:55:49: [7 0 3 5 6]
    INFO - 16:55:49: VariableInfluence for function g_1_2
    INFO - 16:55:49: Most influential variables indices to explain % of the function variation: 99
    INFO - 16:55:49: [7 0 3 5 6]
    INFO - 16:55:49: VariableInfluence for function g_1_3
    INFO - 16:55:49: Most influential variables indices to explain % of the function variation: 99
    INFO - 16:55:49: [7 0 3 5 6]
    INFO - 16:55:49: VariableInfluence for function g_1_4
    INFO - 16:55:49: Most influential variables indices to explain % of the function variation: 99
    INFO - 16:55:49: [7 0 3 5 6]
    INFO - 16:55:49: VariableInfluence for function g_1_5
    INFO - 16:55:49: Most influential variables indices to explain % of the function variation: 99
    INFO - 16:55:49: [3 7 5 6]
    INFO - 16:55:49: VariableInfluence for function g_1_6
    INFO - 16:55:49: Most influential variables indices to explain % of the function variation: 99
    INFO - 16:55:49: [3 7 5 6]
    INFO - 16:55:49: VariableInfluence for function g_2
    INFO - 16:55:49: Most influential variables indices to explain % of the function variation: 99
    INFO - 16:55:49: [0]
    INFO - 16:55:49: VariableInfluence for function g_3_0
    INFO - 16:55:49: Most influential variables indices to explain % of the function variation: 99
    INFO - 16:55:49: [9 1 5 2 4 0 8]
    INFO - 16:55:49: VariableInfluence for function g_3_1
    INFO - 16:55:49: Most influential variables indices to explain % of the function variation: 99
    INFO - 16:55:49: [9 1 5 2 4 0 8]
    INFO - 16:55:49: VariableInfluence for function g_3_2
    INFO - 16:55:49: Most influential variables indices to explain % of the function variation: 99
    INFO - 16:55:49: [1 9 2]
    INFO - 16:55:49: VariableInfluence for function g_3_3
    INFO - 16:55:49: Most influential variables indices to explain % of the function variation: 99
    INFO - 16:55:49: [9 1 2]

<gemseo.post.variable_influence.VariableInfluence object at 0x7fbc5562d190>

Total running time of the script: ( 0 minutes 2.366 seconds)

Download Python source code: plot_variable_influence.py

Download Jupyter notebook: plot_variable_influence.ipynb

Gallery generated by Sphinx-Gallery