Note
Go to the end to download the full example code
Morris analysis¶
from __future__ import annotations
import pprint
from gemseo.uncertainty.sensitivity.morris.analysis import MorrisAnalysis
from gemseo.uncertainty.use_cases.ishigami.ishigami_discipline import IshigamiDiscipline
from gemseo.uncertainty.use_cases.ishigami.ishigami_space import IshigamiSpace
In this example, we consider the Ishigami function [IH90]
implemented as an MDODiscipline by the IshigamiDiscipline.
It is commonly used
with the independent random variables \(X_1\), \(X_2\) and \(X_3\)
uniformly distributed between \(-\pi\) and \(\pi\)
and defined in the IshigamiSpace.
discipline = IshigamiDiscipline()
uncertain_space = IshigamiSpace()
Then,
we run sensitivity analysis of type MorrisAnalysis:
sensitivity_analysis = MorrisAnalysis([discipline], uncertain_space, 10)
sensitivity_analysis.compute_indices()
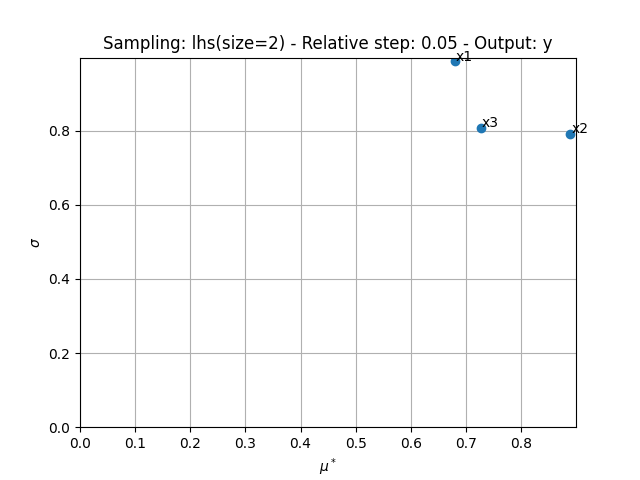
{'MU': {'y': [{'x1': array([-0.36000398]), 'x2': array([0.77781853]), 'x3': array([-0.70990541])}]}, 'MU_STAR': {'y': [{'x1': array([0.67947346]), 'x2': array([0.88906579]), 'x3': array([0.72694219])}]}, 'SIGMA': {'y': [{'x1': array([0.98724949]), 'x2': array([0.79064599]), 'x3': array([0.8074493])}]}, 'RELATIVE_SIGMA': {'y': [{'x1': array([1.45296254]), 'x2': array([0.88929976]), 'x3': array([1.11074761])}]}, 'MIN': {'y': [{'x1': array([0.0338188]), 'x2': array([0.11821721]), 'x3': array([8.72820113e-05])}]}, 'MAX': {'y': [{'x1': array([2.2360336]), 'x2': array([1.83987522]), 'x3': array([2.12052546])}]}}
The resulting indices are the empirical means and the standard deviations of the absolute output variations due to input changes.
pprint.pprint(sensitivity_analysis.indices)
{'MAX': {'y': [{'x1': array([2.2360336]),
'x2': array([1.83987522]),
'x3': array([2.12052546])}]},
'MIN': {'y': [{'x1': array([0.0338188]),
'x2': array([0.11821721]),
'x3': array([8.72820113e-05])}]},
'MU': {'y': [{'x1': array([-0.36000398]),
'x2': array([0.77781853]),
'x3': array([-0.70990541])}]},
'MU_STAR': {'y': [{'x1': array([0.67947346]),
'x2': array([0.88906579]),
'x3': array([0.72694219])}]},
'RELATIVE_SIGMA': {'y': [{'x1': array([1.45296254]),
'x2': array([0.88929976]),
'x3': array([1.11074761])}]},
'SIGMA': {'y': [{'x1': array([0.98724949]),
'x2': array([0.79064599]),
'x3': array([0.8074493])}]}}
The main indices corresponds to these empirical means
(this main method can be changed with MorrisAnalysis.main_method):
pprint.pprint(sensitivity_analysis.main_indices)
{'y': [{'x1': array([0.67947346]),
'x2': array([0.88906579]),
'x3': array([0.72694219])}]}
and can be interpreted with respect to the empirical bounds of the outputs:
pprint.pprint(sensitivity_analysis.outputs_bounds)
{'y': [array([-1.42959705]), array([14.89344259])]}
We can also sort the input parameters by decreasing order of influence:
print(sensitivity_analysis.sort_parameters("y"))
['x2', 'x3', 'x1']
Lastly,
we can use the method MorrisAnalysis.plot()
to visualize the different series of indices:
sensitivity_analysis.plot("y", save=False, show=True, lower_mu=0, lower_sigma=0)
Total running time of the script: ( 0 minutes 0.742 seconds)
