Note
Go to the end to download the full example code
IDF-based MDO on the Sobieski SSBJ test case¶
from __future__ import annotations
from gemseo import configure_logger
from gemseo import create_discipline
from gemseo import create_scenario
from gemseo import generate_n2_plot
from gemseo.problems.sobieski.core.design_space import SobieskiDesignSpace
configure_logger()
<RootLogger root (INFO)>
Instantiate the disciplines¶
First, we instantiate the four disciplines of the use case:
SobieskiPropulsion,
SobieskiAerodynamics,
SobieskiMission
and SobieskiStructure.
disciplines = create_discipline([
"SobieskiPropulsion",
"SobieskiAerodynamics",
"SobieskiMission",
"SobieskiStructure",
])
We can quickly access the most relevant information of any discipline (name, inputs,
and outputs) with Python’s print() function. Moreover, we can get the default
input values of a discipline with the attribute MDODiscipline.default_inputs
for discipline in disciplines:
print(discipline)
print(f"Default inputs: {discipline.default_inputs}")
SobieskiPropulsion
Default inputs: {'x_shared': array([5.0e-02, 4.5e+04, 1.6e+00, 5.5e+00, 5.5e+01, 1.0e+03]), 'x_3': array([0.5]), 'y_23': array([12562.01206488]), 'c_3': array([4360.])}
SobieskiAerodynamics
Default inputs: {'c_4': array([0.01375]), 'y_12': array([5.06069742e+04, 9.50000000e-01]), 'x_shared': array([5.0e-02, 4.5e+04, 1.6e+00, 5.5e+00, 5.5e+01, 1.0e+03]), 'x_2': array([1.]), 'y_32': array([0.50279625])}
SobieskiMission
Default inputs: {'y_24': array([4.15006276]), 'y_34': array([1.10754577]), 'x_shared': array([5.0e-02, 4.5e+04, 1.6e+00, 5.5e+00, 5.5e+01, 1.0e+03]), 'y_14': array([50606.9741711 , 7306.20262124])}
SobieskiStructure
Default inputs: {'c_0': array([2000.]), 'y_21': array([50606.9741711]), 'x_1': array([0.25, 1. ]), 'x_shared': array([5.0e-02, 4.5e+04, 1.6e+00, 5.5e+00, 5.5e+01, 1.0e+03]), 'y_31': array([6354.32430691]), 'c_2': array([6.]), 'c_1': array([25000.])}
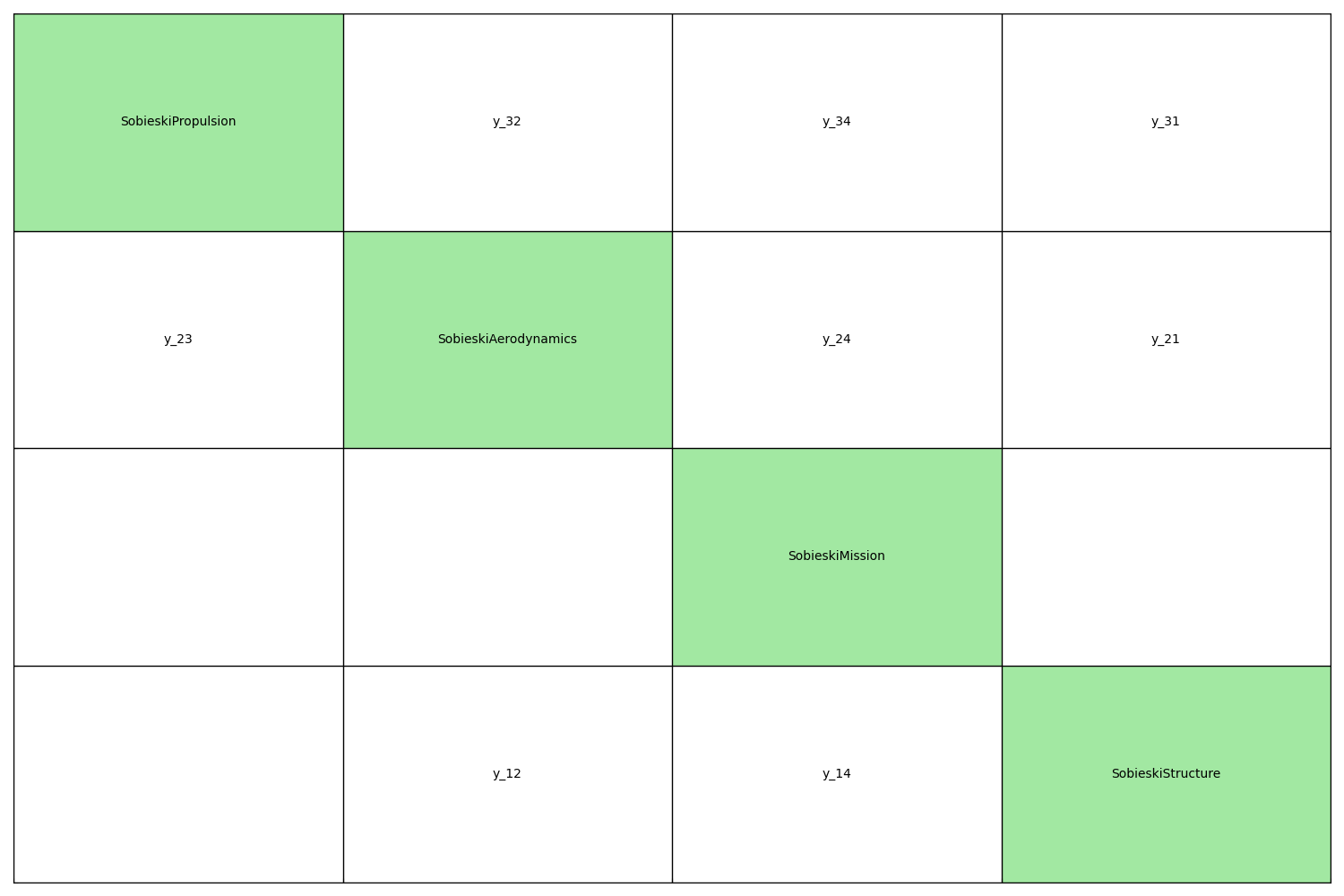
You may also be interested in plotting the couplings of your disciplines.
A quick way of getting this information is the API function
generate_n2_plot(). A much more detailed explanation of coupling
visualization is available here.
generate_n2_plot(disciplines, save=False, show=True)
Build, execute and post-process the scenario¶
Then, we build the scenario which links the disciplines
with the formulation and the optimization algorithm. Here, we use the
IDF formulation. We tell the scenario to minimize -y_4 instead of
minimizing y_4 (range), which is the default option.
Instantiate the scenario¶
design_space = SobieskiDesignSpace()
design_space
scenario = create_scenario(
disciplines,
"IDF",
"y_4",
design_space,
maximize_objective=True,
)
Set the design constraints¶
for c_name in ["g_1", "g_2", "g_3"]:
scenario.add_constraint(c_name, constraint_type="ineq")
Visualize the XDSM¶
Generate the XDSM file on the fly:
log_workflow_status=Truewill log the status of the workflow in the console,save_html(defaultTrue) will generate a self-contained HTML file, that can be automatically opened usingshow_html=True.
scenario.xdsmize(save_html=False)
Define the algorithm inputs¶
We set the maximum number of iterations, the optimizer and the optimizer options
algo_options = {
"ftol_rel": 1e-10,
"ineq_tolerance": 1e-3,
"eq_tolerance": 1e-3,
"normalize_design_space": True,
}
scn_inputs = {"max_iter": 20, "algo": "SLSQP", "algo_options": algo_options}
Execute the scenario¶
scenario.execute(scn_inputs)
INFO - 13:54:24:
INFO - 13:54:24: *** Start MDOScenario execution ***
INFO - 13:54:24: MDOScenario
INFO - 13:54:24: Disciplines: SobieskiAerodynamics SobieskiMission SobieskiPropulsion SobieskiStructure
INFO - 13:54:24: MDO formulation: IDF
INFO - 13:54:24: Optimization problem:
INFO - 13:54:24: minimize -y_4(x_shared, y_14, y_24, y_34)
INFO - 13:54:24: with respect to x_1, x_2, x_3, x_shared, y_12, y_14, y_21, y_23, y_24, y_31, y_32, y_34
INFO - 13:54:24: subject to constraints:
INFO - 13:54:24: g_1(x_shared, x_1, y_31, y_21) <= 0.0
INFO - 13:54:24: g_2(x_shared, x_2, y_32, y_12) <= 0.0
INFO - 13:54:24: g_3(x_shared, x_3, y_23) <= 0.0
INFO - 13:54:24: y_31_y_32_y_34(x_shared, x_3, y_23): y_31(x_shared, x_3, y_23) - y_31 == 0.0
INFO - 13:54:24: y_32(x_shared, x_3, y_23) - y_32 == 0.0
INFO - 13:54:24: y_34(x_shared, x_3, y_23) - y_34 == 0.0
INFO - 13:54:24: y_21_y_23_y_24(x_shared, x_2, y_32, y_12): y_21(x_shared, x_2, y_32, y_12) - y_21 == 0.0
INFO - 13:54:24: y_23(x_shared, x_2, y_32, y_12) - y_23 == 0.0
INFO - 13:54:24: y_24(x_shared, x_2, y_32, y_12) - y_24 == 0.0
INFO - 13:54:24: y_12_y_14(x_shared, x_1, y_31, y_21): y_12(x_shared, x_1, y_31, y_21) - y_12 == 0.0
INFO - 13:54:24: y_14(x_shared, x_1, y_31, y_21) - y_14 == 0.0
INFO - 13:54:24: over the design space:
INFO - 13:54:24: +-------------+-------------+--------------------+-------------+-------+
INFO - 13:54:24: | Name | Lower bound | Value | Upper bound | Type |
INFO - 13:54:24: +-------------+-------------+--------------------+-------------+-------+
INFO - 13:54:24: | x_shared[0] | 0.01 | 0.05 | 0.09 | float |
INFO - 13:54:24: | x_shared[1] | 30000 | 45000 | 60000 | float |
INFO - 13:54:24: | x_shared[2] | 1.4 | 1.6 | 1.8 | float |
INFO - 13:54:24: | x_shared[3] | 2.5 | 5.5 | 8.5 | float |
INFO - 13:54:24: | x_shared[4] | 40 | 55 | 70 | float |
INFO - 13:54:24: | x_shared[5] | 500 | 1000 | 1500 | float |
INFO - 13:54:24: | x_1[0] | 0.1 | 0.25 | 0.4 | float |
INFO - 13:54:24: | x_1[1] | 0.75 | 1 | 1.25 | float |
INFO - 13:54:24: | x_2 | 0.75 | 1 | 1.25 | float |
INFO - 13:54:24: | x_3 | 0.1 | 0.5 | 1 | float |
INFO - 13:54:24: | y_14[0] | 24850 | 50606.9741711 | 77100 | float |
INFO - 13:54:24: | y_14[1] | -7700 | 7306.20262124 | 45000 | float |
INFO - 13:54:24: | y_32 | 0.235 | 0.5027962499999999 | 0.795 | float |
INFO - 13:54:24: | y_31 | 2960 | 6354.32430691 | 10185 | float |
INFO - 13:54:24: | y_24 | 0.44 | 4.15006276 | 11.13 | float |
INFO - 13:54:24: | y_34 | 0.44 | 1.10754577 | 1.98 | float |
INFO - 13:54:24: | y_23 | 3365 | 12194.2671934 | 26400 | float |
INFO - 13:54:24: | y_21 | 24850 | 50606.9741711 | 77250 | float |
INFO - 13:54:24: | y_12[0] | 24850 | 50606.9742 | 77250 | float |
INFO - 13:54:24: | y_12[1] | 0.45 | 0.95 | 1.5 | float |
INFO - 13:54:24: +-------------+-------------+--------------------+-------------+-------+
INFO - 13:54:24: Solving optimization problem with algorithm SLSQP:
INFO - 13:54:24: 5%|▌ | 1/20 [00:00<00:00, 252.79 it/sec, obj=-536]
INFO - 13:54:24: 10%|█ | 2/20 [00:00<00:00, 59.17 it/sec, obj=-1.49e+3]
INFO - 13:54:24: 15%|█▌ | 3/20 [00:00<00:00, 61.64 it/sec, obj=-3.83e+3]
INFO - 13:54:24: 20%|██ | 4/20 [00:00<00:00, 62.86 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 25%|██▌ | 5/20 [00:00<00:00, 63.61 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 30%|███ | 6/20 [00:00<00:00, 64.26 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 35%|███▌ | 7/20 [00:00<00:00, 64.54 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 40%|████ | 8/20 [00:00<00:00, 64.92 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 45%|████▌ | 9/20 [00:00<00:00, 69.15 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 50%|█████ | 10/20 [00:00<00:00, 68.97 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 55%|█████▌ | 11/20 [00:00<00:00, 72.40 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 60%|██████ | 12/20 [00:00<00:00, 75.46 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 65%|██████▌ | 13/20 [00:00<00:00, 78.31 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 70%|███████ | 14/20 [00:00<00:00, 80.98 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 75%|███████▌ | 15/20 [00:00<00:00, 83.47 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 80%|████████ | 16/20 [00:00<00:00, 85.80 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 85%|████████▌ | 17/20 [00:00<00:00, 87.96 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 90%|█████████ | 18/20 [00:00<00:00, 89.97 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 95%|█████████▌| 19/20 [00:00<00:00, 91.84 it/sec, obj=-3.96e+3]
INFO - 13:54:24: 100%|██████████| 20/20 [00:00<00:00, 93.60 it/sec, obj=-3.96e+3]
INFO - 13:54:24: Optimization result:
INFO - 13:54:24: Optimizer info:
INFO - 13:54:24: Status: 8
INFO - 13:54:24: Message: Positive directional derivative for linesearch
INFO - 13:54:24: Number of calls to the objective function by the optimizer: 21
INFO - 13:54:24: Solution:
INFO - 13:54:24: The solution is feasible.
INFO - 13:54:24: Objective: -3963.909125280606
INFO - 13:54:24: Standardized constraints:
INFO - 13:54:24: g_1 = [-0.01807265 -0.03335477 -0.04425595 -0.0518399 -0.05733055 -0.13720865
INFO - 13:54:24: -0.10279135]
INFO - 13:54:24: g_2 = 7.162693463458325e-06
INFO - 13:54:24: g_3 = [-7.67188159e-01 -2.32811841e-01 -3.73860557e-05 -1.83255000e-01]
INFO - 13:54:24: y_12_y_14 = [ 1.12943503e-05 4.28787041e-07 1.13267743e-05 -1.50426345e-05]
INFO - 13:54:24: y_21_y_23_y_24 = [-2.77708306e-16 1.33085464e-05 -2.62473913e-05]
INFO - 13:54:24: y_31_y_32_y_34 = [-2.35661889e-06 -2.32437808e-06 1.57269783e-05]
INFO - 13:54:24: Design space:
INFO - 13:54:24: +-------------+-------------+---------------------+-------------+-------+
INFO - 13:54:24: | Name | Lower bound | Value | Upper bound | Type |
INFO - 13:54:24: +-------------+-------------+---------------------+-------------+-------+
INFO - 13:54:24: | x_shared[0] | 0.01 | 0.06000179067336589 | 0.09 | float |
INFO - 13:54:24: | x_shared[1] | 30000 | 60000 | 60000 | float |
INFO - 13:54:24: | x_shared[2] | 1.4 | 1.4 | 1.8 | float |
INFO - 13:54:24: | x_shared[3] | 2.5 | 2.5 | 8.5 | float |
INFO - 13:54:24: | x_shared[4] | 40 | 70 | 70 | float |
INFO - 13:54:24: | x_shared[5] | 500 | 1500 | 1500 | float |
INFO - 13:54:24: | x_1[0] | 0.1 | 0.4 | 0.4 | float |
INFO - 13:54:24: | x_1[1] | 0.75 | 0.75 | 1.25 | float |
INFO - 13:54:24: | x_2 | 0.75 | 0.75 | 1.25 | float |
INFO - 13:54:24: | x_3 | 0.1 | 0.156238904271528 | 1 | float |
INFO - 13:54:24: | y_14[0] | 24850 | 44749.85202975167 | 77100 | float |
INFO - 13:54:24: | y_14[1] | -7700 | 19351.86291108692 | 45000 | float |
INFO - 13:54:24: | y_32 | 0.235 | 0.7328131425977524 | 0.795 | float |
INFO - 13:54:24: | y_31 | 2960 | 9437.362336215188 | 10185 | float |
INFO - 13:54:24: | y_24 | 0.44 | 8.05763183450019 | 11.13 | float |
INFO - 13:54:24: | y_34 | 0.44 | 0.9239115967364436 | 1.98 | float |
INFO - 13:54:24: | y_23 | 3365 | 5553.60943830111 | 26400 | float |
INFO - 13:54:24: | y_21 | 24850 | 44749.85202975168 | 77250 | float |
INFO - 13:54:24: | y_12[0] | 24850 | 44749.85202975167 | 77250 | float |
INFO - 13:54:24: | y_12[1] | 0.45 | 0.9027908995968825 | 1.5 | float |
INFO - 13:54:24: +-------------+-------------+---------------------+-------------+-------+
INFO - 13:54:24: *** End MDOScenario execution (time: 0:00:00.256024) ***
{'max_iter': 20, 'algo_options': {'ftol_rel': 1e-10, 'ineq_tolerance': 0.001, 'eq_tolerance': 0.001, 'normalize_design_space': True}, 'algo': 'SLSQP'}
Save the optimization history¶
We can save the whole optimization problem and its history for further post processing:
scenario.save_optimization_history("idf_history.h5", file_format="hdf5")
INFO - 13:54:24: Exporting the optimization problem to the file idf_history.h5 at node
We can also save only calls to functions and design variables history:
scenario.save_optimization_history("idf_history.xml", file_format="ggobi")
Print optimization metrics¶
scenario.print_execution_metrics()
INFO - 13:54:24: Scenario Execution Statistics
INFO - 13:54:24: Discipline: SobieskiPropulsion
INFO - 13:54:24: Executions number: 20
INFO - 13:54:24: Execution time: 0.010818926049978472 s
INFO - 13:54:24: Linearizations number: 9
INFO - 13:54:24: Discipline: SobieskiAerodynamics
INFO - 13:54:24: Executions number: 20
INFO - 13:54:24: Execution time: 0.014511272951494902 s
INFO - 13:54:24: Linearizations number: 9
INFO - 13:54:24: Discipline: SobieskiMission
INFO - 13:54:24: Executions number: 20
INFO - 13:54:24: Execution time: 0.0010142520477529615 s
INFO - 13:54:24: Linearizations number: 9
INFO - 13:54:24: Discipline: SobieskiStructure
INFO - 13:54:24: Executions number: 20
INFO - 13:54:24: Execution time: 0.07281165002495982 s
INFO - 13:54:24: Linearizations number: 9
INFO - 13:54:24: Total number of executions calls: 80
INFO - 13:54:24: Total number of linearizations: 36
Plot the optimization history view¶
scenario.post_process("OptHistoryView", save=True, show=True)
<gemseo.post.opt_history_view.OptHistoryView object at 0x7f2d18e3fe50>
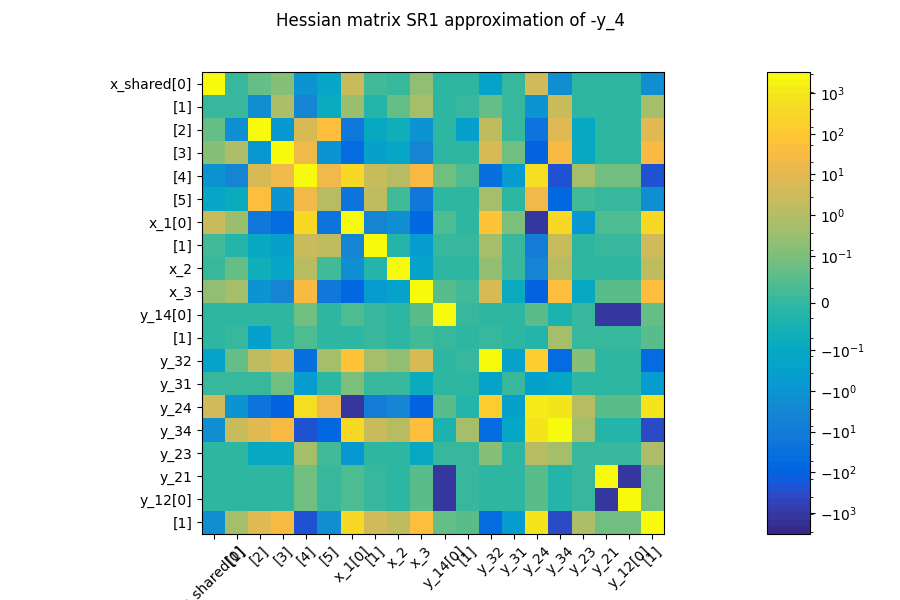
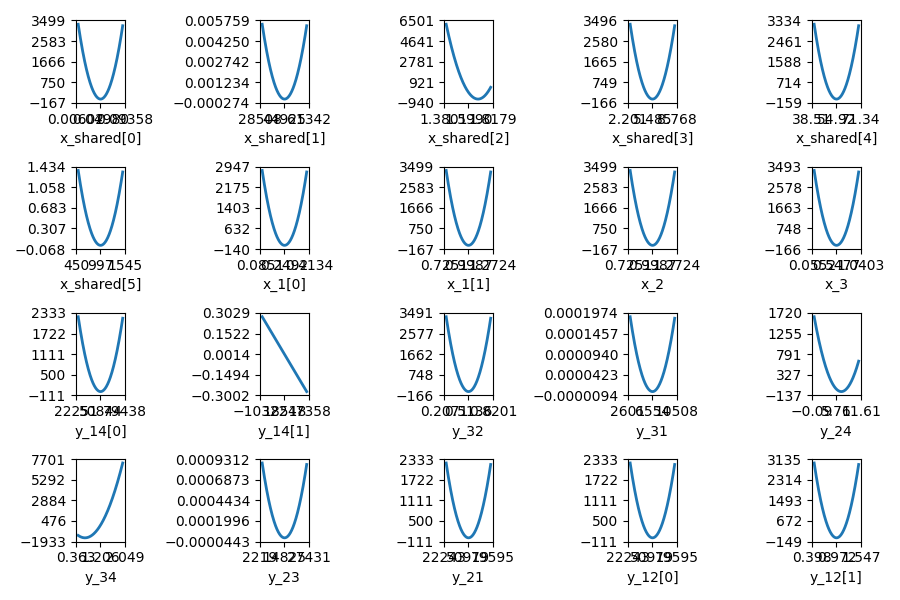
Plot the quadratic approximation of the objective¶
scenario.post_process("QuadApprox", function="-y_4", save=False, show=True)
<gemseo.post.quad_approx.QuadApprox object at 0x7f2d189992e0>
Total running time of the script: (0 minutes 4.747 seconds)