problem module¶
The Sobieski’s SSBJ problem.
- class gemseo.problems.sobieski.core.problem.SobieskiProblem(dtype='float64')[source]
Bases:
objectThe Sobieski’s SSBJ problem.
This problem seeks to maximize the range of a supersonic business jet (SSBJ) over a bounded design space whilst satisfying inequality constraints.
The objective and constraint functions come from a system of four disciplines:
the structure, computing the total aircraft mass \(y_{1,4,0}\) and \(y_{1,2,0}\), the fuel mass \(y_{1,4,1}\), the wing twist \(y_{1,2,1}\) and the five stress constraints \(g_{1,0},\ldots,g_{4,0}\).
the aerodynamics discipline, computing the lift \(y_{2,1}\), drag \(y_{2,3}\), lift-to-drag ratio and pressure gradient constraint \(g_2\),
the propulsion, computing the engine mass \(y_{3,1,0}\), the engine scale factor \(y_{3,2,0}\), which is also the constraint \(g_{3,0}\), the specific fuel consumption \(y_{3,4,0}\), the engine temperature constraint \(g_{3,1}\), and the throttle setting constraint \(g_{3,2}\)
the mission, computing the range \(y_{4,0}\).
Notes
The structure, aerodynamics, propulsion and mission disciplines are numbered from 1 to 4.
The variable \(y_{i,j,k}\) is a coupling variable from the discipline \(i\) to the discipline \(j\).
The aerodynamics, structure and propulsion disciplines are strongly coupled, i.e. each of them depends directly or indirectly on the others, and provide inputs to the mission discipline.
The design variables can be classified into four groups:
the design variables which are inputs to at least two disciplines,
\(x_{0,0}\): the thickness-to-chord ratio,
\(x_{0,1}\): the altitude (ft),
\(x_{0,2}\): the Mach number,
\(x_{0,3}\): the aspect ratio,
\(x_{0,4}\): the wing sweep (deg),
\(x_{0,5}\): the wing surface area (ft 2),
the design variables which are inputs of the structure discipline only:
\(x_{1,0}\): the wing taper ratio,
\(x_{1,1}\): the wingbox x-sectional area
the design variables which are inputs of the aerodynamics discipline only:
\(x_{2,0}\): the skin friction coefficient,
the design variables which are inputs of the propulsion discipline only:
\(x_{3,0}\): the throttle setting (engin mass flow).
Lastly, this problem is based on five constants:
\(c_0\): the minimum fuel weight,
\(c_1\): the miscellaneous weight,
\(c_2\): the maximum load factor,
\(c_3\): the reference engine weight,
\(c_4\): the minimum drag coefficient.
- Parameters:
dtype (str) –
The data type for the NumPy arrays, either “float64” or “complex128”.
By default it is set to “float64”.
- get_bounds_by_name(variable_names)[source]
Return the lower and upper bounds of variables.
- get_constraints(design_vector, true_cstr=False)[source]
Compute all the constraints.
- Parameters:
- Returns:
The value of the constraints \(g_1\), \(g_2\) and \(g_3\).
- Return type:
- get_default_inputs(names=None)[source]
Return the default variable values at the default initial point.
- get_default_inputs_equilibrium(names=None)[source]
Return the default variable values at a multidisciplinary feasible point.
The coupling variables are at the equilibrium, in the sense of the multidisciplinary analysis (MDA).
- get_default_inputs_feasible(names=None)[source]
Return the default variable values at the default initial feasible point.
- get_random_input(names=None, seed=None)[source]
Return a randomized starting point related to some input variables.
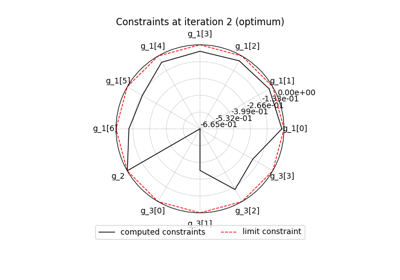
- get_sobieski_constraints(g_1, g_2, g_3, true_cstr=False)[source]
Return either the value of the constraints or the distance to the thresholds.
- Parameters:
g_1 (ndarray) – The constraints from the structure discipline:
g_1[0]tog_1[4]are the stresses on wing andg_1[5]is the wing twist.g_2 (ndarray) – The constraint (pressure gradient) from the aerodynamics discipline.
g_3 (ndarray) –
The constraints from the propulsion discipline:
g_3[0]is the engine scale factor,g_3[1]is the engine temperature andg_3[2]is the throttle setting constraint.true_cstr (ndarray) –
If
True, return the value of the outputs. Otherwise, return the distance to the corresponding constraint thresholds.By default it is set to False.
- Returns:
The constraints or the distance to the thresholds, according to
true_cstr.- Return type:
- get_x0_feasible(names=None)[source]
Return a feasible starting point related to some input variables.
- normalize_inputs(input_vector)[source]
Normalize an input vector with respect to the variable bounds.
- unnormalize_inputs(input_vector)[source]
Unnormalize an input vector with respect to the variable bounds.
- CONTRAINTS_NAMES = ('Stress_x1', 'Stress_x2', 'Stress_x3', 'Stress_x4', 'Stress_x5', 'Twist', 'Pgrad', 'ESF', 'Temperature', 'Throttle')
- CONTRAINTS_NAMES_INEQUALITY = ('c_Stress_x1', 'c_Stress_x2', 'c_Stress_x3', 'c_Stress_x4', 'c_Stress_x5', 'c_Twist_upper', 'c_Twist_lower', 'c_Pgrad', 'c_ESF_upper', 'c_ESF_lower', 'c_Throttle', 'c_Temperature')
- COUPLING_VARIABLES_NAMES = ('Total weight', 'Fuel weight', 'Wing twist', 'Lift', 'Drag', 'Lift/Drag', 'SFC', 'Engine weight')
- DV_NAMES = ('TaperRatio', 'SectionalArea', 'Cf', 'Throttle_setting', 'eta', 'h', 'Mach', 'AR', 'Phi', 'sref')
- DV_NAMES_NORMALIZED = ('x_TaperRatio', 'x_SectionalArea', 'x_Cf', 'x_Throttle_setting', 'x_eta', 'x_h', 'x_Mach', 'x_AR', 'x_Phi', 'x_sref')
- ESF_LOWER_LIMIT = 0.5
- ESF_UPPER_LIMIT = 1.5
- PRESSURE_GRADIENT_LIMIT = 1.04
- STRESS_LIMIT = 1.09
- TEMPERATURE_LIMIT = 1.02
- TWIST_LOWER_LIMIT = 0.8
- TWIST_UPPER_LIMIT = 1.04
- USE_ORIGINAL_DESIGN_VARIABLES_ORDER: ClassVar[bool] = False
Whether to sort the
DesignSpaceas in [SSAJr98].If so, the order of the design variables will be
"x_1","x_2","x_3"and"x_shared". Otherwise,"x_shared","x_1","x_2"and"x_3".
- property aerodynamics: SobieskiAerodynamics
The aerodynamics discipline.
- property constants: ndarray
The constant vector.
- property design_bounds: tuple[numpy.ndarray, numpy.ndarray]
The lower and upper bounds of the design variables.
- property design_space: DesignSpace
The design space.
- property design_space_with_physical_naming: DesignSpace
The design space with physical naming.
- property initial_design: ndarray
The initial design \(x\).
- property mission: SobieskiMission
The mission discipline.
- property optimum_design: ndarray
The optimal design vector found by Sobieski with BLISS.
- property optimum_range: ndarray
The optimal range found by Sobieski with BLISS.
- property propulsion: SobieskiPropulsion
The propulsion discipline.
- property structure: SobieskiStructure
The structure discipline.
Examples using SobieskiProblem¶
Application: Sobieski’s Super-Sonic Business Jet (MDO)
Simple disciplinary DOE example on the Sobieski SSBJ test case

Example for exterior penalty applied to the Sobieski test case.