mdo_scenario module¶
A scenario whose driver is an optimization algorithm.
- class gemseo.core.mdo_scenario.MDOScenario(disciplines, formulation, objective_name, design_space, name=None, grammar_type=GrammarType.JSON, maximize_objective=False, **formulation_options)[source]
Bases:
ScenarioA multidisciplinary scenario to be executed by an optimizer.
an
MDOScenariois a particularScenariowhose driver is an optimization algorithm. This algorithm must be implemented in anOptimizationLibrary.Initialize self. See help(type(self)) for accurate signature.
- Parameters:
disciplines (Sequence[MDODiscipline]) – The disciplines used to compute the objective, constraints and observables from the design variables.
formulation (str) – The class name of the
MDOFormulation, e.g."MDF","IDF"or"BiLevel".objective_name (str | Sequence[str]) – The name(s) of the discipline output(s) used as objective. If multiple names are passed, the objective will be a vector.
design_space (DesignSpace) – The search space including at least the design variables (some formulations requires additional variables, e.g.
IDFwith the coupling variables).name (str | None) – The name to be given to this scenario. If
None, use the name of the class.grammar_type (MDODiscipline.GrammarType) –
The type of the input and output grammars.
By default it is set to “JSONGrammar”.
maximize_objective (bool) –
Whether to maximize the objective.
By default it is set to False.
**formulation_options (Any) – The options of the
MDOFormulation.
- MAX_ITER = 'max_iter'
- X_OPT = 'x_opt'
- cache: AbstractCache | None
The cache containing one or several executions of the discipline according to the cache policy.
- clear_history_before_run: bool
If
True, clear history before run.
- data_processor: DataProcessor
A tool to pre- and post-process discipline data.
- exec_for_lin: bool
Whether the last execution was due to a linearization.
- formulation: MDOFormulation
The MDO formulation.
- formulation_name: str
The name of the MDO formulation.
- input_grammar: BaseGrammar
The input grammar.
- jac: dict[str, dict[str, ndarray]]
The Jacobians of the outputs wrt inputs.
The structure is
{output: {input: matrix}}.
- name: str
The name of the discipline.
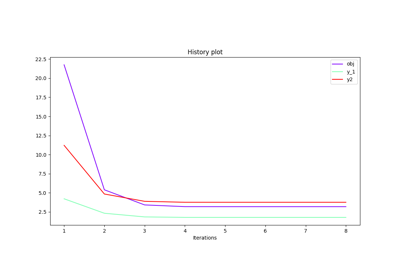
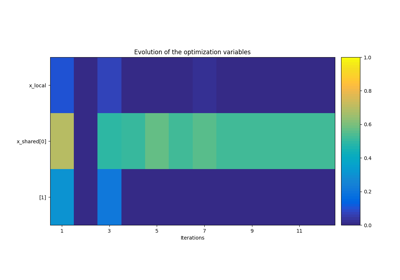
- optimization_result: OptimizationResult
The optimization result.
- output_grammar: BaseGrammar
The output grammar.
- re_exec_policy: ReExecutionPolicy
The policy to re-execute the same discipline.
- residual_variables: Mapping[str, str]
The output variables mapping to their inputs, to be considered as residuals; they shall be equal to zero.
- run_solves_residuals: bool
Whether the run method shall solve the residuals.
Examples using MDOScenario¶
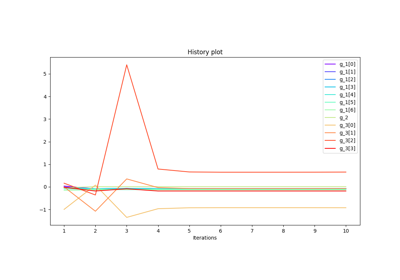
Example for exterior penalty applied to the Sobieski test case.
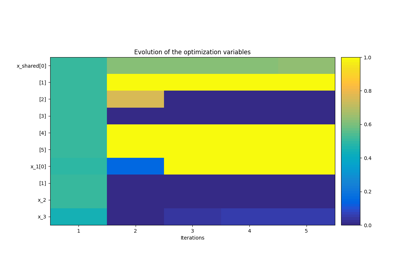
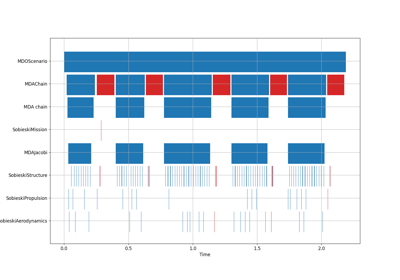
Application: Sobieski’s Super-Sonic Business Jet (MDO)

MDO formulations for a toy example in aerostructure

Solve a 2D short cantilever topology optimization problem
Pareto front on Binh and Korn problem using a BiLevel formulation