rbf module¶

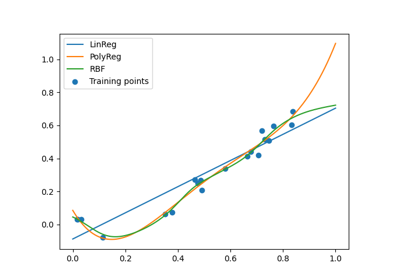
The RBF network for regression.

The radial basis function surrogate discipline expresses the model output as a weighted sum of kernel functions centered on the learning input data:

\[y = w_1K(\|x-x_1\|;\epsilon) + w_2K(\|x-x_2\|;\epsilon) + \ldots + w_nK(\|x-x_n\|;\epsilon)\]

and the coefficients \((w_1, w_2, \ldots, w_n)\) are estimated by least squares minimization.

Dependence¶

The RBF model relies on the Rbf class of the scipy library.

class gemseo.mlearning.regression.rbf.RBFRegressor(data, transformer=mappingproxy({}), input_names=None, output_names=None, function=Function.MULTIQUADRIC, der_function=None, epsilon=None, smooth=0.0, norm='euclidean')[source]¶

Bases: MLRegressionAlgo

Regression based on radial basis functions (RBFs).

This model relies on the SciPy class scipy.interpolate.Rbf.

Parameters:

data (IODataset) – The learning dataset.
transformer (TransformerType) –
The strategies to transform the variables. The values are instances of Transformer while the keys are the names of either the variables or the groups of variables, e.g. "inputs" or "outputs" in the case of the regression algorithms. If a group is specified, the Transformer will be applied to all the variables of this group. If IDENTITY, do not transform the variables.

By default it is set to {}.
input_names (Iterable[str] | None) – The names of the input variables. If None, consider all the input variables of the learning dataset.
output_names (Iterable[str] | None) – The names of the output variables. If None, consider all the output variables of the learning dataset.
function (Function | Callable[[float, float], float]) –
The radial basis function taking a radius \(r\) as input, representing a distance between two points. If it is a string, then it must be one of the following:
- "multiquadric" for \(\sqrt{(r/\epsilon)^2 + 1}\),
- "inverse" for \(1/\sqrt{(r/\epsilon)^2 + 1}\),
- "gaussian" for \(\exp(-(r/\epsilon)^2)\),
- "linear" for \(r\),
- "cubic" for \(r^3\),
- "quintic" for \(r^5\),
- "thin_plate" for \(r^2\log(r)\).
If it is a callable, then it must take the two arguments self and r as inputs, e.g. lambda self, r: sqrt((r/self.epsilon)**2 + 1) for the multiquadric function. The epsilon parameter will be available as self.epsilon. Other keyword arguments passed in will be available as well.

By default it is set to “multiquadric”.
der_function (Callable[[ndarray], ndarray] | None) – The derivative of the radial basis function, only to be provided if function is a callable and if the use of the model with its derivative is required. If None and if function is a callable, an error will be raised. If None and if function is a string, the class will look for its internal implementation and will raise an error if it is missing. The der_function shall take three arguments (input_data, norm_input_data, eps). For an RBF of the form function(\(r\)), der_function(\(x\), \(|x|\), \(\epsilon\)) shall return \(\epsilon^{-1} x/|x| f'(|x|/\epsilon)\).
epsilon (float | None) – An adjustable constant for Gaussian or multiquadric functions. If None, use the average distance between input data.
smooth (float) –
The degree of smoothness, 0 involving an interpolation of the learning points.

By default it is set to 0.0.
norm (str | Callable[[ndarray, ndarray], float]) –
The distance metric to be used, either a distance function name known by SciPy or a function that computes the distance between two points.

By default it is set to “euclidean”.

Raises:

ValueError – When both the variable and the group it belongs to have a transformer.

class DataFormatters¶

Bases: DataFormatters

Machine learning regression model decorators.

classmethod format_dict(predict)¶

Make an array-based function be called with a dictionary of NumPy arrays.

Parameters:: predict (Callable[[ndarray], ndarray]) – The function to be called; it takes a NumPy array in input and returns a NumPy array.
Returns:: A function making the function ‘predict’ work with either a NumPy data array or a dictionary of NumPy data arrays indexed by variables names. The evaluation will have the same type as the input data.
Return type:: Callable[[ndarray | Mapping[str, ndarray]], ndarray | Mapping[str, ndarray]]

classmethod format_dict_jacobian(predict_jac)¶

Wrap an array-based function to make it callable with a dictionary of NumPy arrays.

Parameters:: predict_jac (Callable[[ndarray], ndarray]) – The function to be called; it takes a NumPy array in input and returns a NumPy array.
Returns:: The wrapped ‘predict_jac’ function, callable with either a NumPy data array or a dictionary of numpy data arrays indexed by variables names. The return value will have the same type as the input data.
Return type:: Callable[[ndarray | Mapping[str, ndarray]], ndarray | Mapping[str, ndarray]]

classmethod format_input_output(predict)¶

Make a function robust to type, array shape and data transformation.

Parameters:: predict (Callable[[ndarray], ndarray]) – The function of interest to be called.
Returns:: A function calling the function of interest ‘predict’, while guaranteeing consistency in terms of data type and array shape, and applying input and/or output data transformation if required.
Return type:: Callable[[ndarray | Mapping[str, ndarray]], ndarray | Mapping[str, ndarray]]

classmethod format_samples(predict)¶

Make a 2D NumPy array-based function work with 1D NumPy array.

Parameters:: predict (Callable[[ndarray], ndarray]) – The function to be called; it takes a 2D NumPy array in input and returns a 2D NumPy array. The first dimension represents the samples while the second one represents the components of the variables.
Returns:: A function making the function ‘predict’ work with either a 1D NumPy array or a 2D NumPy array. The evaluation will have the same dimension as the input data.
Return type:: Callable[[ndarray], ndarray]

classmethod format_transform(transform_inputs=True, transform_outputs=True)¶

Force a function to transform its input and/or output variables.

Parameters:

transform_inputs (bool) –
Whether to transform the input variables.

By default it is set to True.
transform_outputs (bool) –
Whether to transform the output variables.

By default it is set to True.

Returns:

A function evaluating a function of interest, after transforming its input data and/or before transforming its output data.

Return type:

Callable[[ndarray], ndarray]

classmethod transform_jacobian(predict_jac)¶

Apply transformation to inputs and inverse transformation to outputs.

Parameters:: predict_jac (Callable[[ndarray], ndarray]) – The function of interest to be called.
Returns:: A function evaluating the function ‘predict_jac’, after transforming its input data and/or before transforming its output data.
Return type:: Callable[[ndarray], ndarray]

class Function(value)[source]¶

Bases: StrEnum

The radial basis functions.

CUBIC = 'cubic'¶

GAUSSIAN = 'gaussian'¶

INVERSE_MULTIQUADRIC = 'inverse_multiquadric'¶

LINEAR = 'linear'¶

MULTIQUADRIC = 'multiquadric'¶

QUINTIC = 'quintic'¶

THIN_PLATE = 'thin_plate'¶

class RBFDerivatives[source]¶

Bases: object

Derivatives of functions used in RBFRegressor.

For an RBF of the form \(f(r)\), \(r\) scalar, the derivative functions are defined by \(d(f(r))/dx\), with \(r=|x|/\epsilon\). The functions are thus defined by \(df/dx = \epsilon^{-1} x/|x| f'(|x|/\epsilon)\). This convention is chosen to avoid division by \(|x|\) when the terms may be cancelled out, as \(f'(r)\) often has a term in \(r\).

classmethod der_cubic(input_data, norm_input_data, eps)[source]¶

Compute derivative w.r.t. \(x\) of the function \(f(r) = r^3\).

Parameters:

input_data (ndarray) – The 1D input data.
norm_input_data (float) – The norm of the input variable.
eps (float) – The correlation length.

Returns:

The derivative of the function.

Return type:

ndarray

classmethod der_gaussian(input_data, norm_input_data, eps)[source]¶

Compute derivative w.r.t. \(x\) of the function \(f(r) = \exp(-r^2)\).

Parameters:

input_data (ndarray) – The 1D input data.
norm_input_data (float) – The norm of the input variable.
eps (float) – The correlation length.

Returns:

The derivative of the function.

Return type:

ndarray

classmethod der_inverse_multiquadric(input_data, norm_input_data, eps)[source]¶

Compute derivative w.r.t. \(x\) of the function \(f(r) = 1/\sqrt{r^2 + 1}\).

Parameters:

input_data (ndarray) – The 1D input data.
norm_input_data (float) – The norm of the input variable.
eps (float) – The correlation length.

Returns:

The derivative of the function.

Return type:

ndarray

classmethod der_linear(input_data, norm_input_data, eps)[source]¶

Compute derivative w.r.t. \(x\) of the function \(f(r) = r\). If \(x=0\), return 0 (determined up to a tolerance).

Parameters:

input_data (ndarray) – The 1D input data.
norm_input_data (float) – The norm of the input variable.
eps (float) – The correlation length.

Returns:

The derivative of the function.

Return type:

ndarray

classmethod der_multiquadric(input_data, norm_input_data, eps)[source]¶

Compute derivative of \(f(r) = \sqrt{r^2 + 1}\) wrt \(x\).

Parameters:

input_data (ndarray) – The 1D input data.
norm_input_data (float) – The norm of the input variable.
eps (float) – The correlation length.

Returns:

The derivative of the function.

Return type:

ndarray

classmethod der_quintic(input_data, norm_input_data, eps)[source]¶

Compute derivative w.r.t. \(x\) of the function \(f(r) = r^5\).

Parameters:

input_data (ndarray) – The 1D input data.
norm_input_data (float) – The norm of the input variable.
eps (float) – The correlation length.

Returns:

The derivative of the function.

Return type:

ndarray

classmethod der_thin_plate(input_data, norm_input_data, eps)[source]¶

Compute derivative w.r.t. \(x\) of the function \(f(r) = r^2 \log(r)\). If \(x=0\), return 0 (determined up to a tolerance).

Parameters:

input_data (ndarray) – The 1D input data.
norm_input_data (float) – The norm of the input variable.
eps (float) – The correlation length.

Returns:

The derivative of the function.

Return type:

ndarray

TOL = 2.220446049250313e-16¶

learn(samples=None, fit_transformers=True)¶

Train the machine learning algorithm from the learning dataset.

Parameters:

samples (Sequence[int] | None) – The indices of the learning samples. If None, use the whole learning dataset.
fit_transformers (bool) –
Whether to fit the variable transformers.

By default it is set to True.

Return type:

None

load_algo(directory)¶

Load a machine learning algorithm from a directory.

Parameters:: directory (str | Path) – The path to the directory where the machine learning algorithm is saved.
Return type:: None

predict(input_data, *args, **kwargs)¶

Evaluate ‘predict’ with either array or dictionary-based input data.

Firstly, the pre-processing stage converts the input data to a NumPy data array, if these data are expressed as a dictionary of NumPy data arrays.

Then, the processing evaluates the function ‘predict’ from this NumPy input data array.

Lastly, the post-processing transforms the output data to a dictionary of output NumPy data array if the input data were passed as a dictionary of NumPy data arrays.

Parameters:

input_data (ndarray | Mapping[str, ndarray]) – The input data.
*args – The positional arguments of the function ‘predict’.
**kwargs – The keyword arguments of the function ‘predict’.

Returns:

The output data with the same type as the input one.

Return type:

ndarray | Mapping[str, ndarray]

predict_jacobian(input_data, *args, **kwargs)¶

Evaluate ‘predict_jac’ with either array or dictionary-based data.

Firstly, the pre-processing stage converts the input data to a NumPy data array, if these data are expressed as a dictionary of NumPy data arrays.

Then, the processing evaluates the function ‘predict_jac’ from this NumPy input data array.

Lastly, the post-processing transforms the output data to a dictionary of output NumPy data array if the input data were passed as a dictionary of NumPy data arrays.

Parameters:

input_data – The input data.
*args – The positional arguments of the function ‘predict_jac’.
**kwargs – The keyword arguments of the function ‘predict_jac’.

Returns:

The output data with the same type as the input one.

predict_raw(input_data)¶

Predict output data from input data.

Parameters:: input_data (ndarray) – The input data with shape (n_samples, n_inputs).
Returns:: The predicted output data with shape (n_samples, n_outputs).
Return type:: ndarray

to_pickle(directory=None, path='.', save_learning_set=False)¶

Save the machine learning algorithm.

Parameters:

directory (str | None) – The name of the directory to save the algorithm.
path (str | Path) –
The path to parent directory where to create the directory.

By default it is set to “.”.
save_learning_set (bool) –
Whether to save the learning set or get rid of it to lighten the saved files.

By default it is set to False.

Returns:

The path to the directory where the algorithm is saved.

Return type:

str

DEFAULT_TRANSFORMER: DefaultTransformerType = mappingproxy({'inputs': <gemseo.mlearning.transformers.scaler.min_max_scaler.MinMaxScaler object>, 'outputs': <gemseo.mlearning.transformers.scaler.min_max_scaler.MinMaxScaler object>})¶: The default transformer for the input and output data, if any.

EUCLIDEAN: Final[str] = 'euclidean'¶

FILENAME: ClassVar[str] = 'ml_algo.pkl'¶

IDENTITY: Final[DefaultTransformerType] = mappingproxy({})¶: A transformer leaving the input and output variables as they are.

LIBRARY: Final[str] = 'SciPy'¶: The name of the library of the wrapped machine learning algorithm.

SHORT_ALGO_NAME: ClassVar[str] = 'RBF'¶

The short name of the machine learning algorithm, often an acronym.

Typically used for composite names, e.g. f"{algo.SHORT_ALGO_NAME}_{dataset.name}" or f"{algo.SHORT_ALGO_NAME}_{discipline.name}".

algo: Any¶: The interfaced machine learning algorithm.

der_function: Callable[[ndarray], ndarray]¶: The derivative of the radial basis function.

property function: str¶

The name of the kernel function.

The name is possibly different from self.parameters[‘function’], as it is mapped (scipy). Examples:

‘inverse’ -> ‘inverse_multiquadric’ ‘InverSE MULtiQuadRIC’ -> ‘inverse_multiquadric’

property input_data: ndarray¶: The input data matrix.

property input_dimension: int¶: The input space dimension.

input_names: list[str]¶: The names of the input variables.

input_space_center: dict[str, ndarray]¶: The center of the input space.

property is_trained: bool¶: Return whether the algorithm is trained.

property learning_samples_indices: Sequence[int]¶: The indices of the learning samples used for the training.

learning_set: Dataset¶: The learning dataset.

property output_data: ndarray¶: The output data matrix.

property output_dimension: int¶: The output space dimension.

output_names: list[str]¶: The names of the output variables.

parameters: dict[str, MLAlgoParameterType]¶: The parameters of the machine learning algorithm.

transformer: dict[str, Transformer]¶

The strategies to transform the variables, if any.

The values are instances of Transformer while the keys are the names of either the variables or the groups of variables, e.g. “inputs” or “outputs” in the case of the regression algorithms. If a group is specified, the Transformer will be applied to all the variables of this group.

y_average: ndarray¶: The mean of the learning output data.

Examples using RBFRegressor¶

Machine learning algorithm selection example

RBF regression

Save and Load