Note
Go to the end to download the full example code
Example for exterior penalty applied to the Sobieski test case.¶
This section describes how to set up and solve the MDO problem relative to the Sobieski test case with GEMSEO applying external penalty.
See also
To start with a simpler MDO problem, and for a detailed description of how to plug a test case into GEMSEO, see Tutorial: How to solve an MDO problem.
Solving with an MDF formulation¶
In this example, we solve the range optimization using the following MDF formulation:
The MDF formulation couples all the disciplines during the Multi Disciplinary Analyses at each optimization iteration.
All the design variables are equally treated, concatenated in a single vector and given to a single optimization algorithm as the unknowns of the problem.
There is no specific constraint due to the MDF formulation.
Only the design constraints \(g\_1\), \(g\_2\) and \(g\_3\) are added to the problem.
The objective function is the range (the \(y\_4\) variable in the model), computed after the Multi Disciplinary Analyses.
Imports¶
All the imports needed for the tutorials are performed here.
from __future__ import annotations
from gemseo import configure_logger
from gemseo import create_discipline
from gemseo import create_scenario
from gemseo import get_available_formulations
from gemseo.disciplines.utils import get_all_inputs
from gemseo.disciplines.utils import get_all_outputs
from gemseo.problems.mdo.sobieski.core.design_space import SobieskiDesignSpace
configure_logger()
<RootLogger root (INFO)>
Step 1: Creation of MDODiscipline¶
To build the scenario, we first instantiate the disciplines. Here, the disciplines themselves have already been developed and interfaced with GEMSEO (see Benchmark problems).
disciplines = create_discipline([
"SobieskiPropulsion",
"SobieskiAerodynamics",
"SobieskiMission",
"SobieskiStructure",
])
Tip
For the disciplines that are not interfaced with GEMSEO, the GEMSEO’s
gemseo eases the creation of disciplines without having
to import them.
Step 2: Creation of Scenario¶
The scenario delegates the creation of the optimization problem to the MDO formulation.
Therefore, it needs the list of disciplines, the names of the formulation,
the name of the objective function and the design space.
The
design_space(shown below for reference) defines the unknowns of the optimization problem, and their bounds. It contains all the design variables needed by the MDF formulation. It can be imported from a text file, or created from scratch with the methodscreate_design_space()andadd_variable(). In this case, we will useSobieskiDesignSpacealready defined in GEMSEO.
design_space = SobieskiDesignSpace()
x_0 = design_space.get_current_value(as_dict=True)
name lower_bound value upper_bound type
x_shared 0.01 0.05 0.09 float
x_shared 30000.0 45000.0 60000.0 float
x_shared 1.4 1.6 1.8 float
x_shared 2.5 5.5 8.5 float
x_shared 40.0 55.0 70.0 float
x_shared 500.0 1000.0 1500.0 float
x_1 0.1 0.25 0.4 float
x_1 0.75 1.0 1.25 float
x_2 0.75 1.0 1.25 float
x_3 0.1 0.5 1.0 float
y_14 24850.0 50606.9741711 77100.0 float
y_14 -7700.0 7306.20262124 45000.0 float
y_32 0.235 0.50279625 0.795 float
y_31 2960.0 6354.32430691 10185.0 float
y_24 0.44 4.15006276 11.13 float
y_34 0.44 1.10754577 1.98 float
y_23 3365.0 12194.2671934 26400.0 float
y_21 24850.0 50606.9741711 77250.0 float
y_12 24850.0 50606.9742 77250.0 float
y_12 0.45 0.95 1.5 float
The available MDO formulations are located in the gemseo.formulations package, see Extend GEMSEO features for extending GEMSEO with other formulations.
The
formulationclassname (here,"MDF") shall be passed to the scenario to select them.The list of available formulations can be obtained by using
get_available_formulations().
get_available_formulations()
['BiLevel', 'DisciplinaryOpt', 'IDF', 'MDF']
\(y\_4\) corresponds to the
objective_name. This name must be one of the disciplines outputs, here theSobieskiMissiondiscipline. The list of all outputs of the disciplines can be obtained by usingget_all_outputs():
get_all_outputs(disciplines)
get_all_inputs(disciplines)
['c_0', 'c_1', 'c_2', 'c_3', 'c_4', 'x_1', 'x_2', 'x_3', 'x_shared', 'y_12', 'y_14', 'y_21', 'y_23', 'y_24', 'y_31', 'y_32', 'y_34']
From these MDODiscipline, design space,
MDO formulation name and objective function name,
we build the scenario:
scenario = create_scenario(
disciplines,
"MDF",
"y_4",
design_space,
maximize_objective=True,
)
The range function (\(y\_4\)) should be maximized. However, optimizers
minimize functions by default. Which is why, when creating the scenario, the argument
maximize_objective shall be set to True.
Differentiation method¶
We may choose the way derivatives are computed:
Function derivatives. As analytical disciplinary derivatives are available for the Sobieski test-case, they can be used instead of computing the derivatives with finite-differences or with the complex-step method. The easiest way to set a method is to let the optimizer determine it:
scenario.set_differentiation_method()
The default behavior of the optimizer triggers finite differences. It corresponds to:
scenario.set_differentiation_method("finite_differences",1e-7)
It it also possible to differentiate functions by means of the complex step method:
scenario.set_differentiation_method("complex_step",1e-30j)
Constraints¶
Similarly to the objective function, the constraints names are a subset
of the disciplines’ outputs. They can be obtained by using
get_all_outputs().
The formulation has a powerful feature to automatically dispatch the constraints
(\(g\_1, g\_2, g\_3\)) and plug them to the optimizers depending on
the formulation. To do that, we use the method
add_constraint():
for constraint in ["g_1", "g_2", "g_3"]:
scenario.add_constraint(constraint, constraint_type="ineq")
Step 3: Apply the exterior penalty and execute the scenario¶
scenario.formulation.opt_problem.apply_exterior_penalty(
objective_scale=10.0, scale_inequality=10.0
)
In this way the L-BFGS-B algorithm can be used to solve the optimization problem. Note that this algorithm is not suited for constrained optimization problems.
algo_args = {"max_iter": 10, "algo": "L-BFGS-B"}
scenario.execute(algo_args)
INFO - 08:54:53:
INFO - 08:54:53: *** Start MDOScenario execution ***
INFO - 08:54:53: MDOScenario
INFO - 08:54:53: Disciplines: SobieskiAerodynamics SobieskiMission SobieskiPropulsion SobieskiStructure
INFO - 08:54:53: MDO formulation: MDF
INFO - 08:54:53: Optimization problem:
INFO - 08:54:53: minimize [[[[-y_4/10.0]+pos_sum_g_1]+pos_sum_g_2]+pos_sum_g_3](x_1, x_2, x_3, x_shared) = -y_4(x_shared, x_1, x_2, x_3)/10.0+sum(heaviside()***2)+sum(heaviside()***2)+sum(heaviside()***2)
INFO - 08:54:53: with respect to x_1, x_2, x_3, x_shared
INFO - 08:54:53: over the design space:
INFO - 08:54:53: +-------------+-------------+-------+-------------+-------+
INFO - 08:54:53: | Name | Lower bound | Value | Upper bound | Type |
INFO - 08:54:53: +-------------+-------------+-------+-------------+-------+
INFO - 08:54:53: | x_shared[0] | 0.01 | 0.05 | 0.09 | float |
INFO - 08:54:53: | x_shared[1] | 30000 | 45000 | 60000 | float |
INFO - 08:54:53: | x_shared[2] | 1.4 | 1.6 | 1.8 | float |
INFO - 08:54:53: | x_shared[3] | 2.5 | 5.5 | 8.5 | float |
INFO - 08:54:53: | x_shared[4] | 40 | 55 | 70 | float |
INFO - 08:54:53: | x_shared[5] | 500 | 1000 | 1500 | float |
INFO - 08:54:53: | x_1[0] | 0.1 | 0.25 | 0.4 | float |
INFO - 08:54:53: | x_1[1] | 0.75 | 1 | 1.25 | float |
INFO - 08:54:53: | x_2 | 0.75 | 1 | 1.25 | float |
INFO - 08:54:53: | x_3 | 0.1 | 0.5 | 1 | float |
INFO - 08:54:53: +-------------+-------------+-------+-------------+-------+
INFO - 08:54:53: Solving optimization problem with algorithm L-BFGS-B:
INFO - 08:54:53: 10%|█ | 1/10 [00:00<00:00, 10.49 it/sec, obj=-53.3]
INFO - 08:54:53: 20%|██ | 2/10 [00:00<00:01, 7.59 it/sec, obj=-401]
INFO - 08:54:53: 30%|███ | 3/10 [00:00<00:00, 7.18 it/sec, obj=103]
INFO - 08:54:54: 40%|████ | 4/10 [00:00<00:00, 6.80 it/sec, obj=-488]
INFO - 08:54:54: 50%|█████ | 5/10 [00:00<00:00, 6.55 it/sec, obj=-489]
INFO - 08:54:54: 60%|██████ | 6/10 [00:00<00:00, 6.40 it/sec, obj=-489]
INFO - 08:54:54: 70%|███████ | 7/10 [00:01<00:00, 6.30 it/sec, obj=-489]
INFO - 08:54:54: 80%|████████ | 8/10 [00:01<00:00, 6.22 it/sec, obj=-489]
INFO - 08:54:54: 90%|█████████ | 9/10 [00:01<00:00, 6.16 it/sec, obj=-489]
INFO - 08:54:55: 100%|██████████| 10/10 [00:01<00:00, 6.11 it/sec, obj=-489]
INFO - 08:54:55: Optimization result:
INFO - 08:54:55: Optimizer info:
INFO - 08:54:55: Status: None
INFO - 08:54:55: Message: Maximum number of iterations reached. GEMSEO Stopped the driver
INFO - 08:54:55: Number of calls to the objective function by the optimizer: 12
INFO - 08:54:55: Solution:
INFO - 08:54:55: Objective: -489.2416290389368
INFO - 08:54:55: Design space:
INFO - 08:54:55: +-------------+-------------+--------------------+-------------+-------+
INFO - 08:54:55: | Name | Lower bound | Value | Upper bound | Type |
INFO - 08:54:55: +-------------+-------------+--------------------+-------------+-------+
INFO - 08:54:55: | x_shared[0] | 0.01 | 0.09 | 0.09 | float |
INFO - 08:54:55: | x_shared[1] | 30000 | 60000 | 60000 | float |
INFO - 08:54:55: | x_shared[2] | 1.4 | 1.4 | 1.8 | float |
INFO - 08:54:55: | x_shared[3] | 2.5 | 2.5 | 8.5 | float |
INFO - 08:54:55: | x_shared[4] | 40 | 70 | 70 | float |
INFO - 08:54:55: | x_shared[5] | 500 | 1500 | 1500 | float |
INFO - 08:54:55: | x_1[0] | 0.1 | 0.248653494277963 | 0.4 | float |
INFO - 08:54:55: | x_1[1] | 0.75 | 0.75 | 1.25 | float |
INFO - 08:54:55: | x_2 | 0.75 | 0.75 | 1.25 | float |
INFO - 08:54:55: | x_3 | 0.1 | 0.2584061783719241 | 1 | float |
INFO - 08:54:55: +-------------+-------------+--------------------+-------------+-------+
INFO - 08:54:55: *** End MDOScenario execution (time: 0:00:01.755832) ***
{'max_iter': 10, 'algo': 'L-BFGS-B'}
Post-processing options¶
To visualize the optimization history of the constraint violation one can use the
BasicHistory:
scenario.post_process(
"BasicHistory", variable_names=["g_1", "g_2", "g_3"], save=False, show=True
)
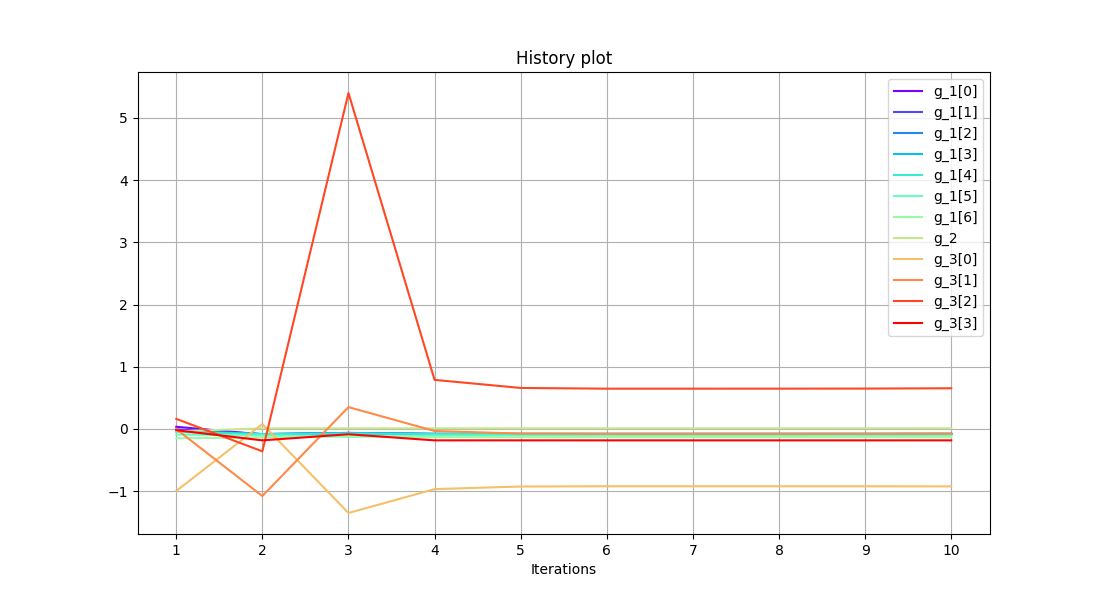
<gemseo.post.basic_history.BasicHistory object at 0x7f1df762df70>
This solution is almost feasible. The solution can better approximate the original problem solution increasing the value
of objective_scale and scale_inequality parameters.
Step 4: Rerun the scenario with increased penalty and objective scaling.¶
design_space.set_current_value(x_0)
scenario_2 = create_scenario(
disciplines,
"MDF",
"y_4",
design_space,
maximize_objective=True,
)
for constraint in ["g_1", "g_2", "g_3"]:
scenario_2.add_constraint(constraint, constraint_type="ineq")
scenario_2.set_differentiation_method()
scenario_2.formulation.opt_problem.apply_exterior_penalty(
objective_scale=1000.0, scale_inequality=1000.0
)
algo_args_2 = {"max_iter": 1000, "algo": "L-BFGS-B"}
scenario_2.execute(algo_args_2)
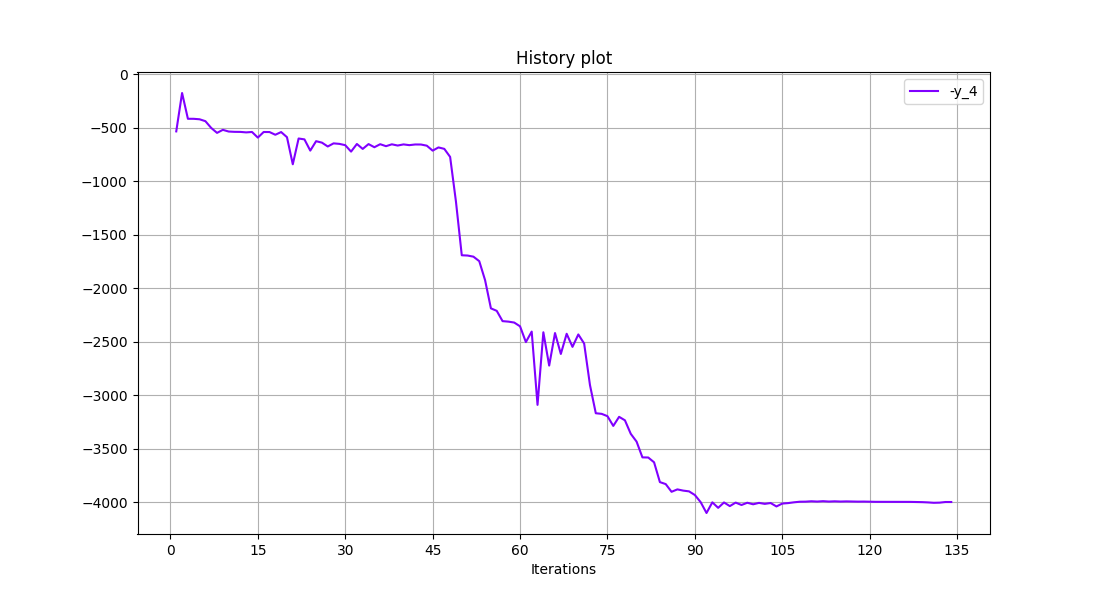
scenario_2.post_process("BasicHistory", variable_names=["-y_4"], save=False, show=True)
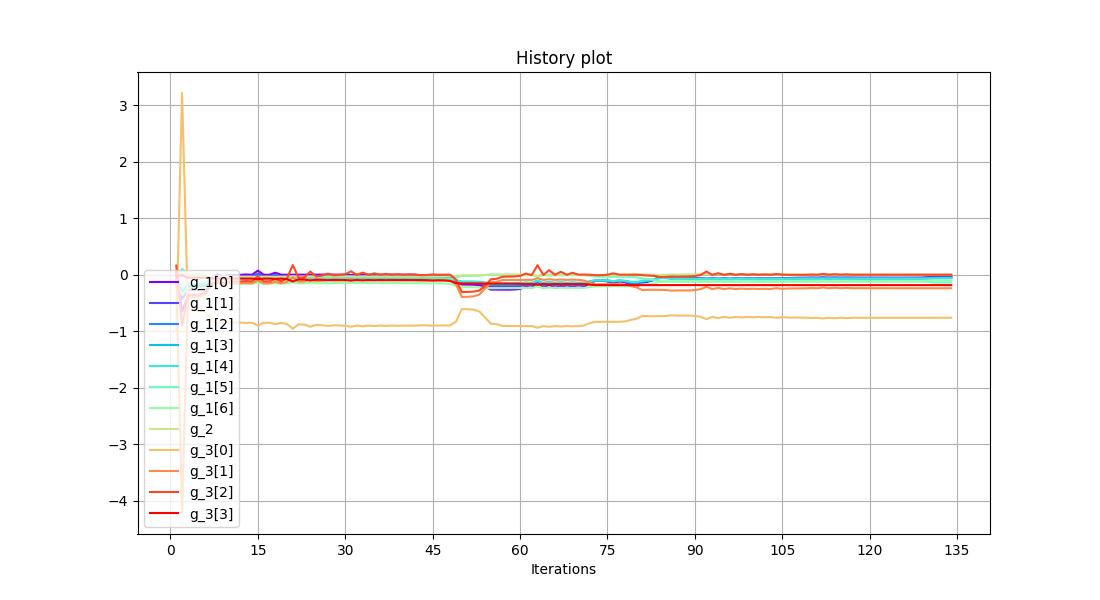
scenario_2.post_process(
"BasicHistory", variable_names=["g_1", "g_2", "g_3"], save=False, show=True
)
INFO - 08:54:55:
INFO - 08:54:55: *** Start MDOScenario execution ***
INFO - 08:54:55: MDOScenario
INFO - 08:54:55: Disciplines: SobieskiAerodynamics SobieskiMission SobieskiPropulsion SobieskiStructure
INFO - 08:54:55: MDO formulation: MDF
INFO - 08:54:55: Optimization problem:
INFO - 08:54:55: minimize [[[[-y_4/1000.0]+pos_sum_g_1]+pos_sum_g_2]+pos_sum_g_3](x_1, x_2, x_3, x_shared) = -y_4(x_shared, x_1, x_2, x_3)/1000.0+sum(heaviside()***2)+sum(heaviside()***2)+sum(heaviside()***2)
INFO - 08:54:55: with respect to x_1, x_2, x_3, x_shared
INFO - 08:54:55: over the design space:
INFO - 08:54:55: +-------------+-------------+-------+-------------+-------+
INFO - 08:54:55: | Name | Lower bound | Value | Upper bound | Type |
INFO - 08:54:55: +-------------+-------------+-------+-------------+-------+
INFO - 08:54:55: | x_shared[0] | 0.01 | 0.05 | 0.09 | float |
INFO - 08:54:55: | x_shared[1] | 30000 | 45000 | 60000 | float |
INFO - 08:54:55: | x_shared[2] | 1.4 | 1.6 | 1.8 | float |
INFO - 08:54:55: | x_shared[3] | 2.5 | 5.5 | 8.5 | float |
INFO - 08:54:55: | x_shared[4] | 40 | 55 | 70 | float |
INFO - 08:54:55: | x_shared[5] | 500 | 1000 | 1500 | float |
INFO - 08:54:55: | x_1[0] | 0.1 | 0.25 | 0.4 | float |
INFO - 08:54:55: | x_1[1] | 0.75 | 1 | 1.25 | float |
INFO - 08:54:55: | x_2 | 0.75 | 1 | 1.25 | float |
INFO - 08:54:55: | x_3 | 0.1 | 0.5 | 1 | float |
INFO - 08:54:55: +-------------+-------------+-------+-------------+-------+
INFO - 08:54:55: Solving optimization problem with algorithm L-BFGS-B:
INFO - 08:54:56: 1%| | 6/1000 [00:00<02:29, 6.65 it/sec, obj=-0.428]
INFO - 08:54:56: 1%| | 7/1000 [00:01<02:29, 6.65 it/sec, obj=-0.504]
INFO - 08:54:56: 1%| | 8/1000 [00:01<02:28, 6.69 it/sec, obj=-0.413]
INFO - 08:54:56: 1%| | 9/1000 [00:01<02:27, 6.72 it/sec, obj=-0.521]
INFO - 08:54:57: 1%| | 10/1000 [00:01<02:26, 6.76 it/sec, obj=-0.537]
INFO - 08:54:57: 1%| | 11/1000 [00:01<02:25, 6.79 it/sec, obj=-0.54]
INFO - 08:54:57: 1%| | 12/1000 [00:01<02:25, 6.79 it/sec, obj=-0.541]
INFO - 08:54:57: 1%|▏ | 13/1000 [00:01<02:25, 6.80 it/sec, obj=-0.521]
INFO - 08:54:57: 1%|▏ | 14/1000 [00:02<02:24, 6.80 it/sec, obj=-0.541]
INFO - 08:54:57: 2%|▏ | 15/1000 [00:02<02:25, 6.79 it/sec, obj=4.92]
INFO - 08:54:57: 2%|▏ | 16/1000 [00:02<02:24, 6.80 it/sec, obj=-0.542]
INFO - 08:54:58: 2%|▏ | 17/1000 [00:02<02:24, 6.82 it/sec, obj=-0.542]
INFO - 08:54:58: 2%|▏ | 18/1000 [00:02<02:23, 6.83 it/sec, obj=0.751]
INFO - 08:54:58: 2%|▏ | 19/1000 [00:02<02:23, 6.84 it/sec, obj=-0.542]
INFO - 08:54:58: 2%|▏ | 20/1000 [00:02<02:23, 6.84 it/sec, obj=-0.589]
INFO - 08:54:58: 2%|▏ | 21/1000 [00:03<02:23, 6.82 it/sec, obj=28.5]
INFO - 08:54:58: 2%|▏ | 22/1000 [00:03<02:23, 6.82 it/sec, obj=-0.601]
INFO - 08:54:58: 2%|▏ | 23/1000 [00:03<02:23, 6.82 it/sec, obj=-0.609]
INFO - 08:54:59: 2%|▏ | 24/1000 [00:03<02:23, 6.81 it/sec, obj=2.4]
INFO - 08:54:59: 2%|▎ | 25/1000 [00:03<02:23, 6.80 it/sec, obj=-0.625]
INFO - 08:54:59: 3%|▎ | 26/1000 [00:03<02:23, 6.80 it/sec, obj=-0.639]
INFO - 08:54:59: 3%|▎ | 27/1000 [00:03<02:23, 6.79 it/sec, obj=-0.311]
INFO - 08:54:59: 3%|▎ | 28/1000 [00:04<02:23, 6.78 it/sec, obj=-0.645]
INFO - 08:54:59: 3%|▎ | 29/1000 [00:04<02:23, 6.78 it/sec, obj=-0.65]
INFO - 08:54:59: 3%|▎ | 30/1000 [00:04<02:23, 6.78 it/sec, obj=-0.611]
INFO - 08:55:00: 3%|▎ | 31/1000 [00:04<02:23, 6.77 it/sec, obj=2.98]
INFO - 08:55:00: 3%|▎ | 32/1000 [00:04<02:23, 6.76 it/sec, obj=-0.651]
INFO - 08:55:00: 3%|▎ | 33/1000 [00:04<02:23, 6.76 it/sec, obj=0.77]
INFO - 08:55:00: 3%|▎ | 34/1000 [00:05<02:22, 6.76 it/sec, obj=-0.652]
INFO - 08:55:00: 4%|▎ | 35/1000 [00:05<02:22, 6.75 it/sec, obj=-0.103]
INFO - 08:55:00: 4%|▎ | 36/1000 [00:05<02:22, 6.75 it/sec, obj=-0.654]
INFO - 08:55:01: 4%|▎ | 37/1000 [00:05<02:22, 6.75 it/sec, obj=-0.444]
INFO - 08:55:01: 4%|▍ | 38/1000 [00:05<02:22, 6.75 it/sec, obj=-0.655]
INFO - 08:55:01: 4%|▍ | 39/1000 [00:05<02:22, 6.74 it/sec, obj=-0.574]
INFO - 08:55:01: 4%|▍ | 40/1000 [00:05<02:22, 6.74 it/sec, obj=-0.656]
INFO - 08:55:01: 4%|▍ | 41/1000 [00:06<02:22, 6.74 it/sec, obj=-0.624]
INFO - 08:55:01: 4%|▍ | 42/1000 [00:06<02:22, 6.74 it/sec, obj=-0.657]
INFO - 08:55:01: 4%|▍ | 43/1000 [00:06<02:22, 6.74 it/sec, obj=-0.658]
INFO - 08:55:02: 4%|▍ | 44/1000 [00:06<02:21, 6.74 it/sec, obj=-0.669]
INFO - 08:55:02: 4%|▍ | 45/1000 [00:06<02:21, 6.73 it/sec, obj=-0.68]
INFO - 08:55:02: 5%|▍ | 46/1000 [00:06<02:21, 6.73 it/sec, obj=-0.686]
INFO - 08:55:02: 5%|▍ | 47/1000 [00:06<02:21, 6.73 it/sec, obj=-0.694]
INFO - 08:55:02: 5%|▍ | 48/1000 [00:07<02:21, 6.72 it/sec, obj=-0.774]
INFO - 08:55:02: 5%|▍ | 49/1000 [00:07<02:21, 6.70 it/sec, obj=-1.19]
INFO - 08:55:03: 5%|▌ | 50/1000 [00:07<02:22, 6.66 it/sec, obj=-1.69]
INFO - 08:55:03: 5%|▌ | 51/1000 [00:07<02:23, 6.63 it/sec, obj=-1.7]
INFO - 08:55:03: 5%|▌ | 52/1000 [00:07<02:23, 6.59 it/sec, obj=-1.71]
INFO - 08:55:03: 5%|▌ | 53/1000 [00:08<02:24, 6.56 it/sec, obj=-1.75]
INFO - 08:55:03: 5%|▌ | 54/1000 [00:08<02:24, 6.54 it/sec, obj=-1.93]
INFO - 08:55:03: 6%|▌ | 55/1000 [00:08<02:24, 6.53 it/sec, obj=-2.17]
INFO - 08:55:04: 6%|▌ | 56/1000 [00:08<02:24, 6.51 it/sec, obj=-2.19]
INFO - 08:55:04: 6%|▌ | 57/1000 [00:08<02:25, 6.50 it/sec, obj=-2.28]
INFO - 08:55:04: 6%|▌ | 58/1000 [00:08<02:25, 6.49 it/sec, obj=-2.29]
INFO - 08:55:04: 6%|▌ | 59/1000 [00:09<02:25, 6.48 it/sec, obj=-2.3]
INFO - 08:55:04: 6%|▌ | 60/1000 [00:09<02:25, 6.47 it/sec, obj=-2.35]
INFO - 08:55:05: 6%|▌ | 61/1000 [00:09<02:25, 6.46 it/sec, obj=-2.1]
INFO - 08:55:05: 6%|▌ | 62/1000 [00:09<02:25, 6.45 it/sec, obj=-2.4]
INFO - 08:55:05: 6%|▋ | 63/1000 [00:09<02:25, 6.43 it/sec, obj=25.5]
INFO - 08:55:05: 6%|▋ | 64/1000 [00:09<02:25, 6.42 it/sec, obj=-2.41]
INFO - 08:55:05: 6%|▋ | 65/1000 [00:10<02:25, 6.41 it/sec, obj=3.96]
INFO - 08:55:05: 7%|▋ | 66/1000 [00:10<02:25, 6.40 it/sec, obj=-2.42]
INFO - 08:55:06: 7%|▋ | 67/1000 [00:10<02:26, 6.39 it/sec, obj=0.179]
INFO - 08:55:06: 7%|▋ | 68/1000 [00:10<02:26, 6.38 it/sec, obj=-2.43]
INFO - 08:55:06: 7%|▋ | 69/1000 [00:10<02:26, 6.37 it/sec, obj=-1.35]
INFO - 08:55:06: 7%|▋ | 70/1000 [00:10<02:26, 6.37 it/sec, obj=-2.43]
INFO - 08:55:06: 7%|▋ | 71/1000 [00:11<02:26, 6.36 it/sec, obj=-2.51]
INFO - 08:55:06: 7%|▋ | 72/1000 [00:11<02:26, 6.36 it/sec, obj=-2.9]
INFO - 08:55:07: 7%|▋ | 73/1000 [00:11<02:26, 6.35 it/sec, obj=-3.17]
INFO - 08:55:07: 7%|▋ | 74/1000 [00:11<02:26, 6.34 it/sec, obj=-3.17]
INFO - 08:55:07: 8%|▊ | 75/1000 [00:11<02:26, 6.33 it/sec, obj=-3.2]
INFO - 08:55:07: 8%|▊ | 76/1000 [00:12<02:26, 6.32 it/sec, obj=-2.72]
INFO - 08:55:07: 8%|▊ | 77/1000 [00:12<02:26, 6.31 it/sec, obj=-3.2]
INFO - 08:55:07: 8%|▊ | 78/1000 [00:12<02:26, 6.30 it/sec, obj=-3.23]
INFO - 08:55:08: 8%|▊ | 79/1000 [00:12<02:26, 6.30 it/sec, obj=-3.35]
INFO - 08:55:08: 8%|▊ | 80/1000 [00:12<02:26, 6.29 it/sec, obj=-3.38]
INFO - 08:55:08: 8%|▊ | 81/1000 [00:12<02:26, 6.28 it/sec, obj=-3.54]
INFO - 08:55:08: 8%|▊ | 82/1000 [00:13<02:26, 6.27 it/sec, obj=-3.58]
INFO - 08:55:08: 8%|▊ | 83/1000 [00:13<02:26, 6.27 it/sec, obj=-3.63]
INFO - 08:55:08: 8%|▊ | 84/1000 [00:13<02:26, 6.25 it/sec, obj=-3.81]
INFO - 08:55:09: 8%|▊ | 85/1000 [00:13<02:26, 6.24 it/sec, obj=-3.83]
INFO - 08:55:09: 9%|▊ | 86/1000 [00:13<02:26, 6.24 it/sec, obj=-3.87]
INFO - 08:55:09: 9%|▊ | 87/1000 [00:13<02:26, 6.23 it/sec, obj=-3.87]
INFO - 08:55:09: 9%|▉ | 88/1000 [00:14<02:26, 6.22 it/sec, obj=-3.88]
INFO - 08:55:09: 9%|▉ | 89/1000 [00:14<02:26, 6.22 it/sec, obj=-3.88]
INFO - 08:55:10: 9%|▉ | 90/1000 [00:14<02:26, 6.21 it/sec, obj=-3.89]
INFO - 08:55:10: 9%|▉ | 91/1000 [00:14<02:26, 6.21 it/sec, obj=-3.92]
INFO - 08:55:10: 9%|▉ | 92/1000 [00:14<02:26, 6.20 it/sec, obj=-0.827]
INFO - 08:55:10: 9%|▉ | 93/1000 [00:15<02:26, 6.20 it/sec, obj=-3.93]
INFO - 08:55:10: 9%|▉ | 94/1000 [00:15<02:26, 6.19 it/sec, obj=-3.24]
INFO - 08:55:10: 10%|▉ | 95/1000 [00:15<02:26, 6.18 it/sec, obj=-3.93]
INFO - 08:55:11: 10%|▉ | 96/1000 [00:15<02:26, 6.18 it/sec, obj=-3.65]
INFO - 08:55:11: 10%|▉ | 97/1000 [00:15<02:26, 6.17 it/sec, obj=-3.93]
INFO - 08:55:11: 10%|▉ | 98/1000 [00:15<02:26, 6.16 it/sec, obj=-3.82]
INFO - 08:55:11: 10%|▉ | 99/1000 [00:16<02:26, 6.15 it/sec, obj=-3.93]
INFO - 08:55:11: 10%|█ | 100/1000 [00:16<02:26, 6.15 it/sec, obj=-3.89]
INFO - 08:55:12: 10%|█ | 101/1000 [00:16<02:26, 6.14 it/sec, obj=-3.93]
INFO - 08:55:12: 10%|█ | 102/1000 [00:16<02:26, 6.14 it/sec, obj=-3.91]
INFO - 08:55:12: 10%|█ | 103/1000 [00:16<02:26, 6.13 it/sec, obj=-3.93]
INFO - 08:55:12: 10%|█ | 104/1000 [00:16<02:26, 6.12 it/sec, obj=-3.82]
INFO - 08:55:12: 10%|█ | 105/1000 [00:17<02:26, 6.11 it/sec, obj=-3.93]
INFO - 08:55:12: 11%|█ | 106/1000 [00:17<02:26, 6.11 it/sec, obj=-3.97]
INFO - 08:55:13: 11%|█ | 107/1000 [00:17<02:26, 6.11 it/sec, obj=-3.98]
INFO - 08:55:13: 11%|█ | 108/1000 [00:17<02:26, 6.11 it/sec, obj=-3.98]
INFO - 08:55:13: 11%|█ | 109/1000 [00:17<02:26, 6.10 it/sec, obj=-3.98]
INFO - 08:55:13: 11%|█ | 110/1000 [00:18<02:25, 6.10 it/sec, obj=-3.97]
INFO - 08:55:13: 11%|█ | 111/1000 [00:18<02:25, 6.09 it/sec, obj=-3.98]
INFO - 08:55:13: 11%|█ | 112/1000 [00:18<02:25, 6.09 it/sec, obj=-3.79]
INFO - 08:55:14: 11%|█▏ | 113/1000 [00:18<02:25, 6.09 it/sec, obj=-3.98]
INFO - 08:55:14: 11%|█▏ | 114/1000 [00:18<02:25, 6.09 it/sec, obj=-3.9]
INFO - 08:55:14: 12%|█▏ | 115/1000 [00:18<02:25, 6.08 it/sec, obj=-3.98]
INFO - 08:55:14: 12%|█▏ | 116/1000 [00:19<02:25, 6.08 it/sec, obj=-3.95]
INFO - 08:55:14: 12%|█▏ | 117/1000 [00:19<02:25, 6.08 it/sec, obj=-3.98]
INFO - 08:55:14: 12%|█▏ | 118/1000 [00:19<02:25, 6.07 it/sec, obj=-3.98]
INFO - 08:55:15: 12%|█▏ | 119/1000 [00:19<02:25, 6.07 it/sec, obj=-3.98]
INFO - 08:55:15: 12%|█▏ | 120/1000 [00:19<02:25, 6.07 it/sec, obj=-3.98]
INFO - 08:55:15: 12%|█▏ | 121/1000 [00:19<02:24, 6.06 it/sec, obj=-3.98]
INFO - 08:55:15: 12%|█▏ | 122/1000 [00:20<02:24, 6.06 it/sec, obj=-3.98]
INFO - 08:55:15: 12%|█▏ | 123/1000 [00:20<02:24, 6.06 it/sec, obj=-3.98]
INFO - 08:55:16: 12%|█▏ | 124/1000 [00:20<02:24, 6.05 it/sec, obj=-3.98]
INFO - 08:55:16: 12%|█▎ | 125/1000 [00:20<02:24, 6.05 it/sec, obj=-3.98]
INFO - 08:55:16: 13%|█▎ | 126/1000 [00:20<02:24, 6.05 it/sec, obj=-3.98]
INFO - 08:55:16: 13%|█▎ | 127/1000 [00:21<02:24, 6.05 it/sec, obj=-3.98]
INFO - 08:55:16: 13%|█▎ | 128/1000 [00:21<02:24, 6.05 it/sec, obj=-3.98]
INFO - 08:55:16: 13%|█▎ | 129/1000 [00:21<02:24, 6.04 it/sec, obj=-3.98]
INFO - 08:55:17: 13%|█▎ | 130/1000 [00:21<02:24, 6.04 it/sec, obj=-3.98]
INFO - 08:55:17: 13%|█▎ | 131/1000 [00:21<02:23, 6.04 it/sec, obj=-3.98]
INFO - 08:55:17: 13%|█▎ | 132/1000 [00:21<02:23, 6.03 it/sec, obj=-3.98]
INFO - 08:55:17: 13%|█▎ | 133/1000 [00:22<02:23, 6.03 it/sec, obj=-3.98]
INFO - 08:55:17: 13%|█▎ | 134/1000 [00:22<02:23, 6.03 it/sec, obj=-3.98]
INFO - 08:55:17: Optimization result:
INFO - 08:55:17: Optimizer info:
INFO - 08:55:17: Status: 0
INFO - 08:55:17: Message: CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
INFO - 08:55:17: Number of calls to the objective function by the optimizer: 136
INFO - 08:55:17: Solution:
INFO - 08:55:17: Objective: -3.9803860964876963
INFO - 08:55:17: Design space:
INFO - 08:55:17: +-------------+-------------+---------------------+-------------+-------+
INFO - 08:55:17: | Name | Lower bound | Value | Upper bound | Type |
INFO - 08:55:17: +-------------+-------------+---------------------+-------------+-------+
INFO - 08:55:17: | x_shared[0] | 0.01 | 0.06101561365627294 | 0.09 | float |
INFO - 08:55:17: | x_shared[1] | 30000 | 60000 | 60000 | float |
INFO - 08:55:17: | x_shared[2] | 1.4 | 1.4 | 1.8 | float |
INFO - 08:55:17: | x_shared[3] | 2.5 | 2.5 | 8.5 | float |
INFO - 08:55:17: | x_shared[4] | 40 | 70 | 70 | float |
INFO - 08:55:17: | x_shared[5] | 500 | 1500 | 1500 | float |
INFO - 08:55:17: | x_1[0] | 0.1 | 0.4 | 0.4 | float |
INFO - 08:55:17: | x_1[1] | 0.75 | 0.75 | 1.25 | float |
INFO - 08:55:17: | x_2 | 0.75 | 0.75 | 1.25 | float |
INFO - 08:55:17: | x_3 | 0.1 | 0.1562913023426308 | 1 | float |
INFO - 08:55:17: +-------------+-------------+---------------------+-------------+-------+
INFO - 08:55:17: *** End MDOScenario execution (time: 0:00:22.339392) ***
<gemseo.post.basic_history.BasicHistory object at 0x7f1dd36a3c10>
The solution feasibility was improved but this comes with a much higher number of iterations.
Total running time of the script: (0 minutes 24.871 seconds)