parametric module¶

Class for the parametric estimation of statistics from a dataset.

Overview¶

The ParametricStatistics class inherits from the abstract Statistics class and aims to estimate statistics from a Dataset, based on candidate parametric distributions calibrated from this Dataset.

For each variable,

the parameters of these distributions are calibrated from the Dataset,
the fitted parametric Distribution which is optimal in the sense of a goodness-of-fit criterion and a selection criterion is selected to estimate the statistics related to this variable.

The ParametricStatistics relies on the OpenTURNS library through the OTDistribution and OTDistributionFitter classes.

Construction¶

The ParametricStatistics is built from two mandatory arguments:

a dataset,
a list of distributions names,

and can consider optional arguments:

a subset of variables names (by default, statistics are computed for all variables),
a fitting criterion name (by default, BIC is used; see FittingCriterion and SignificanceTest for more information),
a level associated with the fitting criterion,
a selection criterion:
- ‘best’: select the distribution minimizing (or maximizing, depending on the criterion) the criterion,
- ‘first’: select the first distribution for which the criterion is greater (or lower, depending on the criterion) than the level,
a name for the ParametricStatistics object (by default, the name is the concatenation of ‘ParametricStatistics’ and the name of the Dataset).

Capabilities¶

By inheritance, a ParametricStatistics object has the same capabilities as Statistics. Additional ones are:

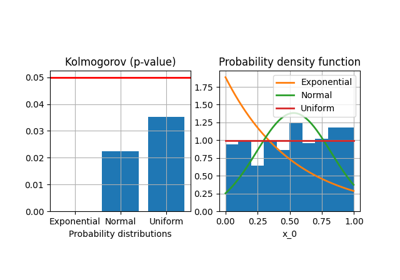
get_fitting_matrix(): this method displays the values of the fitting criterion for the different variables and candidate probability distributions as well as the select probability distribution,
plot_criteria(): this method plots the criterion values for a given variable.

class gemseo.uncertainty.statistics.parametric.ParametricStatistics(dataset, distributions, variable_names=(), fitting_criterion=FittingCriterion.BIC, level=0.05, selection_criterion=SelectionCriterion.BEST, name='')[source]

Bases: Statistics

A toolbox to compute statistics based on probability distribution-fitting.

Unless otherwise stated, the statistics are computed variable-wise and component-wise, i.e. variable-by-variable and component-by-component. So, for the sake of readability, the methods named as compute_statistic() return dict[str, ndarray] objects whose values are the names of the variables and the values are the statistic estimated for the different component.

Examples

>>> from gemseo import (
...     create_discipline,
...     create_parameter_space,
...     create_scenario
... )
>>> from gemseo.uncertainty.statistics.parametric import ParametricStatistics
>>>
>>> expressions = {"y1": "x1+2*x2", "y2": "x1-3*x2"}
>>> discipline = create_discipline(
...     "AnalyticDiscipline", expressions=expressions
... )
>>>
>>> parameter_space = create_parameter_space()
>>> parameter_space.add_random_variable(
...     "x1", "OTUniformDistribution", minimum=-1, maximum=1
... )
>>> parameter_space.add_random_variable(
...     "x2", "OTNormalDistribution", mu=0.5, sigma=2
... )
>>>
>>> scenario = create_scenario(
...     [discipline],
...     "DisciplinaryOpt",
...     "y1", parameter_space, scenario_type="DOE"
... )
>>> scenario.execute({'algo': 'OT_MONTE_CARLO', 'n_samples': 100})
>>>
>>> dataset = scenario.to_dataset(opt_naming=False)
>>>
>>> statistics = ParametricStatistics(
...     dataset, ['Normal', 'Uniform', 'Triangular']
... )
>>> fitting_matrix = statistics.get_fitting_matrix()
>>> mean = statistics.compute_mean()

Parameters:

dataset (Dataset) – A dataset.
distributions (Sequence[DistributionName]) – The names of the distributions.
variable_names (Iterable[str]) –
The names of the variables for which to compute statistics. If empty, consider all the variables of the dataset.

By default it is set to ().
fitting_criterion (FittingCriterion) –
The name of the goodness-of-fit criterion, measuring how the distribution fits the data. Use ParametricStatistics.get_criteria() to get the available criteria.

By default it is set to “BIC”.
level (float) –
A test level, i.e. the risk of committing a Type 1 error, that is an incorrect rejection of a true null hypothesis, for criteria based on test hypothesis.

By default it is set to 0.05.
selection_criterion (SelectionCriterion) –
The selection criterion to select a distribution from a list of candidates.

By default it is set to “best”.
name (str) –
A name for the toolbox computing statistics. If empty, concatenate the names of the dataset and the name of the class.

By default it is set to “”.

class DistributionName(value)

Bases: StrEnum

An enumeration.

Arcsine = 'Arcsine'

Beta = 'Beta'

Burr = 'Burr'

Chi = 'Chi'

ChiSquare = 'ChiSquare'

Dirichlet = 'Dirichlet'

Exponential = 'Exponential'

FisherSnedecor = 'FisherSnedecor'

Frechet = 'Frechet'

Gamma = 'Gamma'

GeneralizedPareto = 'GeneralizedPareto'

Gumbel = 'Gumbel'

Histogram = 'Histogram'

InverseNormal = 'InverseNormal'

Laplace = 'Laplace'

LogNormal = 'LogNormal'

LogUniform = 'LogUniform'

Logistic = 'Logistic'

MeixnerDistribution = 'MeixnerDistribution'

Normal = 'Normal'

Pareto = 'Pareto'

Rayleigh = 'Rayleigh'

Rice = 'Rice'

Student = 'Student'

Trapezoidal = 'Trapezoidal'

Triangular = 'Triangular'

TruncatedNormal = 'TruncatedNormal'

Uniform = 'Uniform'

VonMises = 'VonMises'

WeibullMax = 'WeibullMax'

WeibullMin = 'WeibullMin'

class FittingCriterion(value)

Bases: StrEnum

An enumeration.

BIC = 'BIC'

ChiSquared = 'ChiSquared'

Kolmogorov = 'Kolmogorov'

class SelectionCriterion(value)

Bases: LowercaseStrEnum

An enumeration.

BEST = 'best'

FIRST = 'first'

class SignificanceTest(value)

Bases: StrEnum

An enumeration.

ChiSquared = 'ChiSquared'

Kolmogorov = 'Kolmogorov'

compute_joint_probability(thresh, greater=True)[source]

Compute the joint probability related to a threshold.

Either \(\mathbb{P}[X \geq x]\) or \(\mathbb{P}[X \leq x]\).

Parameters:

thresh (Mapping[str, float | ndarray]) – A threshold \(x\) per variable.
greater (bool) –
The type of probability. If True, compute the probability of exceeding the threshold. Otherwise, compute the opposite.

By default it is set to True.

Returns:

The joint probability of the different variables (by definition of the joint probability, this statistics is not computed component-wise).

Return type:

dict[str, float]

compute_maximum()[source]

Compute the maximum \(\text{Max}[X]\).

Returns:: The component-wise maximum of the different variables.
Return type:: dict[str, numpy.ndarray]

compute_mean()[source]

Compute the mean \(\mathbb{E}[X]\).

Returns:: The component-wise mean of the different variables.
Return type:: dict[str, numpy.ndarray]

compute_minimum()[source]

Compute the \(\text{Min}[X]\).

Returns:: The component-wise minimum of the different variables.
Return type:: dict[str, numpy.ndarray]

compute_moment(order)[source]

Compute the n-th moment \(M[X; n]\).

Parameters:: order (int) – The order \(n\) of the moment.
Returns:: The component-wise moment of the different variables.
Return type:: dict[str, numpy.ndarray]

compute_probability(thresh, greater=True)[source]

Compute the probability related to a threshold.

Either \(\mathbb{P}[X \geq x]\) or \(\mathbb{P}[X \leq x]\).

Parameters:

thresh (Mapping[str, float | ndarray]) – A threshold \(x\) per variable.
greater (bool) –
The type of probability. If True, compute the probability of exceeding the threshold. Otherwise, compute the opposite.

By default it is set to True.

Returns:

The component-wise probability of the different variables.

Return type:

dict[str, ndarray]

compute_quantile(prob)[source]

Compute the quantile \(\mathbb{Q}[X; \alpha]\) related to a probability.

Parameters:: prob (float) – A probability \(\alpha\) between 0 and 1.
Returns:: The component-wise quantile of the different variables.
Return type:: dict[str, numpy.ndarray]

compute_range()[source]

Compute the range \(R[X]\).

Returns:: The component-wise range of the different variables.
Return type:: dict[str, numpy.ndarray]

compute_standard_deviation()[source]

Compute the standard deviation \(\mathbb{S}[X]\).

Returns:: The component-wise standard deviation of the different variables.
Return type:: dict[str, numpy.ndarray]

compute_tolerance_interval(coverage, confidence=0.95, side=ToleranceIntervalSide.BOTH)[source]

Compute a \((p,1-\alpha)\) tolerance interval \(\text{TI}[X]\).

The tolerance interval \(\text{TI}[X]\) is defined to contain at least a proportion \(p\) of the values of \(X\) with a level of confidence \(1-\alpha\). \(p\) is also called the coverage level of the TI.

Typically, \(\alpha=0.05\) or equivalently \(1-\alpha=0.95\).

The tolerance interval can be either

lower-sided (side="LOWER": \([L, +\infty[\)),
upper-sided (side="UPPER": \(]-\infty, U]\)) or
both-sided (side="BOTH": \([L, U]\)).

Parameters:

coverage (float) – A minimum proportion \(p\in[0,1]\) of belonging to the TI.
confidence (float) –
A level of confidence \(1-\alpha\in[0,1]\).

By default it is set to 0.95.
side (ToleranceIntervalSide) –
The type of the tolerance interval.

By default it is set to “both”.

Returns:

The component-wise tolerance intervals of the different variables, expressed as {variable_name: [(lower_bound, upper_bound), ...], ... } where [(lower_bound, upper_bound), ...] are the lower and upper bounds of the tolerance interval of the different components of variable_name.

Return type:

dict[str, list[gemseo.uncertainty.statistics.tolerance_interval.distribution.ToleranceInterval.Bounds]]

Examples using ParametricStatistics¶

Parametric estimation of statistics