Note
Go to the end to download the full example code.
A from scratch example on the Sellar problem#
Introduction#
In this example,
we will create an MDO scenario based on the Sellar's problem from scratch.
Contrary to the GEMSEO in 10 minutes,
all the disciplines will be implemented from scratch
by sub-classing the Discipline class
for each discipline of the Sellar problem.
The Sellar problem#
We will consider in this example the Sellar problem:
where the coupling variables are
and
and where the general constraints are
Imports#
All the imports needed for the tutorials are performed here.
from __future__ import annotations
from math import exp
from typing import TYPE_CHECKING
from numpy import array
from numpy import ones
from gemseo import configure_logger
from gemseo import create_scenario
from gemseo.algos.design_space import DesignSpace
from gemseo.core.discipline import Discipline
if TYPE_CHECKING:
from gemseo.typing import StrKeyMapping
configure_logger()
<RootLogger root (INFO)>
Create the disciplinary classes#
In this section,
we define the Sellar disciplines by sub-classing the Discipline class.
For each class,
the constructor and the _run method are overriden:
In the constructor, the input and output grammar are created. They define which inputs and outputs variables are allowed at the discipline execution. The default inputs are also defined, in case of the user does not provide them at the discipline execution.
In the _run method is implemented the concrete computation of the discipline. The returned NumPy arrays can then be used to compute the output values. They can then be stored in the
Discipline.datadictionary. If the discipline execution is successful.
Note that we do not define the Jacobians in the disciplines. In this example, we will approximate the derivatives using the finite differences method.
Create the SellarSystem class#
class SellarSystem(Discipline):
def __init__(self) -> None:
super().__init__()
# Initialize the grammars to define inputs and outputs
self.input_grammar.update_from_names(["x", "z", "y_1", "y_2"])
self.output_grammar.update_from_names(["obj", "c_1", "c_2"])
# Default inputs define what data to use when the inputs are not
# provided to the execute method
self.default_input_data = {
"x": ones(1),
"z": array([4.0, 3.0]),
"y_1": ones(1),
"y_2": ones(1),
}
def _run(self, input_data: StrKeyMapping) -> StrKeyMapping | None:
# The run method defines what happens at execution
# ie how outputs are computed from inputs
x = input_data["x"]
z = input_data["z"]
y_1 = input_data["y_1"]
y_2 = input_data["y_2"]
# The ouputs are stored here
output_data = {}
output_data["obj"] = array([x[0] ** 2 + z[1] + y_1[0] ** 2 + exp(-y_2[0])])
output_data["c_1"] = array([3.16 - y_1[0] ** 2])
output_data["c_2"] = array([y_2[0] - 24.0])
return output_data
Create the Sellar1 class#
class Sellar1(Discipline):
def __init__(self) -> None:
super().__init__()
self.input_grammar.update_from_names(["x", "z", "y_2"])
self.output_grammar.update_from_names(["y_1"])
self.default_input_data = {
"x": ones(1),
"z": array([4.0, 3.0]),
"y_2": ones(1),
}
def _run(self, input_data: StrKeyMapping) -> StrKeyMapping | None:
x = input_data["x"]
z = input_data["z"]
y_2 = input_data["y_2"]
return {"y_1": array([(z[0] ** 2 + z[1] + x[0] - 0.2 * y_2[0]) ** 0.5])}
Create the Sellar2 class#
class Sellar2(Discipline):
def __init__(self) -> None:
super().__init__()
self.input_grammar.update_from_names(["z", "y_1"])
self.output_grammar.update_from_names(["y_2"])
self.default_input_data = {
"z": array([4.0, 3.0]),
"y_1": ones(1),
}
def _run(self, input_data: StrKeyMapping) -> StrKeyMapping | None:
z = input_data["z"]
y_1 = input_data["y_1"]
return {"y_2": array([abs(y_1[0]) + z[0] + z[1]])}
Create and execute the scenario#
Instantiate disciplines#
We can now instantiate the disciplines and store the instances in a list which will be used below.
disciplines = [Sellar1(), Sellar2(), SellarSystem()]
Create the design space#
In this section, we define the design space which will be used for the creation of the MDOScenario. Note that the coupling variables are defined in the design space. Indeed, as we are going to select the IDF formulation to solve the MDO scenario, the coupling variables will be unknowns of the optimization problem and consequently they have to be included in the design space. Conversely, it would not have been necessary to include them if we aimed to select an MDF formulation.
design_space = DesignSpace()
design_space.add_variable("x", lower_bound=0.0, upper_bound=10.0, value=ones(1))
design_space.add_variable(
"z", 2, lower_bound=(-10, 0.0), upper_bound=(10.0, 10.0), value=array([4.0, 3.0])
)
design_space.add_variable("y_1", lower_bound=-100.0, upper_bound=100.0, value=ones(1))
design_space.add_variable("y_2", lower_bound=-100.0, upper_bound=100.0, value=ones(1))
Create the scenario#
In this section, we build the MDO scenario which links the disciplines with the formulation, the design space and the objective function.
scenario = create_scenario(disciplines, "obj", design_space, formulation_name="IDF")
Add the constraints#
Then, we have to set the design constraints
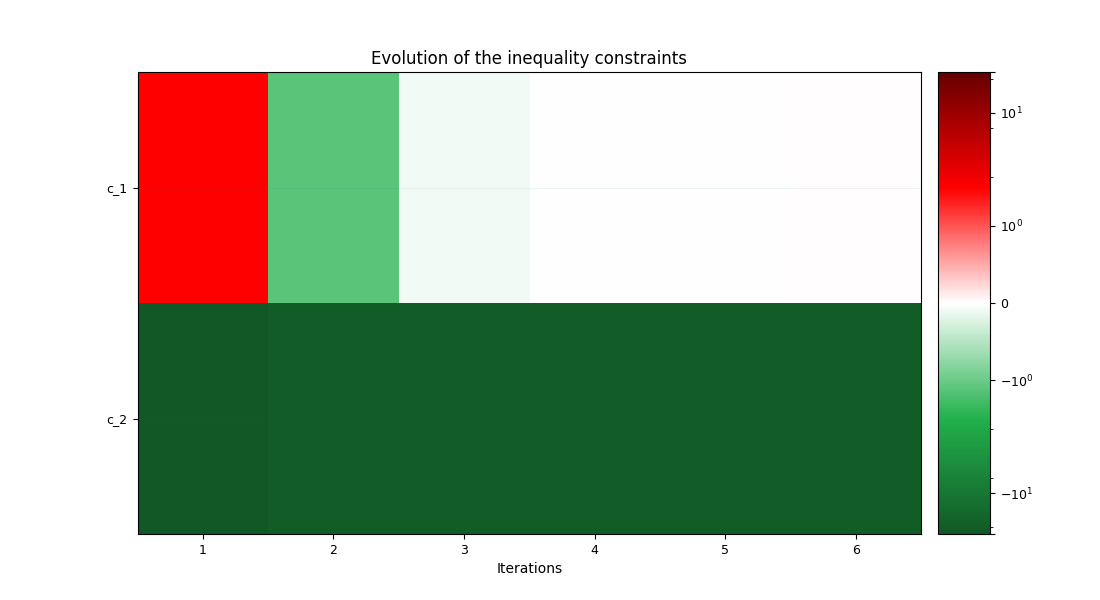
scenario.add_constraint("c_1", constraint_type="ineq")
scenario.add_constraint("c_2", constraint_type="ineq")
As previously mentioned, we are going to use finite differences to approximate the derivatives since the disciplines do not provide them.
scenario.set_differentiation_method("finite_differences")
Execute the scenario#
Then, we execute the MDO scenario with the inputs of the MDO scenario as a dictionary. In this example, the gradient-based SLSQP optimizer is selected, with 10 iterations at maximum:
scenario.execute(algo_name="SLSQP", max_iter=10)
INFO - 08:36:24:
INFO - 08:36:24: *** Start MDOScenario execution ***
INFO - 08:36:24: MDOScenario
INFO - 08:36:24: Disciplines: Sellar1 Sellar2 SellarSystem
INFO - 08:36:24: MDO formulation: IDF
INFO - 08:36:24: Optimization problem:
INFO - 08:36:24: minimize obj(x, z, y_1, y_2)
INFO - 08:36:24: with respect to x, y_1, y_2, z
INFO - 08:36:24: subject to constraints:
INFO - 08:36:24: c_1(x, z, y_1, y_2) <= 0
INFO - 08:36:24: c_2(x, z, y_1, y_2) <= 0
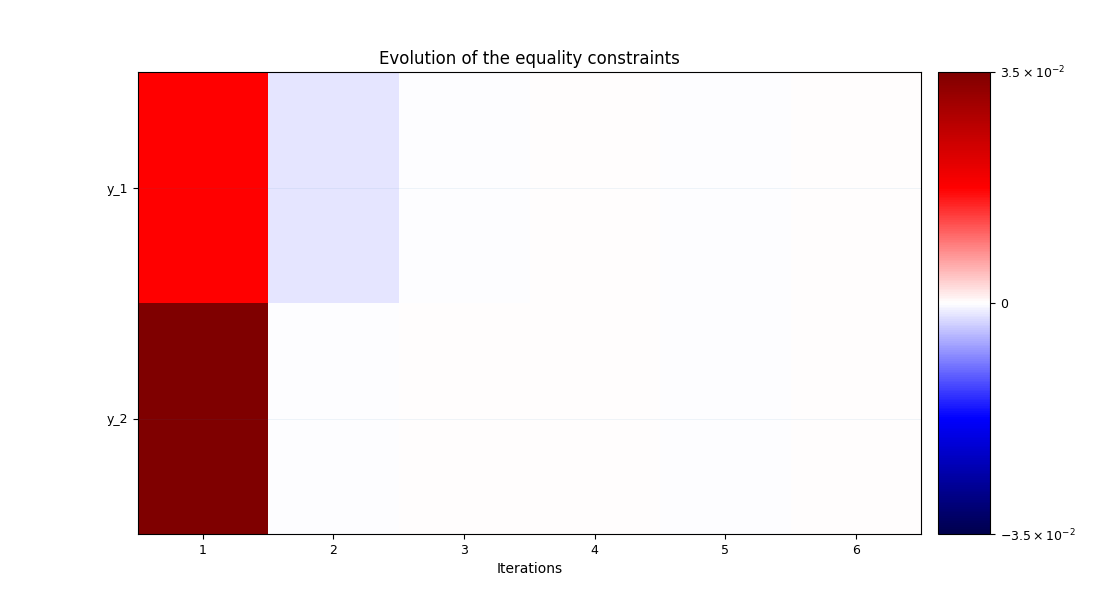
INFO - 08:36:24: y_1(x, z, y_2): y_1(x, z, y_2) - y_1 == 0.0
INFO - 08:36:24: y_2(z, y_1): y_2(z, y_1) - y_2 == 0.0
INFO - 08:36:24: over the design space:
INFO - 08:36:24: +------+-------------+-------+-------------+-------+
INFO - 08:36:24: | Name | Lower bound | Value | Upper bound | Type |
INFO - 08:36:24: +------+-------------+-------+-------------+-------+
INFO - 08:36:24: | x | 0 | 1 | 10 | float |
INFO - 08:36:24: | z[0] | -10 | 4 | 10 | float |
INFO - 08:36:24: | z[1] | 0 | 3 | 10 | float |
INFO - 08:36:24: | y_1 | -100 | 1 | 100 | float |
INFO - 08:36:24: | y_2 | -100 | 1 | 100 | float |
INFO - 08:36:24: +------+-------------+-------+-------------+-------+
INFO - 08:36:24: Solving optimization problem with algorithm SLSQP:
INFO - 08:36:24: 10%|█ | 1/10 [00:00<00:00, 261.00 it/sec, obj=5.37]
INFO - 08:36:24: 20%|██ | 2/10 [00:00<00:00, 108.41 it/sec, obj=4.34]
INFO - 08:36:24: 30%|███ | 3/10 [00:00<00:00, 109.61 it/sec, obj=3.26]
INFO - 08:36:24: 40%|████ | 4/10 [00:00<00:00, 108.71 it/sec, obj=3.18]
INFO - 08:36:24: 50%|█████ | 5/10 [00:00<00:00, 108.31 it/sec, obj=3.18]
INFO - 08:36:24: 60%|██████ | 6/10 [00:00<00:00, 107.32 it/sec, obj=3.18]
INFO - 08:36:24: Optimization result:
INFO - 08:36:24: Optimizer info:
INFO - 08:36:24: Status: 8
INFO - 08:36:24: Message: Positive directional derivative for linesearch
INFO - 08:36:24: Number of calls to the objective function by the optimizer: 7
INFO - 08:36:24: Solution:
INFO - 08:36:24: The solution is feasible.
INFO - 08:36:24: Objective: 3.1833939516400456
INFO - 08:36:24: Standardized constraints:
INFO - 08:36:24: c_1 = 5.764277943853813e-13
INFO - 08:36:24: c_2 = -20.244722233074114
INFO - 08:36:24: y_1 = [2.06834549e-15]
INFO - 08:36:24: y_2 = [1.98063788e-15]
INFO - 08:36:24: Design space:
INFO - 08:36:24: +------+-------------+-------------------+-------------+-------+
INFO - 08:36:24: | Name | Lower bound | Value | Upper bound | Type |
INFO - 08:36:24: +------+-------------+-------------------+-------------+-------+
INFO - 08:36:24: | x | 0 | 0 | 10 | float |
INFO - 08:36:24: | z[0] | -10 | 1.977638883463326 | 10 | float |
INFO - 08:36:24: | z[1] | 0 | 0 | 10 | float |
INFO - 08:36:24: | y_1 | -100 | 1.777638883462956 | 100 | float |
INFO - 08:36:24: | y_2 | -100 | 3.755277766925886 | 100 | float |
INFO - 08:36:24: +------+-------------+-------------------+-------------+-------+
INFO - 08:36:24: *** End MDOScenario execution (time: 0:00:00.080522) ***
Post-process the scenario#
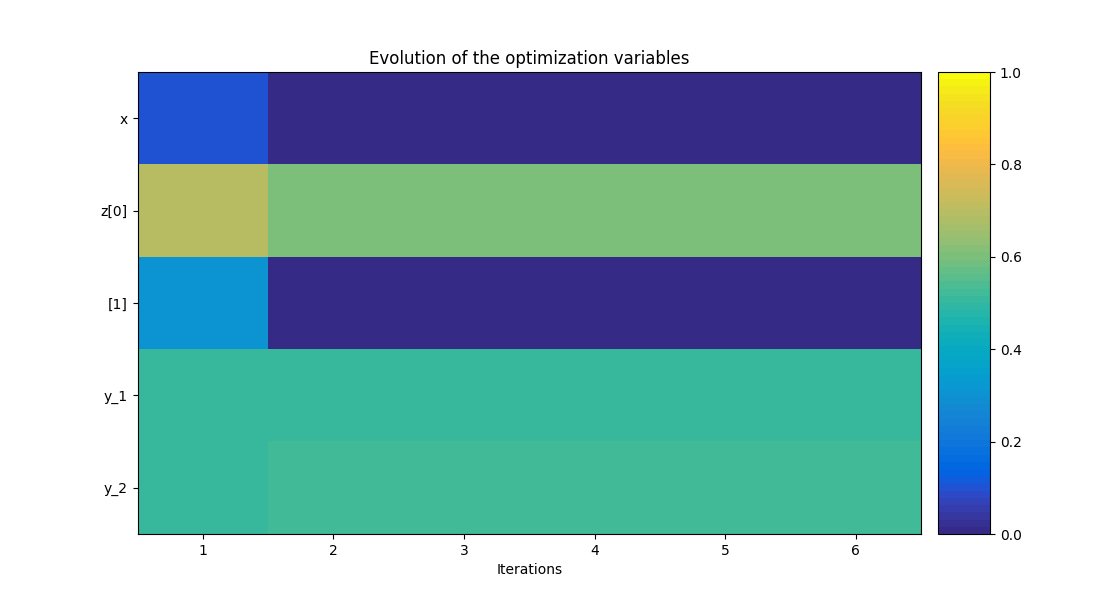
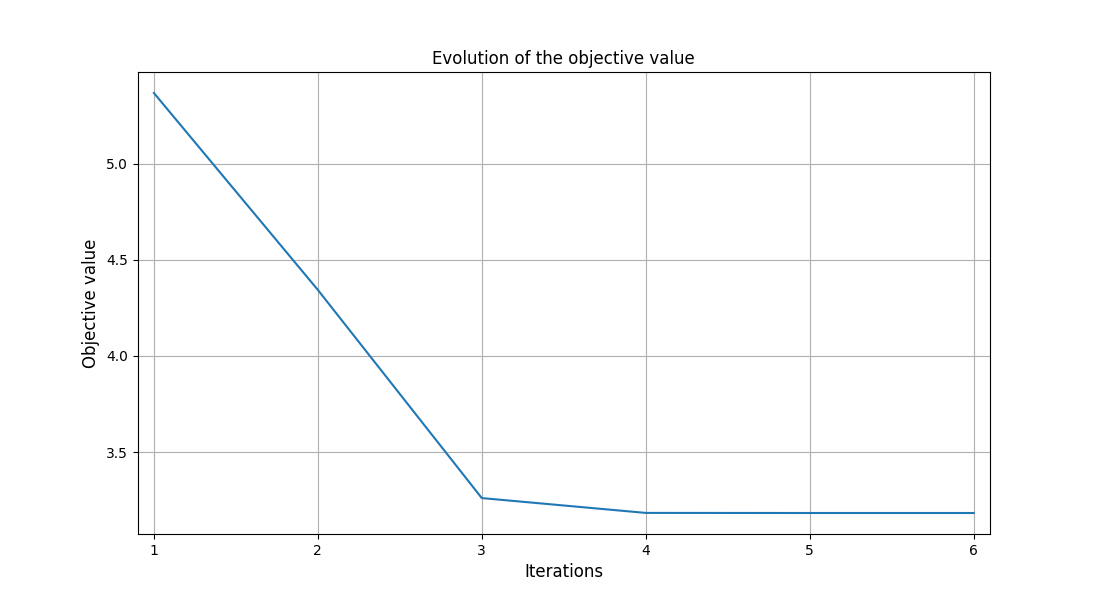
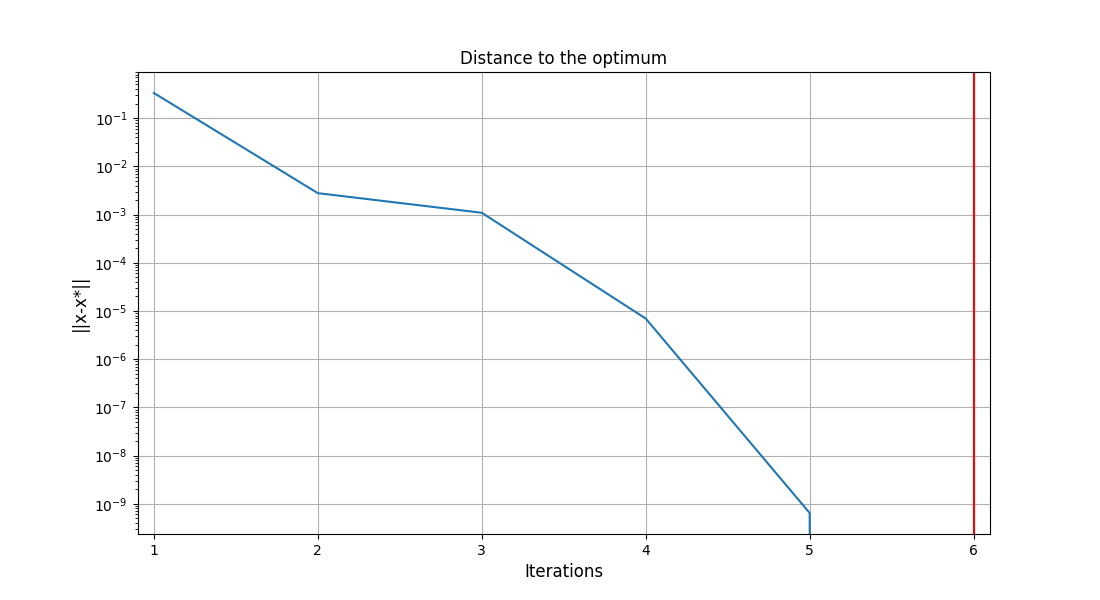
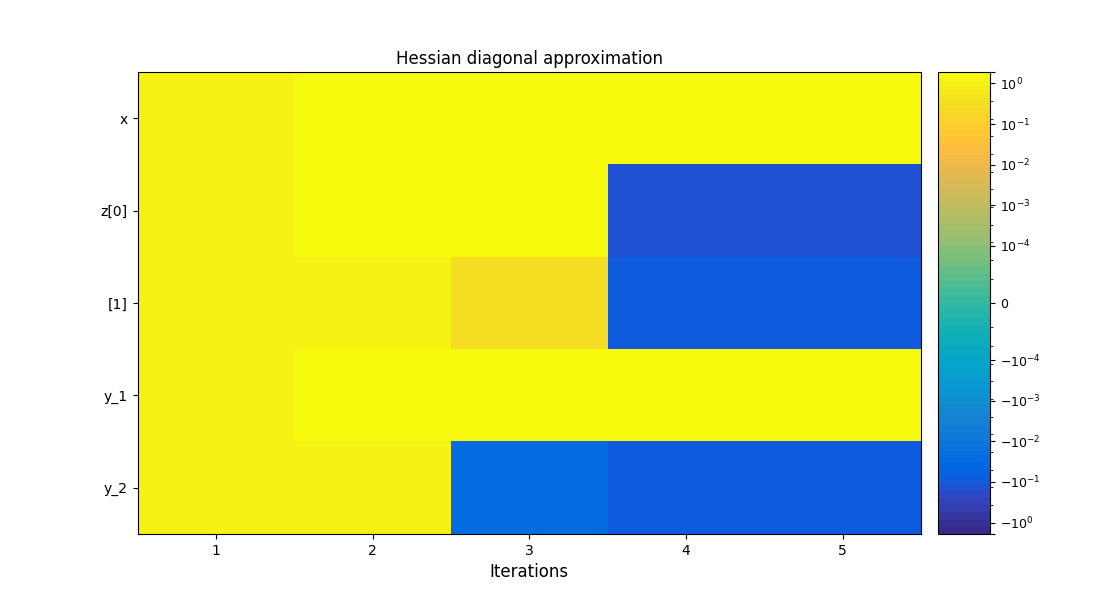
Finally, we can generate plots of the optimization history:
scenario.post_process(post_name="OptHistoryView", save=False, show=True)
<gemseo.post.opt_history_view.OptHistoryView object at 0x7f24f4325580>
Total running time of the script: (0 minutes 1.587 seconds)