Note
Go to the end to download the full example code
PCA on Burgers equation¶
Example using PCA on solutions of the Burgers equation.
from __future__ import annotations
import matplotlib.pyplot as plt
from numpy import eye
from gemseo import configure_logger
from gemseo.mlearning.transformers.dimension_reduction.pca import PCA
from gemseo.problems.dataset.burgers import create_burgers_dataset
configure_logger()
<RootLogger root (INFO)>
Load dataset¶
dataset = create_burgers_dataset(n_samples=20)
dataset
t = dataset.input_dataset.to_numpy()[:, 0]
u_t = dataset.output_dataset.to_numpy()
t_split = 0.87
Plot dataset¶
def lines_gen():
"""Linestyle generator."""
yield "-"
for i in range(1, dataset.n_samples):
yield 0, (i, 1, 1, 1)
color = "red"
lines = lines_gen()
for i in range(dataset.n_samples):
# Switch mode if discontinuity is gone
if color == "red" and t[i] > t_split:
color = "blue"
lines = lines_gen() # reset linestyle generator
plt.plot(u_t[i], color=color, linestyle=next(lines), label=f"t={t[i]:.2f}")
plt.legend()
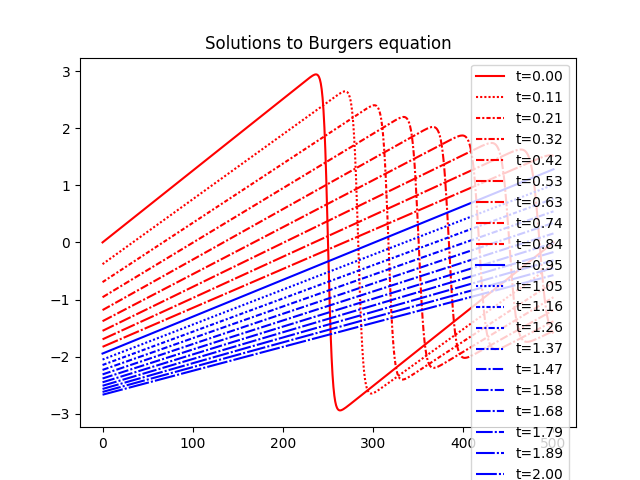
plt.title("Solutions to Burgers equation")
plt.show()
Create PCA¶
n_components = 7
pca = PCA(n_components=n_components)
pca.fit(u_t)
means = u_t.mean(axis=1)
# u_t = u_t - means[:, None]
u_t_reduced = pca.transform(u_t)
u_t_restored = pca.inverse_transform(u_t_reduced)
WARNING - 13:55:27: The Scaler.fit() function does nothing; the instance of Scaler uses the coefficient and offset passed at its initialization
Plot restored data¶
color = "red"
lines = lines_gen()
for i in range(dataset.n_samples):
# Switch mode if discontinuity is gone
if color == "red" and t[i] > t_split:
color = "blue"
lines = lines_gen() # reset linestyle generator
plt.plot(
u_t_restored[i],
color=color, # linestyle=next(lines),
label=f"t={t[i]:.2f}",
)
plt.legend()
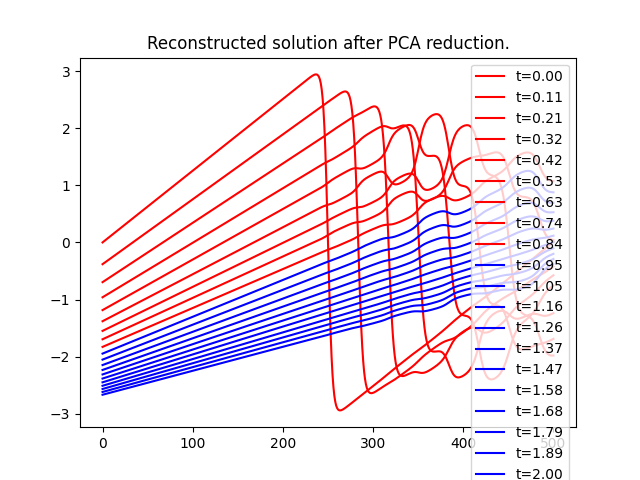
plt.title("Reconstructed solution after PCA reduction.")
plt.show()
Plot principal components¶
red_component = eye(n_components)
components = pca.inverse_transform(red_component)
for i in range(n_components):
plt.plot(components[i])
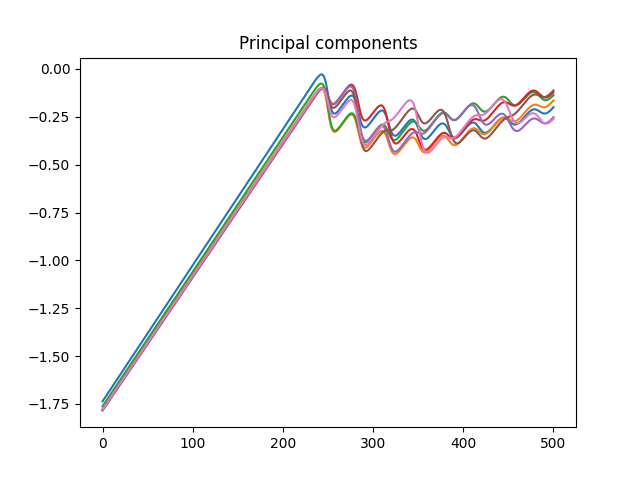
plt.title("Principal components")
plt.show()
Total running time of the script: (0 minutes 0.679 seconds)
