Note
Go to the end to download the full example code
Cross-validation¶
from matplotlib import pyplot as plt
from numpy import array
from numpy import linspace
from numpy import newaxis
from numpy import sin
from gemseo.datasets.io_dataset import IODataset
from gemseo.mlearning.quality_measures.rmse_measure import RMSEMeasure
from gemseo.mlearning.regression.polyreg import PolynomialRegressor
Every quality measure can be computed from a learning dataset or a test dataset. The use of a test dataset aims to approximate the quality of the machine learning model over the whole variable space in order to be less dependent on the learning dataset and so to avoid over-fitting (accurate near learning points and poor elsewhere).
In the presence of expensive data, this test dataset may just be a dream, and we have to estimate this quality with techniques resampling the learning dataset, such as cross-validation. The idea is simple: we divide the learning dataset into \(K\) folds (typically 5), iterate \(K\) times the two-step task “1) learn from \(K-1\) folds, 2) predict from the remainder” and finally approximate the measure from the \(K\) batches of predictions.
To illustrate this point, let us consider the function \(f(x)=(6x-2)^2\sin(12x-4)\) [FSK08]:
def f(x):
return (6 * x - 2) ** 2 * sin(12 * x - 4)
and try to approximate it with a polynomial of order 3.
For this, we can take these 7 learning input points
x_train = array([0.1, 0.3, 0.5, 0.6, 0.8, 0.9, 0.95])
and evaluate the model f over this design of experiments (DOE):
y_train = f(x_train)
Then,
we create an IODataset from these 7 learning samples:
dataset_train = IODataset()
dataset_train.add_input_group(x_train[:, newaxis], ["x"])
dataset_train.add_output_group(y_train[:, newaxis], ["y"])
and build a PolynomialRegressor with degree=3 from it:
polynomial = PolynomialRegressor(dataset_train, 3)
polynomial.learn()
Now, we compute the quality of this model with the RMSE metric:
rmse = RMSEMeasure(polynomial)
rmse.compute_learning_measure()
array([2.37578236])
As the cost of this academic function is zero, we can approximate the generalization quality with a large test dataset whereas the usual test size is about 20% of the training size.
x_test = linspace(0.0, 1.0, 100)
y_test = f(x_test)
dataset_test = IODataset()
dataset_test.add_input_group(x_test[:, newaxis], ["x"])
dataset_test.add_output_group(y_test[:, newaxis], ["y"])
rmse.compute_test_measure(dataset_test)
array([3.31730517])
And do the same by cross-validation with \(K=5\) folds
(this number can be changed with the n_folds arguments):
rmse.compute_cross_validation_measure()
array([14.87187721])
We note that the cross-validation error is pessimistic. As the cross-validation method is based on randomization, we can try again:
rmse.compute_cross_validation_measure()
array([18.9676278])
The result is even more pessimistic. We can take a closer look by storing the sub-models:
rmse.compute_cross_validation_measure(store_resampling_result=True)
array([19.25060777])
and plotting their outputs:
plot = plt.plot(x_test, y_test, label="Reference")
plt.plot(x_train, y_train, "o", color=plot[0].get_color(), label="Training dataset")
plt.plot(x_test, polynomial.predict(x_test[:, newaxis]), label="Model")
for i, algo in enumerate(polynomial.resampling_results["CrossValidation"][1], 1):
plt.plot(x_test, algo.predict(x_test[:, newaxis]), label=f"Sub-model {i}")
plt.legend()
plt.grid()
plt.show()
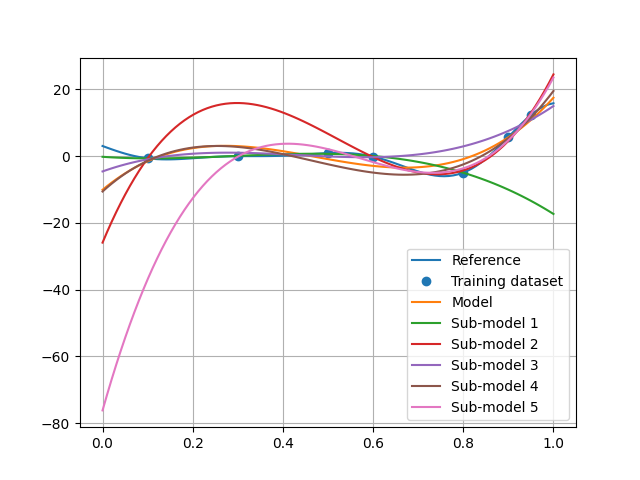
We can see that this pessimistic error is mainly due to the fifth sub-model which did not learn the first training point and therefore has a very high extrapolation error.
Finally, note that we can make the result deterministic by using a custom seed
result = rmse.compute_cross_validation_measure(seed=1)
assert rmse.compute_cross_validation_measure(seed=1) == result
or splitting the samples into \(K\) folds without randomizing them (i.e. first samples in the first fold, next ones in the second, etc.):
result = rmse.compute_cross_validation_measure(randomize=False)
assert rmse.compute_cross_validation_measure(randomize=False) == result
Total running time of the script: (0 minutes 0.326 seconds)
