Note
Go to the end to download the full example code
Analytical test case # 3¶
In this example, we consider a simple optimization problem to illustrate algorithms interfaces and DOE libraries integration. Integer variables are used
Imports¶
from __future__ import annotations
from numpy import sum as np_sum
from gemseo import configure_logger
from gemseo import execute_post
from gemseo.algos.design_space import DesignSpace
from gemseo.algos.doe.doe_factory import DOEFactory
from gemseo.algos.opt_problem import OptimizationProblem
from gemseo.core.mdofunctions.mdo_function import MDOFunction
LOGGER = configure_logger()
Define the objective function¶
We define the objective function \(f(x)=\sum_{i=1}^dx_i\)
using an MDOFunction.
objective = MDOFunction(np_sum, name="f", expr="sum(x)")
Define the design space¶
Then, we define the DesignSpace with GEMSEO.
design_space = DesignSpace()
design_space.add_variable("x", 2, l_b=-5, u_b=5, var_type="integer")
Define the optimization problem¶
Then, we define the OptimizationProblem with GEMSEO.
problem = OptimizationProblem(design_space)
problem.objective = objective
Solve the optimization problem using a DOE algorithm¶
We can see this optimization problem as a trade-off and solve it by means of a design of experiments (DOE), e.g. full factorial design
DOEFactory().execute(problem, "fullfact", n_samples=11**2)
INFO - 13:52:45: Optimization problem:
INFO - 13:52:45: minimize f = sum(x)
INFO - 13:52:45: with respect to x
INFO - 13:52:45: over the design space:
INFO - 13:52:45: +------+-------------+-------+-------------+---------+
INFO - 13:52:45: | Name | Lower bound | Value | Upper bound | Type |
INFO - 13:52:45: +------+-------------+-------+-------------+---------+
INFO - 13:52:45: | x[0] | -5 | None | 5 | integer |
INFO - 13:52:45: | x[1] | -5 | None | 5 | integer |
INFO - 13:52:45: +------+-------------+-------+-------------+---------+
INFO - 13:52:45: Solving optimization problem with algorithm fullfact:
INFO - 13:52:45: 1%| | 1/121 [00:00<00:00, 4136.39 it/sec, obj=-10]
INFO - 13:52:45: 2%|▏ | 2/121 [00:00<00:00, 3316.97 it/sec, obj=-9]
INFO - 13:52:45: 2%|▏ | 3/121 [00:00<00:00, 3263.20 it/sec, obj=-8]
INFO - 13:52:45: 3%|▎ | 4/121 [00:00<00:00, 3270.41 it/sec, obj=-7]
INFO - 13:52:45: 4%|▍ | 5/121 [00:00<00:00, 3285.01 it/sec, obj=-6]
INFO - 13:52:45: 5%|▍ | 6/121 [00:00<00:00, 3292.23 it/sec, obj=-5]
INFO - 13:52:45: 6%|▌ | 7/121 [00:00<00:00, 3303.34 it/sec, obj=-4]
INFO - 13:52:45: 7%|▋ | 8/121 [00:00<00:00, 3308.14 it/sec, obj=-3]
INFO - 13:52:45: 7%|▋ | 9/121 [00:00<00:00, 3312.16 it/sec, obj=-2]
INFO - 13:52:45: 8%|▊ | 10/121 [00:00<00:00, 3318.54 it/sec, obj=-1]
INFO - 13:52:45: 9%|▉ | 11/121 [00:00<00:00, 3324.02 it/sec, obj=0]
INFO - 13:52:45: 10%|▉ | 12/121 [00:00<00:00, 3327.05 it/sec, obj=-9]
INFO - 13:52:45: 11%|█ | 13/121 [00:00<00:00, 3303.40 it/sec, obj=-8]
INFO - 13:52:45: 12%|█▏ | 14/121 [00:00<00:00, 3281.01 it/sec, obj=-7]
INFO - 13:52:45: 12%|█▏ | 15/121 [00:00<00:00, 3284.16 it/sec, obj=-6]
INFO - 13:52:45: 13%|█▎ | 16/121 [00:00<00:00, 3288.68 it/sec, obj=-5]
INFO - 13:52:45: 14%|█▍ | 17/121 [00:00<00:00, 3294.21 it/sec, obj=-4]
INFO - 13:52:45: 15%|█▍ | 18/121 [00:00<00:00, 3299.14 it/sec, obj=-3]
INFO - 13:52:45: 16%|█▌ | 19/121 [00:00<00:00, 3304.66 it/sec, obj=-2]
INFO - 13:52:45: 17%|█▋ | 20/121 [00:00<00:00, 3308.99 it/sec, obj=-1]
INFO - 13:52:45: 17%|█▋ | 21/121 [00:00<00:00, 3312.66 it/sec, obj=0]
INFO - 13:52:45: 18%|█▊ | 22/121 [00:00<00:00, 3316.37 it/sec, obj=1]
INFO - 13:52:45: 19%|█▉ | 23/121 [00:00<00:00, 3319.19 it/sec, obj=-8]
INFO - 13:52:45: 20%|█▉ | 24/121 [00:00<00:00, 3321.89 it/sec, obj=-7]
INFO - 13:52:45: 21%|██ | 25/121 [00:00<00:00, 3323.01 it/sec, obj=-6]
INFO - 13:52:45: 21%|██▏ | 26/121 [00:00<00:00, 3325.36 it/sec, obj=-5]
INFO - 13:52:45: 22%|██▏ | 27/121 [00:00<00:00, 3291.95 it/sec, obj=-4]
INFO - 13:52:45: 23%|██▎ | 28/121 [00:00<00:00, 3291.13 it/sec, obj=-3]
INFO - 13:52:45: 24%|██▍ | 29/121 [00:00<00:00, 3292.95 it/sec, obj=-2]
INFO - 13:52:45: 25%|██▍ | 30/121 [00:00<00:00, 3282.27 it/sec, obj=-1]
INFO - 13:52:45: 26%|██▌ | 31/121 [00:00<00:00, 3275.73 it/sec, obj=0]
INFO - 13:52:45: 26%|██▋ | 32/121 [00:00<00:00, 3274.64 it/sec, obj=1]
INFO - 13:52:45: 27%|██▋ | 33/121 [00:00<00:00, 3264.20 it/sec, obj=2]
INFO - 13:52:45: 28%|██▊ | 34/121 [00:00<00:00, 3259.35 it/sec, obj=-7]
INFO - 13:52:45: 29%|██▉ | 35/121 [00:00<00:00, 3260.35 it/sec, obj=-6]
INFO - 13:52:45: 30%|██▉ | 36/121 [00:00<00:00, 3262.22 it/sec, obj=-5]
INFO - 13:52:45: 31%|███ | 37/121 [00:00<00:00, 3264.87 it/sec, obj=-4]
INFO - 13:52:45: 31%|███▏ | 38/121 [00:00<00:00, 3266.86 it/sec, obj=-3]
INFO - 13:52:45: 32%|███▏ | 39/121 [00:00<00:00, 3257.55 it/sec, obj=-2]
INFO - 13:52:45: 33%|███▎ | 40/121 [00:00<00:00, 3255.06 it/sec, obj=-1]
INFO - 13:52:45: 34%|███▍ | 41/121 [00:00<00:00, 3257.00 it/sec, obj=0]
INFO - 13:52:45: 35%|███▍ | 42/121 [00:00<00:00, 3258.92 it/sec, obj=1]
INFO - 13:52:45: 36%|███▌ | 43/121 [00:00<00:00, 3260.33 it/sec, obj=2]
INFO - 13:52:45: 36%|███▋ | 44/121 [00:00<00:00, 3262.49 it/sec, obj=3]
INFO - 13:52:45: 37%|███▋ | 45/121 [00:00<00:00, 3264.78 it/sec, obj=-6]
INFO - 13:52:45: 38%|███▊ | 46/121 [00:00<00:00, 3267.09 it/sec, obj=-5]
INFO - 13:52:45: 39%|███▉ | 47/121 [00:00<00:00, 3268.65 it/sec, obj=-4]
INFO - 13:52:45: 40%|███▉ | 48/121 [00:00<00:00, 3270.41 it/sec, obj=-3]
INFO - 13:52:45: 40%|████ | 49/121 [00:00<00:00, 3272.47 it/sec, obj=-2]
INFO - 13:52:45: 41%|████▏ | 50/121 [00:00<00:00, 3273.88 it/sec, obj=-1]
INFO - 13:52:45: 42%|████▏ | 51/121 [00:00<00:00, 3275.80 it/sec, obj=0]
INFO - 13:52:45: 43%|████▎ | 52/121 [00:00<00:00, 3277.54 it/sec, obj=1]
INFO - 13:52:45: 44%|████▍ | 53/121 [00:00<00:00, 3267.89 it/sec, obj=2]
INFO - 13:52:45: 45%|████▍ | 54/121 [00:00<00:00, 3268.90 it/sec, obj=3]
INFO - 13:52:45: 45%|████▌ | 55/121 [00:00<00:00, 3269.97 it/sec, obj=4]
INFO - 13:52:45: 46%|████▋ | 56/121 [00:00<00:00, 3271.60 it/sec, obj=-5]
INFO - 13:52:45: 47%|████▋ | 57/121 [00:00<00:00, 3272.67 it/sec, obj=-4]
INFO - 13:52:45: 48%|████▊ | 58/121 [00:00<00:00, 3274.20 it/sec, obj=-3]
INFO - 13:52:45: 49%|████▉ | 59/121 [00:00<00:00, 3275.63 it/sec, obj=-2]
INFO - 13:52:45: 50%|████▉ | 60/121 [00:00<00:00, 3276.54 it/sec, obj=-1]
INFO - 13:52:45: 50%|█████ | 61/121 [00:00<00:00, 3277.85 it/sec, obj=0]
INFO - 13:52:45: 51%|█████ | 62/121 [00:00<00:00, 3279.16 it/sec, obj=1]
INFO - 13:52:45: 52%|█████▏ | 63/121 [00:00<00:00, 3280.42 it/sec, obj=2]
INFO - 13:52:45: 53%|█████▎ | 64/121 [00:00<00:00, 3277.36 it/sec, obj=3]
INFO - 13:52:45: 54%|█████▎ | 65/121 [00:00<00:00, 3276.41 it/sec, obj=4]
INFO - 13:52:45: 55%|█████▍ | 66/121 [00:00<00:00, 3269.52 it/sec, obj=5]
INFO - 13:52:45: 55%|█████▌ | 67/121 [00:00<00:00, 3269.25 it/sec, obj=-4]
INFO - 13:52:45: 56%|█████▌ | 68/121 [00:00<00:00, 3270.26 it/sec, obj=-3]
INFO - 13:52:45: 57%|█████▋ | 69/121 [00:00<00:00, 3271.61 it/sec, obj=-2]
INFO - 13:52:45: 58%|█████▊ | 70/121 [00:00<00:00, 3272.60 it/sec, obj=-1]
INFO - 13:52:45: 59%|█████▊ | 71/121 [00:00<00:00, 3273.81 it/sec, obj=0]
INFO - 13:52:45: 60%|█████▉ | 72/121 [00:00<00:00, 3274.67 it/sec, obj=1]
INFO - 13:52:45: 60%|██████ | 73/121 [00:00<00:00, 3275.89 it/sec, obj=2]
INFO - 13:52:45: 61%|██████ | 74/121 [00:00<00:00, 3277.22 it/sec, obj=3]
INFO - 13:52:45: 62%|██████▏ | 75/121 [00:00<00:00, 3278.13 it/sec, obj=4]
INFO - 13:52:45: 63%|██████▎ | 76/121 [00:00<00:00, 3279.19 it/sec, obj=5]
INFO - 13:52:45: 64%|██████▎ | 77/121 [00:00<00:00, 3280.23 it/sec, obj=6]
INFO - 13:52:45: 64%|██████▍ | 78/121 [00:00<00:00, 3281.53 it/sec, obj=-3]
INFO - 13:52:45: 65%|██████▌ | 79/121 [00:00<00:00, 3276.05 it/sec, obj=-2]
INFO - 13:52:45: 66%|██████▌ | 80/121 [00:00<00:00, 3276.19 it/sec, obj=-1]
INFO - 13:52:45: 67%|██████▋ | 81/121 [00:00<00:00, 3277.18 it/sec, obj=0]
INFO - 13:52:45: 68%|██████▊ | 82/121 [00:00<00:00, 3278.27 it/sec, obj=1]
INFO - 13:52:45: 69%|██████▊ | 83/121 [00:00<00:00, 3279.45 it/sec, obj=2]
INFO - 13:52:45: 69%|██████▉ | 84/121 [00:00<00:00, 3280.74 it/sec, obj=3]
INFO - 13:52:45: 70%|███████ | 85/121 [00:00<00:00, 3281.69 it/sec, obj=4]
INFO - 13:52:45: 71%|███████ | 86/121 [00:00<00:00, 3260.95 it/sec, obj=5]
INFO - 13:52:45: 72%|███████▏ | 87/121 [00:00<00:00, 3260.46 it/sec, obj=6]
INFO - 13:52:45: 73%|███████▎ | 88/121 [00:00<00:00, 3261.22 it/sec, obj=7]
INFO - 13:52:45: 74%|███████▎ | 89/121 [00:00<00:00, 3262.40 it/sec, obj=-2]
INFO - 13:52:45: 74%|███████▍ | 90/121 [00:00<00:00, 3263.29 it/sec, obj=-1]
INFO - 13:52:45: 75%|███████▌ | 91/121 [00:00<00:00, 3264.61 it/sec, obj=0]
INFO - 13:52:45: 76%|███████▌ | 92/121 [00:00<00:00, 3259.58 it/sec, obj=1]
INFO - 13:52:45: 77%|███████▋ | 93/121 [00:00<00:00, 3260.15 it/sec, obj=2]
INFO - 13:52:45: 78%|███████▊ | 94/121 [00:00<00:00, 3261.05 it/sec, obj=3]
INFO - 13:52:45: 79%|███████▊ | 95/121 [00:00<00:00, 3261.91 it/sec, obj=4]
INFO - 13:52:45: 79%|███████▉ | 96/121 [00:00<00:00, 3263.20 it/sec, obj=5]
INFO - 13:52:45: 80%|████████ | 97/121 [00:00<00:00, 3264.18 it/sec, obj=6]
INFO - 13:52:45: 81%|████████ | 98/121 [00:00<00:00, 3265.14 it/sec, obj=7]
INFO - 13:52:45: 82%|████████▏ | 99/121 [00:00<00:00, 3266.21 it/sec, obj=8]
INFO - 13:52:45: 83%|████████▎ | 100/121 [00:00<00:00, 3262.27 it/sec, obj=-1]
INFO - 13:52:45: 83%|████████▎ | 101/121 [00:00<00:00, 3261.29 it/sec, obj=0]
INFO - 13:52:45: 84%|████████▍ | 102/121 [00:00<00:00, 3261.74 it/sec, obj=1]
INFO - 13:52:45: 85%|████████▌ | 103/121 [00:00<00:00, 3262.47 it/sec, obj=2]
INFO - 13:52:45: 86%|████████▌ | 104/121 [00:00<00:00, 3263.12 it/sec, obj=3]
INFO - 13:52:45: 87%|████████▋ | 105/121 [00:00<00:00, 3258.78 it/sec, obj=4]
INFO - 13:52:45: 88%|████████▊ | 106/121 [00:00<00:00, 3259.17 it/sec, obj=5]
INFO - 13:52:45: 88%|████████▊ | 107/121 [00:00<00:00, 3259.92 it/sec, obj=6]
INFO - 13:52:45: 89%|████████▉ | 108/121 [00:00<00:00, 3260.97 it/sec, obj=7]
INFO - 13:52:45: 90%|█████████ | 109/121 [00:00<00:00, 3261.74 it/sec, obj=8]
INFO - 13:52:45: 91%|█████████ | 110/121 [00:00<00:00, 3262.80 it/sec, obj=9]
INFO - 13:52:45: 92%|█████████▏| 111/121 [00:00<00:00, 3263.87 it/sec, obj=0]
INFO - 13:52:45: 93%|█████████▎| 112/121 [00:00<00:00, 3264.82 it/sec, obj=1]
INFO - 13:52:45: 93%|█████████▎| 113/121 [00:00<00:00, 3265.83 it/sec, obj=2]
INFO - 13:52:45: 94%|█████████▍| 114/121 [00:00<00:00, 3266.88 it/sec, obj=3]
INFO - 13:52:45: 95%|█████████▌| 115/121 [00:00<00:00, 3267.81 it/sec, obj=4]
INFO - 13:52:45: 96%|█████████▌| 116/121 [00:00<00:00, 3268.74 it/sec, obj=5]
INFO - 13:52:45: 97%|█████████▋| 117/121 [00:00<00:00, 3269.75 it/sec, obj=6]
INFO - 13:52:45: 98%|█████████▊| 118/121 [00:00<00:00, 3266.53 it/sec, obj=7]
INFO - 13:52:45: 98%|█████████▊| 119/121 [00:00<00:00, 3266.53 it/sec, obj=8]
INFO - 13:52:45: 99%|█████████▉| 120/121 [00:00<00:00, 3267.38 it/sec, obj=9]
INFO - 13:52:45: 100%|██████████| 121/121 [00:00<00:00, 3268.23 it/sec, obj=10]
INFO - 13:52:45: Optimization result:
INFO - 13:52:45: Optimizer info:
INFO - 13:52:45: Status: None
INFO - 13:52:45: Message: None
INFO - 13:52:45: Number of calls to the objective function by the optimizer: 121
INFO - 13:52:45: Solution:
INFO - 13:52:45: Objective: -10.0
INFO - 13:52:45: Design space:
INFO - 13:52:45: +------+-------------+-------+-------------+---------+
INFO - 13:52:45: | Name | Lower bound | Value | Upper bound | Type |
INFO - 13:52:45: +------+-------------+-------+-------------+---------+
INFO - 13:52:45: | x[0] | -5 | -5 | 5 | integer |
INFO - 13:52:45: | x[1] | -5 | -5 | 5 | integer |
INFO - 13:52:45: +------+-------------+-------+-------------+---------+
Post-process the results¶
execute_post(
problem,
"ScatterPlotMatrix",
variable_names=["x", "f"],
save=False,
show=True,
)
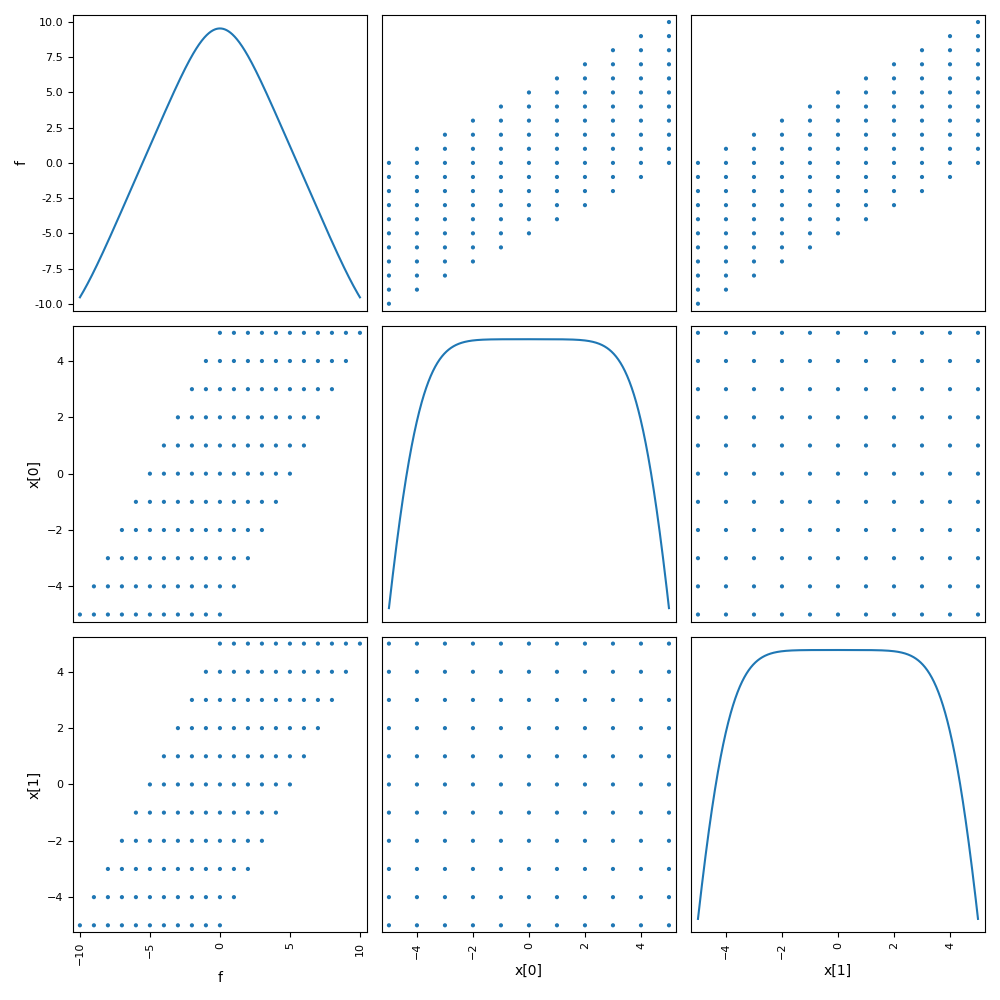
<gemseo.post.scatter_mat.ScatterPlotMatrix object at 0x7f2d3f331820>
Note that you can get all the optimization algorithms names:
DOEFactory().algorithms
['CustomDOE', 'DiagonalDOE', 'OT_SOBOL', 'OT_RANDOM', 'OT_HASELGROVE', 'OT_REVERSE_HALTON', 'OT_HALTON', 'OT_FAURE', 'OT_MONTE_CARLO', 'OT_FACTORIAL', 'OT_COMPOSITE', 'OT_AXIAL', 'OT_OPT_LHS', 'OT_LHS', 'OT_LHSC', 'OT_FULLFACT', 'OT_SOBOL_INDICES', 'fullfact', 'ff2n', 'pbdesign', 'bbdesign', 'ccdesign', 'lhs', 'Halton', 'LHS', 'MC', 'PoissonDisk', 'Sobol']
Total running time of the script: (0 minutes 0.725 seconds)
