Note

Go to the end to download the full example code

Analytical test case # 2

In this example, we consider a simple optimization problem to illustrate algorithms interfaces and optimization libraries integration.

Imports

from __future__ import annotations

from numpy import cos
from numpy import exp
from numpy import ones
from numpy import sin

from gemseo import configure_logger
from gemseo import execute_post
from gemseo.algos.design_space import DesignSpace
from gemseo.algos.doe.doe_factory import DOEFactory
from gemseo.algos.opt.opt_factory import OptimizersFactory
from gemseo.algos.opt_problem import OptimizationProblem
from gemseo.core.mdofunctions.mdo_function import MDOFunction

configure_logger()

<RootLogger root (INFO)>

Define the objective function

We define the objective function \(f(x)=\sin(x)-\exp(x)\) using an MDOFunction defined by the sum of MDOFunction objects.

f_1 = MDOFunction(sin, name="f_1", jac=cos, expr="sin(x)")
f_2 = MDOFunction(exp, name="f_2", jac=exp, expr="exp(x)")
objective = f_1 - f_2

See also

The following operators are implemented: addition, subtraction and multiplication. The minus operator is also defined.

Define the design space

Then, we define the DesignSpace with GEMSEO.

design_space = DesignSpace()
design_space.add_variable("x", l_b=-2.0, u_b=2.0, value=-0.5 * ones(1))

Define the optimization problem

Then, we define the OptimizationProblem with GEMSEO.

problem = OptimizationProblem(design_space)
problem.objective = objective

Solve the optimization problem using an optimization algorithm

Finally, we solve the optimization problems with GEMSEO interface.

Solve the problem

opt = OptimizersFactory().execute(problem, "L-BFGS-B", normalize_design_space=True)
opt

INFO - 13:07:12: Optimization problem:
INFO - 13:07:12:    minimize [f_1-f_2] = sin(x)-exp(x)
INFO - 13:07:12:    with respect to x
INFO - 13:07:12:    over the design space:
INFO - 13:07:12:       +------+-------------+-------+-------------+-------+
INFO - 13:07:12:       | Name | Lower bound | Value | Upper bound | Type  |
INFO - 13:07:12:       +------+-------------+-------+-------------+-------+
INFO - 13:07:12:       | x    |      -2     |  -0.5 |      2      | float |
INFO - 13:07:12:       +------+-------------+-------+-------------+-------+
INFO - 13:07:12: Solving optimization problem with algorithm L-BFGS-B:
INFO - 13:07:12:      1%|          | 5/999 [00:00<00:00, 1178.24 it/sec, obj=-1.24]
INFO - 13:07:12:      1%|          | 6/999 [00:00<00:00, 1122.42 it/sec, obj=-1.24]
INFO - 13:07:12:      1%|          | 7/999 [00:00<00:00, 1093.24 it/sec, obj=-1.24]
INFO - 13:07:12: Optimization result:
INFO - 13:07:12:    Optimizer info:
INFO - 13:07:12:       Status: 0
INFO - 13:07:12:       Message: CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
INFO - 13:07:12:       Number of calls to the objective function by the optimizer: 8
INFO - 13:07:12:    Solution:
INFO - 13:07:12:       Objective: -1.2361083418592416
INFO - 13:07:12:       Design space:
INFO - 13:07:12:          +------+-------------+--------------------+-------------+-------+
INFO - 13:07:12:          | Name | Lower bound |       Value        | Upper bound | Type  |
INFO - 13:07:12:          +------+-------------+--------------------+-------------+-------+
INFO - 13:07:12:          | x    |      -2     | -1.292695718944152 |      2      | float |
INFO - 13:07:12:          +------+-------------+--------------------+-------------+-------+
Optimization result:
  • Design variables: [-1.29269572]
  • Objective function: -1.2361083418592416
  • Feasible solution: True


Note that you can get all the optimization algorithms names:

OptimizersFactory().algorithms

['Augmented_Lagrangian_order_0', 'Augmented_Lagrangian_order_1', 'MMA', 'MNBI', 'NLOPT_MMA', 'NLOPT_COBYLA', 'NLOPT_SLSQP', 'NLOPT_BOBYQA', 'NLOPT_BFGS', 'NLOPT_NEWUOA', 'PDFO_COBYLA', 'PDFO_BOBYQA', 'PDFO_NEWUOA', 'PSEVEN', 'PSEVEN_FD', 'PSEVEN_MOM', 'PSEVEN_NCG', 'PSEVEN_NLS', 'PSEVEN_POWELL', 'PSEVEN_QP', 'PSEVEN_SQP', 'PSEVEN_SQ2P', 'PYMOO_GA', 'PYMOO_NSGA2', 'PYMOO_NSGA3', 'PYMOO_UNSGA3', 'PYMOO_RNSGA3', 'DUAL_ANNEALING', 'SHGO', 'DIFFERENTIAL_EVOLUTION', 'LINEAR_INTERIOR_POINT', 'REVISED_SIMPLEX', 'SIMPLEX', 'HIGHS_INTERIOR_POINT', 'HIGHS_DUAL_SIMPLEX', 'HIGHS', 'Scipy_MILP', 'SLSQP', 'L-BFGS-B', 'TNC', 'NELDER-MEAD']

Save the optimization results

We can serialize the results for further exploitation.

problem.to_hdf("my_optim.hdf5")

INFO - 13:07:12: Exporting the optimization problem to the file my_optim.hdf5 at node

Post-process the results

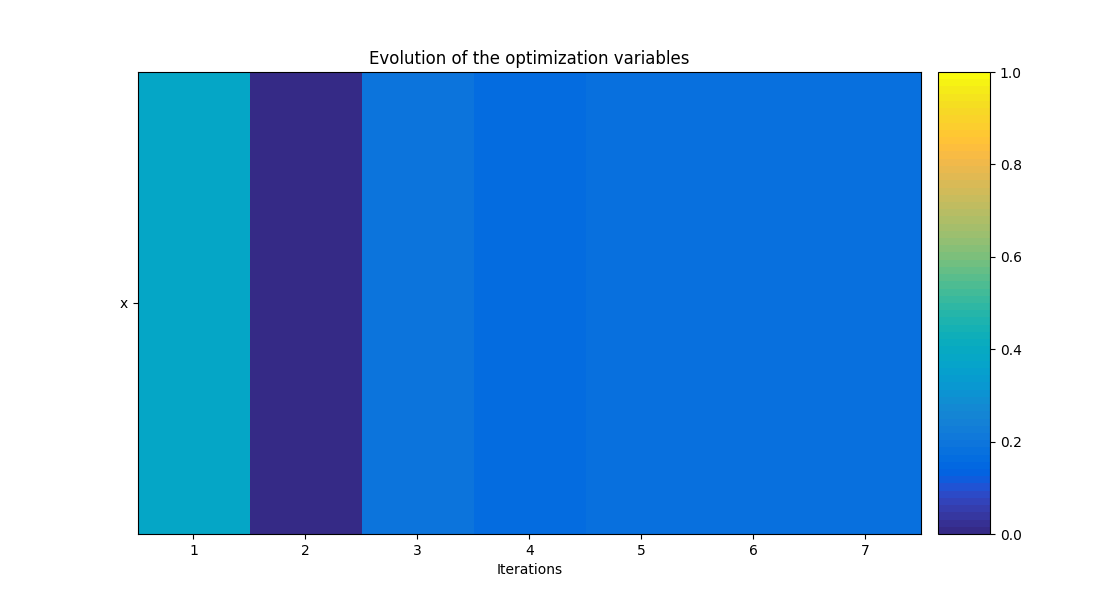
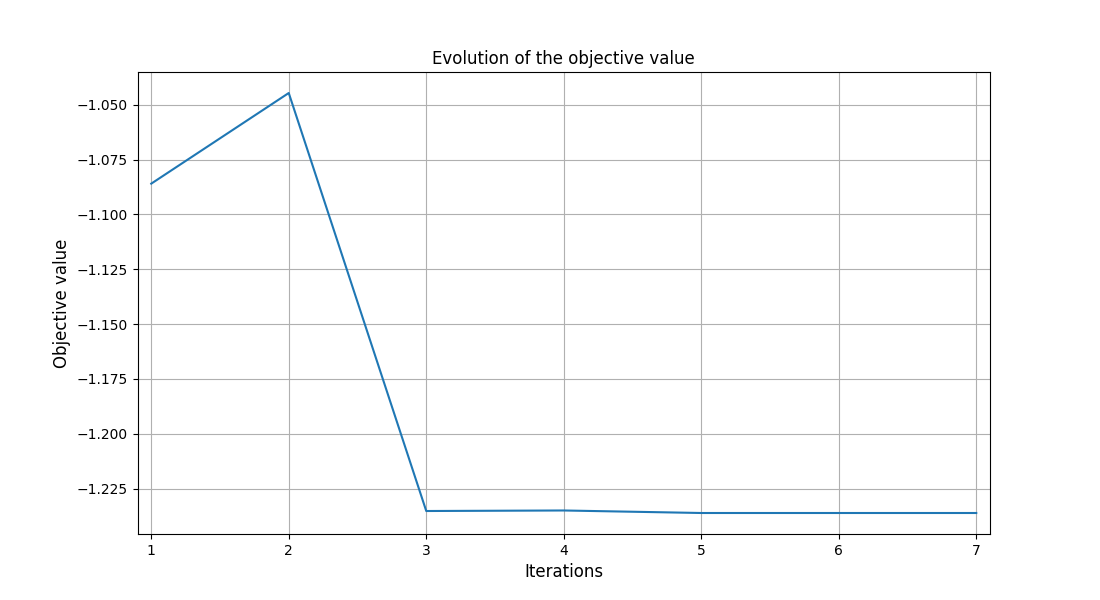
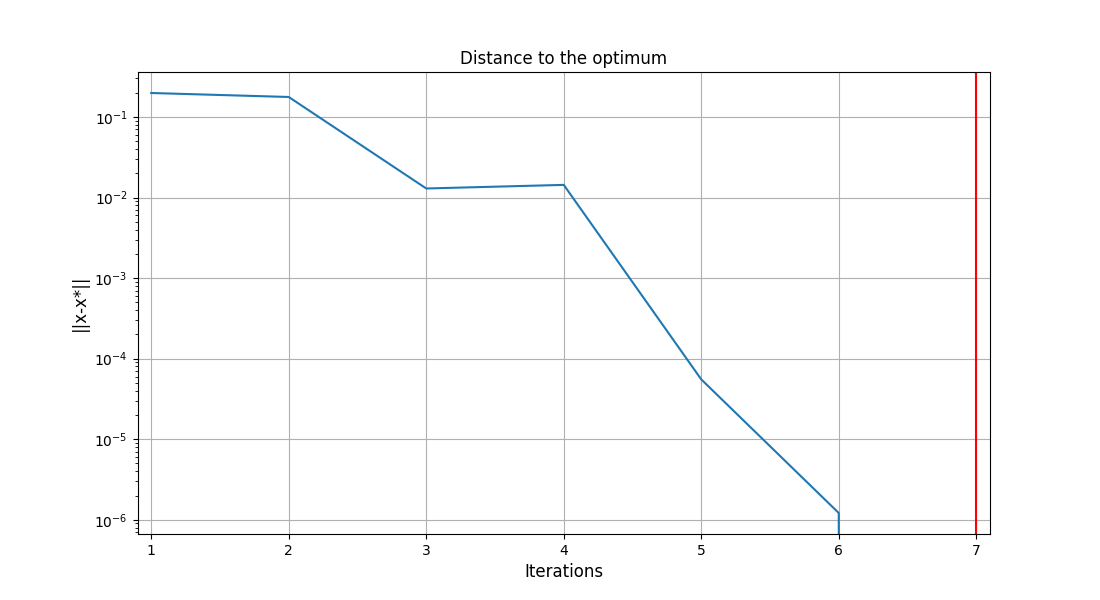
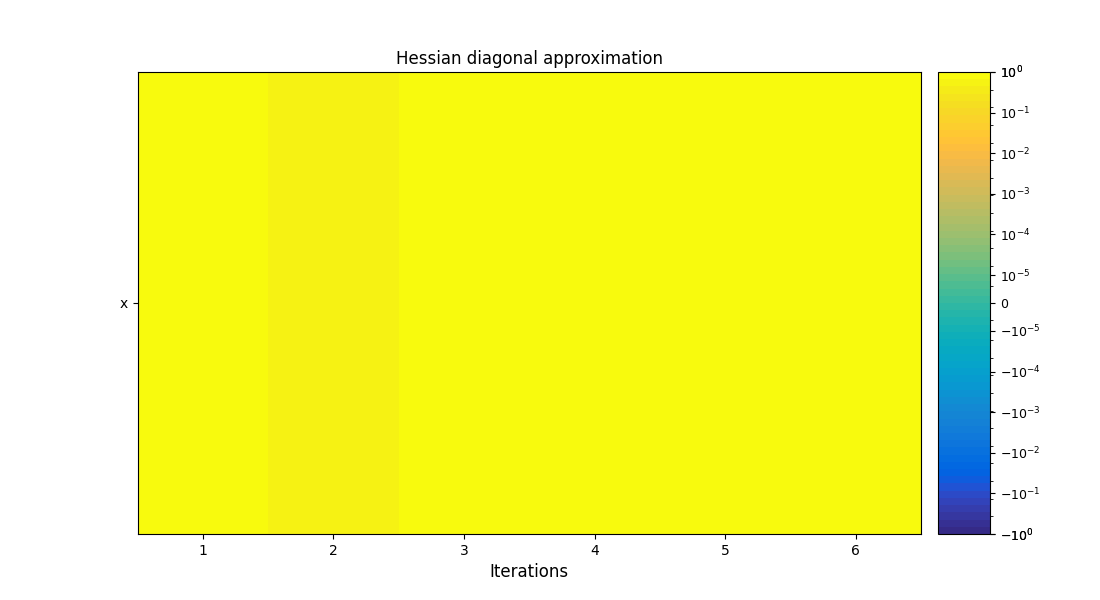
execute_post(problem, "OptHistoryView", show=True, save=False)
  • Evolution of the optimization variables
  • Evolution of the objective value
  • Distance to the optimum
  • Hessian diagonal approximation
<gemseo.post.opt_history_view.OptHistoryView object at 0x7f6b89072d60>

Note

We can also save this plot using the arguments save=False and file_path='file_path'.

Solve the optimization problem using a DOE algorithm

We can also see this optimization problem as a trade-off and solve it by means of a design of experiments (DOE).

opt = DOEFactory().execute(problem, "lhs", n_samples=10, normalize_design_space=True)
opt

INFO - 13:07:13: Optimization problem:
INFO - 13:07:13:    minimize [f_1-f_2] = sin(x)-exp(x)
INFO - 13:07:13:    with respect to x
INFO - 13:07:13:    over the design space:
INFO - 13:07:13:       +------+-------------+--------------------+-------------+-------+
INFO - 13:07:13:       | Name | Lower bound |       Value        | Upper bound | Type  |
INFO - 13:07:13:       +------+-------------+--------------------+-------------+-------+
INFO - 13:07:13:       | x    |      -2     | -1.292695718944152 |      2      | float |
INFO - 13:07:13:       +------+-------------+--------------------+-------------+-------+
INFO - 13:07:13: Solving optimization problem with algorithm lhs:
INFO - 13:07:13:     10%|█         | 1/10 [00:00<00:00, 2571.61 it/sec, obj=-5.17]
INFO - 13:07:13:     20%|██        | 2/10 [00:00<00:00, 2351.73 it/sec, obj=-1.15]
INFO - 13:07:13:     30%|███       | 3/10 [00:00<00:00, 2431.01 it/sec, obj=-1.24]
INFO - 13:07:13:     40%|████      | 4/10 [00:00<00:00, 2468.33 it/sec, obj=-1.13]
INFO - 13:07:13:     50%|█████     | 5/10 [00:00<00:00, 2500.78 it/sec, obj=-2.91]
INFO - 13:07:13:     60%|██████    | 6/10 [00:00<00:00, 2532.03 it/sec, obj=-1.75]
INFO - 13:07:13:     70%|███████   | 7/10 [00:00<00:00, 2557.06 it/sec, obj=-1.14]
INFO - 13:07:13:     80%|████████  | 8/10 [00:00<00:00, 2574.97 it/sec, obj=-1.05]
INFO - 13:07:13:     90%|█████████ | 9/10 [00:00<00:00, 2595.13 it/sec, obj=-1.23]
INFO - 13:07:13:    100%|██████████| 10/10 [00:00<00:00, 2613.27 it/sec, obj=-1]
INFO - 13:07:13: Optimization result:
INFO - 13:07:13:    Optimizer info:
INFO - 13:07:13:       Status: None
INFO - 13:07:13:       Message: None
INFO - 13:07:13:       Number of calls to the objective function by the optimizer: 18
INFO - 13:07:13:    Solution:
INFO - 13:07:13:       Objective: -5.174108803965849
INFO - 13:07:13:       Design space:
INFO - 13:07:13:          +------+-------------+-------------------+-------------+-------+
INFO - 13:07:13:          | Name | Lower bound |       Value       | Upper bound | Type  |
INFO - 13:07:13:          +------+-------------+-------------------+-------------+-------+
INFO - 13:07:13:          | x    |      -2     | 1.815526693601343 |      2      | float |
INFO - 13:07:13:          +------+-------------+-------------------+-------------+-------+
Optimization result:
  • Design variables: [1.81552669]
  • Objective function: -5.174108803965849
  • Feasible solution: True


Total running time of the script: (0 minutes 1.052 seconds)

Gallery generated by Sphinx-Gallery