Note
Click here to download the full example code
Comparing sensitivity indices¶
from __future__ import annotations
from gemseo.algos.parameter_space import ParameterSpace
from gemseo.api import create_discipline
from gemseo.uncertainty.sensitivity.correlation.analysis import CorrelationAnalysis
from gemseo.uncertainty.sensitivity.morris.analysis import MorrisAnalysis
from matplotlib import pyplot as plt
from numpy import pi
In this example, we consider the Ishigami function:
which is well-known in the uncertainty domain:
expressions = {"y": "sin(x1)+7*sin(x2)**2+0.1*x3**4*sin(x1)"}
discipline = create_discipline(
"AnalyticDiscipline", expressions=expressions, name="Ishigami"
)
The different uncertain variables \(X_1\) , \(X_2\) and \(X_3\) are independent and identically distributed according to an uniform distribution between \(-\pi\) and \(\pi\):
space = ParameterSpace()
for variable in ["x1", "x2", "x3"]:
space.add_random_variable(
variable, "OTUniformDistribution", minimum=-pi, maximum=pi
)
We would like to carry out two sensitivity analyses, e.g. a first one based on correlation coefficients and a second one based on the Morris methodology, and compare the results,
Firstly,
we create a CorrelationAnalysis
and compute the sensitivity indices:
correlation = CorrelationAnalysis([discipline], space, 10)
correlation.compute_indices()
{'pearson': {'y': [{'x1': array([0.685388]), 'x2': array([0.09681897]), 'x3': array([-0.23027298])}]}, 'spearman': {'y': [{'x1': array([0.74545455]), 'x2': array([0.04242424]), 'x3': array([-0.09090909])}]}, 'pcc': {'y': [{'x1': array([0.84696461]), 'x2': array([0.68814608]), 'x3': array([-0.29846394])}]}, 'prcc': {'y': [{'x1': array([0.90374102]), 'x2': array([0.76539572]), 'x3': array([-0.02232206])}]}, 'src': {'y': [{'x1': array([0.88362459]), 'x2': array([0.31079367]), 'x3': array([0.0261049])}]}, 'srrc': {'y': [{'x1': array([1.12896579]), 'x2': array([0.36201552]), 'x3': array([9.21486583e-05])}]}, 'ssrrc': {'y': [{'x1': array([0.94001308]), 'x2': array([0.55748872]), 'x3': array([-0.16157012])}]}}
Then,
we create a MorrisAnalysis
and compute the sensitivity indices:
morris = MorrisAnalysis([discipline], space, 10)
morris.compute_indices()
{'mu': {'y': [{'x1': array([-0.36000398]), 'x2': array([0.77781853]), 'x3': array([-0.70990541])}]}, 'mu_star': {'y': [{'x1': array([0.67947346]), 'x2': array([0.88906579]), 'x3': array([0.72694219])}]}, 'sigma': {'y': [{'x1': array([0.98724949]), 'x2': array([0.79064599]), 'x3': array([0.8074493])}]}, 'relative_sigma': {'y': [{'x1': array([1.45296254]), 'x2': array([0.88929976]), 'x3': array([1.11074761])}]}, 'min': {'y': [{'x1': array([0.0338188]), 'x2': array([0.11821721]), 'x3': array([8.72820113e-05])}]}, 'max': {'y': [{'x1': array([2.2360336]), 'x2': array([1.83987522]), 'x3': array([2.12052546])}]}}
Lastly,
we compare these analyses
with the graphical method SensitivityAnalysis.plot_comparison(),
either using a bar chart:
morris.plot_comparison(correlation, "y", use_bar_plot=True, save=False, show=False)
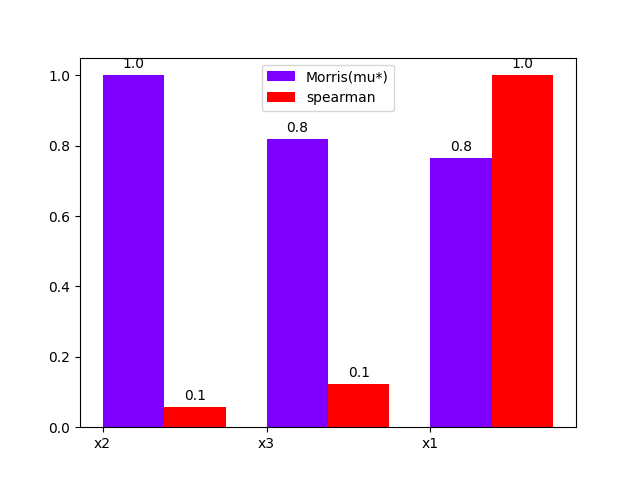
<gemseo.post.dataset.bars.BarPlot object at 0x7f3bf999dfd0>
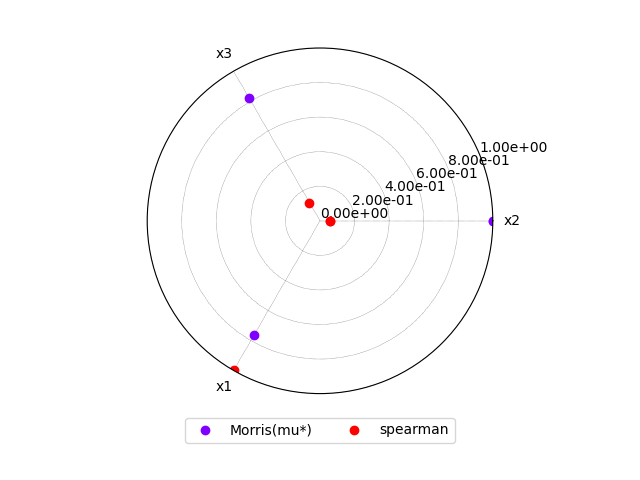
or a radar plot:
morris.plot_comparison(correlation, "y", use_bar_plot=False, save=False, show=False)
# Workaround for HTML rendering, instead of ``show=True``
plt.show()
Total running time of the script: ( 0 minutes 0.527 seconds)
