opt_problem module¶
Optimization problem.
The OptimizationProblem class operates on a DesignSpace defining:
an initial guess \(x_0\) for the design variables,
the bounds \(l_b \leq x \leq u_b\) of the design variables.
A (possible vector) objective function with an MDOFunction type
is set using the objective attribute.
If the optimization problem looks for the maximum of this objective function,
the OptimizationProblem.change_objective_sign()
changes the objective function sign
because the optimization drivers seek to minimize this objective function.
Equality and inequality constraints are also MDOFunction instances
provided to the OptimizationProblem
by means of its OptimizationProblem.add_constraint() method.
The OptimizationProblem allows to evaluate the different functions
for a given design parameters vector
(see OptimizationProblem.evaluate_functions()).
Note that this evaluation step relies on an automated scaling of function wrt the bounds
so that optimizers and DOE algorithms work
with inputs scaled between 0 and 1 for all the variables.
The OptimizationProblem has also a Database
that stores the calls to all the functions
so that no function is called twice with the same inputs.
Concerning the derivatives’ computation,
the OptimizationProblem automates
the generation of the finite differences or complex step wrappers on functions,
when the analytical gradient is not available.
Lastly,
various getters and setters are available,
as well as methods to export the Database
to an HDF file or to a Dataset for future post-processing.
- gemseo.algos.opt_problem.EvaluationType
The type of the output value of an evaluation.
- class gemseo.algos.opt_problem.OptimizationProblem(design_space, pb_type=ProblemType.LINEAR, input_database=None, differentiation_method=DifferentiationMethod.USER_GRAD, fd_step=1e-07, parallel_differentiation=False, use_standardized_objective=True, hdf_node_path='', **parallel_differentiation_options)[source]
Bases:
BaseProblemAn optimization problem.
Create an optimization problem from:
a
DesignSpacespecifying the design variables in terms of names, lower bounds, upper bounds and initial guesses,the objective function as an
MDOFunction, which can be a vector,
execute it from an algorithm provided by a
DriverLibrary, and store some execution data in aDatabase.In particular, this
Databasestores the calls to all the functions so that no function is called twice with the same inputs.An
OptimizationProblemalso has an automated scaling of function with respect to the bounds of the design variables so that the driving algorithms work with inputs scaled between 0 and 1.Lastly,
OptimizationProblemautomates the generation of finite differences or complex step wrappers on functions, when analytical gradient is not available.- Parameters:
design_space (DesignSpace) – The design space on which the functions are evaluated.
pb_type (ProblemType) –
The type of the optimization problem.
By default it is set to “linear”.
input_database (str | Path | Database | None) – A database to initialize that of the optimization problem. If
None, the optimization problem starts from an empty database.differentiation_method (DifferentiationMethod) –
The default differentiation method to be applied to the functions of the optimization problem.
By default it is set to “user”.
fd_step (float) –
The step to be used by the step-based differentiation methods.
By default it is set to 1e-07.
parallel_differentiation (bool) –
Whether to approximate the derivatives in
By default it is set to False.
parallel. –
use_standardized_objective (bool) –
Whether to use standardized objective for logging and post-processing.
By default it is set to True.
hdf_node_path (str) –
The path of the HDF node from which the database should be imported. If empty, the root node is considered.
By default it is set to “”.
**parallel_differentiation_options (int | bool) – The options to approximate the derivatives in parallel.
- AggregationFunction
alias of
EvaluationFunction
- class ApproximationMode(value)
Bases:
StrEnumThe approximation derivation modes.
- CENTERED_DIFFERENCES = 'centered_differences'
The centered differences method used to approximate the Jacobians by perturbing each variable with a small real number.
- COMPLEX_STEP = 'complex_step'
The complex step method used to approximate the Jacobians by perturbing each variable with a small complex number.
- FINITE_DIFFERENCES = 'finite_differences'
The finite differences method used to approximate the Jacobians by perturbing each variable with a small real number.
- class DifferentiationMethod(value)
Bases:
StrEnumThe differentiation methods.
- CENTERED_DIFFERENCES = 'centered_differences'
- COMPLEX_STEP = 'complex_step'
- FINITE_DIFFERENCES = 'finite_differences'
- NO_DERIVATIVE = 'no_derivative'
- USER_GRAD = 'user'
- class ProblemType(value)[source]
Bases:
StrEnumThe type of problem.
- LINEAR = 'linear'
- NON_LINEAR = 'non-linear'
- add_callback(callback_func, each_new_iter=True, each_store=False)[source]
Add a callback for some events.
The callback functions are attached to the database, which means they are triggered when new values are stored within the database of the optimization problem.
- Parameters:
callback_func (Callable[[ndarray], Any]) – A function to be called after some events, whose argument is a design vector.
each_new_iter (bool) –
Whether to evaluate the callback functions after evaluating all functions of the optimization problem for a given point and storing their values in the
database.By default it is set to True.
each_store (bool) –
Whether to evaluate the callback functions after storing any new value in the
database.By default it is set to False.
- Return type:
None
- add_constraint(cstr_func, value=None, cstr_type=None, positive=False)[source]
Add a constraint (equality and inequality) to the optimization problem.
- Parameters:
cstr_func (MDOFunction) – The constraint.
value (float | None) – The value for which the constraint is active. If
None, this value is 0.cstr_type (MDOFunction.ConstraintType | None) – The type of the constraint.
positive (bool) –
If
True, then the inequality constraint is positive.By default it is set to False.
- Raises:
TypeError – When the constraint of a linear optimization problem is not an
MDOLinearFunction.ValueError – When the type of the constraint is missing.
- Return type:
None
- add_eq_constraint(cstr_func, value=None)[source]
Add an equality constraint to the optimization problem.
- Parameters:
cstr_func (MDOFunction) – The constraint.
value (float | None) – The value for which the constraint is active. If
None, this value is 0.
- Return type:
None
- add_ineq_constraint(cstr_func, value=None, positive=False)[source]
Add an inequality constraint to the optimization problem.
- Parameters:
cstr_func (MDOFunction) – The constraint.
value (float | None) – The value for which the constraint is active. If
None, this value is 0.positive (bool) –
If
True, then the inequality constraint is positive.By default it is set to False.
- Return type:
None
- add_observable(obs_func, new_iter=True)[source]
Add a function to be observed.
When the
OptimizationProblemis executed, the observables are called following this sequence:The optimization algorithm calls the objective function with a normalized
x_vect.The
OptimizationProblem.preprocess_functions()wraps the function as aNormDBFunction, which unnormalizes thex_vectbefore evaluation.The unnormalized
x_vectand the result of the evaluation are stored in theOptimizationProblem.database.The previous step triggers the
OptimizationProblem.new_iter_listeners, which calls the observables with the unnormalizedx_vect.The observables themselves are wrapped as a
NormDBFunctionbyOptimizationProblem.preprocess_functions(), but in this case the input is always expected as unnormalized to avoid an additional normalizing-unnormalizing step.Finally, the output is stored in the
OptimizationProblem.database.
- Parameters:
obs_func (MDOFunction) – An observable to be observed.
new_iter (bool) –
If
True, then the observable will be called at each new iterate.By default it is set to True.
- Return type:
None
- aggregate_constraint(constraint_index, method=EvaluationFunction.MAX, groups=None, **options)[source]
Aggregate a constraint to generate a reduced dimension constraint.
- Parameters:
constraint_index (int) – The index of the constraint in
constraints.method (Callable[[NDArray[float]], float] | AggregationFunction) –
The aggregation method, e.g.
"max","lower_bound_KS","upper_bound_KS"``or ``"IKS".By default it is set to “MAX”.
groups (Iterable[Sequence[int]] | None) – The groups of components of the constraint to aggregate to produce one aggregation constraint per group of components; if
None, a single aggregation constraint is produced.**options (Any) – The options of the aggregation method.
- Raises:
ValueError – When the given index is greater or equal than the number of constraints or when the constraint aggregation method is unknown.
- Return type:
None
- apply_exterior_penalty(objective_scale=1.0, scale_inequality=1.0, scale_equality=1.0)[source]
Reformulate the optimization problem using exterior penalty.
Given the optimization problem with equality and inequality constraints:
\[ \begin{align}\begin{aligned}min_x f(x)\\s.t.\\g(x)\leq 0\\h(x)=0\\l_b\leq x\leq u_b\end{aligned}\end{align} \]The exterior penalty approach consists in building a penalized objective function that takes into account constraints violations:
\[ \begin{align}\begin{aligned}min_x \tilde{f}(x) = \frac{f(x)}{o_s} + s[\sum{H(g(x))g(x)^2}+\sum{h(x)^2}]\\s.t.\\l_b\leq x\leq u_b\end{aligned}\end{align} \]Where \(H(x)\) is the Heaviside function, \(o_s\) is the
objective_scaleparameter and \(s\) is the scale parameter. The solution of the new problem approximate the one of the original problem. Increasing the values ofobjective_scaleand scale, the solutions are closer but the optimization problem requires more and more iterations to be solved.- Parameters:
scale_equality (float | ndarray) –
The equality constraint scaling constant.
By default it is set to 1.0.
objective_scale (float) –
The objective scaling constant.
By default it is set to 1.0.
scale_inequality (float | ndarray) –
The inequality constraint scaling constant.
By default it is set to 1.0.
- Return type:
None
- change_objective_sign()[source]
Change the objective function sign in order to minimize its opposite.
The
OptimizationProblemexpresses any optimization problem as a minimization problem. Then, an objective function originally expressed as a performance function to maximize must be converted into a cost function to minimize, by means of this method.- Return type:
None
- check()[source]
Check if the optimization problem is ready for run.
- Raises:
ValueError – If the objective function is missing.
- Return type:
None
- static check_format(input_function)[source]
Check that a function is an instance of
MDOFunction.- Parameters:
input_function (Any) – The function to be tested.
- Raises:
TypeError – If the function is not an
MDOFunction.- Return type:
None
- clear_listeners()[source]
Clear all the listeners.
- Return type:
None
- evaluate_functions(x_vect=None, eval_jac=False, eval_obj=True, eval_observables=True, normalize=True, no_db_no_norm=False, constraint_names=None, observable_names=None, jacobian_names=None)[source]
Compute the functions of interest, and possibly their derivatives.
These functions of interest are the constraints, and possibly the objective.
Some optimization libraries require the number of constraints as an input parameter which is unknown by the formulation or the scenario. Evaluation of initial point allows to get this mandatory information. This is also used for design of experiments to evaluate samples.
- Parameters:
x_vect (ndarray) – The input vector at which the functions must be evaluated; if None, the initial point x_0 is used.
eval_jac (bool) –
Whether to compute the Jacobian matrices of the functions of interest. If
Trueandjacobian_namesisNonethen compute the Jacobian matrices (or gradients) of the functions that are selected for evaluation (witheval_obj,constraint_names,eval_observablesand``observable_names``). IfFalseandjacobian_namesisNonethen no Jacobian matrix is evaluated. Ifjacobian_namesis notNonethen the value ofeval_jacis ignored.By default it is set to False.
eval_obj (bool) –
Whether to consider the objective function as a function of interest.
By default it is set to True.
eval_observables (bool) –
Whether to evaluate the observables. If
Trueandobservable_namesisNonethen all the observables are evaluated. IfFalseandobservable_namesisNonethen no observable is evaluated. Ifobservable_namesis notNonethen the value ofeval_observablesis ignored.By default it is set to True.
normalize (bool) –
Whether to consider the input vector
x_vectnormalized.By default it is set to True.
no_db_no_norm (bool) –
If
True, then do not use the pre-processed functions, so we have no database, nor normalization.By default it is set to False.
constraint_names (Iterable[str] | None) – The names of the constraints to evaluate. If
Nonethen all the constraints are evaluated.observable_names (Iterable[str] | None) – The names of the observables to evaluate. If
Noneandeval_observablesisTruethen all the observables are evaluated. IfNoneandeval_observablesisFalsethen no observable is evaluated.jacobian_names (Iterable[str] | None) – The names of the functions whose Jacobian matrices (or gradients) to compute. If
Noneandeval_jacisTruethen compute the Jacobian matrices (or gradients) of the functions that are selected for evaluation (witheval_obj,constraint_names,eval_observablesand``observable_names``). IfNoneandeval_jacisFalsethen no Jacobian matrix is computed.
- Returns:
The output values of the functions of interest, as well as their Jacobian matrices if
eval_jacisTrue.- Raises:
ValueError – If a name in
jacobian_namesis not the name of a function of the problem.- Return type:
EvaluationType
- execute_observables_callback(last_x)[source]
The callback function to be passed to the database.
Call all the observables with the last design variables values as argument.
- Parameters:
last_x (ndarray) – The design variables values from the last evaluation.
- Return type:
None
- classmethod from_hdf(file_path, x_tolerance=0.0, hdf_node_path='')[source]
Import an optimization history from an HDF file.
- Parameters:
file_path (str | Path) – The file containing the optimization history.
x_tolerance (float) –
The tolerance on the design variables when reading the file.
By default it is set to 0.0.
hdf_node_path (str) –
The path of the HDF node from which the database should be imported. If empty, the root node is considered.
By default it is set to “”.
- Returns:
The read optimization problem.
- Return type:
- get_active_ineq_constraints(x_vect, tol=1e-06)[source]
For each constraint, indicate if its different components are active.
- Parameters:
- Returns:
For each constraint, a boolean indicator of activation of its different components.
- Return type:
- get_all_function_name()[source]
Retrieve the names of all the function of the optimization problem.
These functions are the constraints, the objective function and the observables.
- get_all_functions(original=False)[source]
Retrieve all the functions of the optimization problem.
These functions are the constraints, the objective function and the observables.
- Parameters:
original (bool) –
Whether to return the original functions or the preprocessed ones.
By default it is set to False.
- Returns:
All the functions of the optimization problem.
- Return type:
- get_best_infeasible_point()[source]
Retrieve the best infeasible point within a given tolerance.
- get_constraint_names()[source]
Retrieve the names of the constraints.
- get_constraints_number()[source]
Retrieve the number of constraints.
- Returns:
The number of constraints.
- Return type:
- get_data_by_names(names, as_dict=True, filter_non_feasible=False)[source]
Return the data for specific names of variables.
- Parameters:
- Returns:
The data related to the variables.
- Return type:
- get_design_variable_names()[source]
Retrieve the names of the design variables.
- get_dimension()[source]
Retrieve the total number of design variables.
- Returns:
The dimension of the design space.
- Return type:
- get_eq_constraints()[source]
Retrieve all the equality constraints.
- Returns:
The equality constraints.
- Return type:
- get_eq_constraints_number()[source]
Retrieve the number of equality constraints.
- Returns:
The number of equality constraints.
- Return type:
- get_eq_cstr_total_dim()[source]
Retrieve the total dimension of the equality constraints.
This dimension is the sum of all the outputs dimensions of all the equality constraints.
- Returns:
The total dimension of the equality constraints.
- Return type:
- get_feasible_points()[source]
Retrieve the feasible points within a given tolerance.
This tolerance is defined by
OptimizationProblem.eq_tolerancefor equality constraints andOptimizationProblem.ineq_tolerancefor inequality ones.
- get_function_dimension(name)[source]
Return the dimension of a function of the problem (e.g. a constraint).
- Parameters:
name (str) – The name of the function.
- Returns:
The dimension of the function.
- Raises:
ValueError – If the function name is unknown to the problem.
RuntimeError – If the function dimension is not unavailable.
- Return type:
- get_function_names(names)[source]
Return the names of the functions stored in the database.
- get_functions_dimensions(names=None)[source]
Return the dimensions of the outputs of the problem functions.
- Parameters:
names (Iterable[str] | None) – The names of the functions. If
None, then the objective and all the constraints are considered.- Returns:
The dimensions of the outputs of the problem functions. The dictionary keys are the functions names and the values are the functions dimensions.
- Return type:
- get_ineq_constraints()[source]
Retrieve all the inequality constraints.
- Returns:
The inequality constraints.
- Return type:
- get_ineq_constraints_number()[source]
Retrieve the number of inequality constraints.
- Returns:
The number of inequality constraints.
- Return type:
- get_ineq_cstr_total_dim()[source]
Retrieve the total dimension of the inequality constraints.
This dimension is the sum of all the outputs dimensions of all the inequality constraints.
- Returns:
The total dimension of the inequality constraints.
- Return type:
- get_last_point()[source]
Return the last design point.
- Returns:
The last point result, defined by:
the value of the objective function,
the value of the design variables,
the indicator of feasibility of the last point,
the value of the constraints,
the value of the gradients of the constraints.
- Raises:
ValueError – When the optimization database is empty.
- Return type:
tuple[ndarray, ndarray, bool, dict[str, ndarray], dict[str, ndarray]]
- get_nonproc_constraints()[source]
Retrieve the non-processed constraints.
- Returns:
The non-processed constraints.
- Return type:
- get_nonproc_objective()[source]
Retrieve the non-processed objective function.
- Return type:
- get_number_of_unsatisfied_constraints(design_variables, values=mappingproxy({}))[source]
Return the number of scalar constraints not satisfied by design variables.
- Parameters:
- Returns:
The number of unsatisfied scalar constraints.
- Return type:
- get_objective_name(standardize=True)[source]
Retrieve the name of the objective function.
- get_observable(name)[source]
Return an observable of the problem.
- Parameters:
name (str) – The name of the observable.
- Returns:
The pre-processed observable if the functions of the problem have already been pre-processed, otherwise the original one.
- Return type:
- get_optimum()[source]
Return the optimum solution within a given feasibility tolerances.
- Returns:
The optimum result, defined by:
the value of the objective function,
the value of the design variables,
the indicator of feasibility of the optimal solution,
the value of the constraints,
the value of the gradients of the constraints.
- Raises:
ValueError – When the optimization database is empty.
- Return type:
tuple[ndarray, ndarray, bool, dict[str, ndarray], dict[str, ndarray]]
- get_reformulated_problem_with_slack_variables()[source]
Add slack variables and replace inequality constraints with equality ones.
Given the original optimization problem,
\[ \begin{align}\begin{aligned}min_x f(x)\\s.t.\\g(x)\leq 0\\h(x)=0\\l_b\leq x\leq u_b\end{aligned}\end{align} \]Slack variables are introduced for all inequality constraints that are non-positive. An equality constraint for each slack variable is then defined.
\[ \begin{align}\begin{aligned}min_{x,s} F(x,s) = f(x)\\s.t.\\H(x,s) = h(x)=0\\G(x,s) = g(x)-s=0\\l_b\leq x\leq u_b\\s\leq 0\end{aligned}\end{align} \]- Returns:
An optimization problem without inequality constraints.
- Return type:
- get_scalar_constraint_names()[source]
Return the names of the scalar constraints.
- get_violation_criteria(x_vect)[source]
Check if a design point is feasible and measure its constraint violation.
The constraint violation measure at a design point \(x\) is
\[\lVert\max(g(x)-\varepsilon_{\text{ineq}},0)\rVert_2^2 +\lVert|\max(|h(x)|-\varepsilon_{\text{eq}},0)\rVert_2^2\]where \(\|.\|_2\) is the Euclidean norm, \(g(x)\) is the inequality constraint vector, \(h(x)\) is the equality constraint vector, \(\varepsilon_{\text{ineq}}\) is the tolerance for the inequality constraints and \(\varepsilon_{\text{eq}}\) is the tolerance for the equality constraints.
If the design point is feasible, the constraint violation measure is 0.
- get_x0_normalized(cast_to_real=False, as_dict=False)[source]
Return the initial values of the design variables after normalization.
- Parameters:
- Returns:
The current values of the design variables normalized between 0 and 1 from their lower and upper bounds.
- Return type:
- has_constraints()[source]
Check if the problem has equality or inequality constraints.
- Returns:
True if the problem has equality or inequality constraints.
- Return type:
- has_eq_constraints()[source]
Check if the problem has equality constraints.
- Returns:
True if the problem has equality constraints.
- Return type:
- has_ineq_constraints()[source]
Check if the problem has inequality constraints.
- Returns:
True if the problem has inequality constraints.
- Return type:
- has_nonlinear_constraints()[source]
Check if the problem has non-linear constraints.
- Returns:
True if the problem has equality or inequality constraints.
- Return type:
- is_max_iter_reached()[source]
Check if the maximum amount of iterations has been reached.
- Returns:
Whether the maximum amount of iterations has been reached.
- Return type:
- is_point_feasible(out_val, constraints=None)[source]
Check if a point is feasible.
Notes
If the value of a constraint is absent from this point, then this constraint will be considered satisfied.
- Parameters:
out_val (dict[str, ndarray]) – The values of the objective function, and eventually constraints.
constraints (Iterable[MDOFunction] | None) – The constraints whose values are to be tested. If
None, then take all constraints of the problem.
- Returns:
The feasibility of the point.
- Return type:
- preprocess_functions(is_function_input_normalized=True, use_database=True, round_ints=True, eval_obs_jac=False, support_sparse_jacobian=False)[source]
Pre-process all the functions and eventually the gradient.
Required to wrap the objective function and constraints with the database and eventually the gradients by complex step or finite differences.
- Parameters:
is_function_input_normalized (bool) –
Whether to consider the function input as normalized and unnormalize it before the evaluation takes place.
By default it is set to True.
use_database (bool) –
Whether to wrap the functions in the database.
By default it is set to True.
round_ints (bool) –
Whether to round the integer variables.
By default it is set to True.
eval_obs_jac (bool) –
Whether to evaluate the Jacobian of the observables.
By default it is set to False.
support_sparse_jacobian (bool) –
Whether the driver support sparse Jacobian.
By default it is set to False.
- Return type:
None
- static repr_constraint(func, cstr_type, value=None, positive=False)[source]
Express a constraint as a string expression.
- Parameters:
func (MDOFunction) – The constraint function.
cstr_type (MDOFunction.ConstraintType) – The type of the constraint.
value (float | None) – The value for which the constraint is active. If
None, this value is 0.positive (bool) –
If
True, then the inequality constraint is positive.By default it is set to False.
- Returns:
A string representation of the constraint.
- Return type:
- reset(database=True, current_iter=True, design_space=True, function_calls=True, preprocessing=True)[source]
Partially or fully reset the optimization problem.
- Parameters:
database (bool) –
Whether to clear the database.
By default it is set to True.
current_iter (bool) –
Whether to reset the current iteration
OptimizationProblem.current_iter.By default it is set to True.
design_space (bool) –
Whether to reset the current point of the
OptimizationProblem.design_spaceto its initial value (possibly none).By default it is set to True.
function_calls (bool) –
Whether to reset the number of calls of the functions.
By default it is set to True.
preprocessing (bool) –
Whether to turn the pre-processing of functions to False.
By default it is set to True.
- Return type:
None
- to_dataset(name='', categorize=True, opt_naming=True, export_gradients=False, input_values=())[source]
Export the database of the optimization problem to a
Dataset.The variables can be classified into groups:
Dataset.DESIGN_GROUPorDataset.INPUT_GROUPfor the design variables andDataset.FUNCTION_GROUPorDataset.OUTPUT_GROUPfor the functions (objective, constraints and observables).- Parameters:
name (str) –
The name to be given to the dataset. If empty, use the name of the
OptimizationProblem.database.By default it is set to “”.
categorize (bool) –
Whether to distinguish between the different groups of variables. Otherwise, group all the variables in
Dataset.PARAMETER_GROUP`.By default it is set to True.
opt_naming (bool) –
Whether to use
Dataset.DESIGN_GROUPandDataset.FUNCTION_GROUPas groups. Otherwise, useDataset.INPUT_GROUPandDataset.OUTPUT_GROUP.By default it is set to True.
export_gradients (bool) –
Whether to export the gradients of the functions (objective function, constraints and observables) if the latter are available in the database of the optimization problem.
By default it is set to False.
input_values (Iterable[ndarray]) –
The input values to be considered. If empty, consider all the input values of the database.
By default it is set to ().
- Returns:
A dataset built from the database of the optimization problem.
- Return type:
- to_hdf(file_path, append=False, hdf_node_path='')[source]
Export the optimization problem to an HDF file.
- Parameters:
file_path (str | Path) – The path of the file to store the data.
append (bool) –
If
True, then the data are appended to the file if not empty.By default it is set to False.
hdf_node_path (str) –
The path of the HDF node in which the database should be exported. If empty, the root node is considered.
By default it is set to “”.
- Return type:
None
- CONSTRAINTS_GROUP: Final[str] = 'constraints'
- DESIGN_SPACE_ATTRS: Final[str] = ['u_bounds', 'l_bounds', 'x_0', 'x_names', 'dimension']
- DESIGN_SPACE_GROUP: Final[str] = 'design_space'
- DESIGN_VAR_NAMES: Final[str] = 'x_names'
- DESIGN_VAR_SIZE: Final[str] = 'x_size'
- FUNCTIONS_ATTRS: ClassVar[str] = ['objective', 'constraints']
- GGOBI_FORMAT: Final[str] = 'ggobi'
- HDF5_FORMAT: Final[str] = 'hdf5'
- HDF_NODE_PATH: Final[str] = 'hdf_node_path'
- KKT_RESIDUAL_NORM: Final[str] = 'KKT residual norm'
- OBJECTIVE_GROUP: Final[str] = 'objective'
- OBSERVABLES_GROUP: Final[str] = 'observables'
- OPTIM_DESCRIPTION: ClassVar[str] = ['minimize_objective', 'fd_step', 'differentiation_method', 'pb_type', 'ineq_tolerance', 'eq_tolerance']
- OPT_DESCR_GROUP: Final[str] = 'opt_description'
- SOLUTION_GROUP: Final[str] = 'solution'
- activate_bound_check: ClassVar[bool] = True
Whether to check if a point is in the design space before calling functions.
- property constraint_names: dict[str, list[str]]
The standardized constraint names bound to the original ones.
- constraints: list[MDOFunction]
The constraints.
- current_iter: int
The current iteration.
- database: Database
The database to store the optimization problem data.
- design_space: DesignSpace
The design space on which the optimization problem is solved.
- property dimension: int
The dimension of the design space.
- eq_tolerance: float
The tolerance for the equality constraints.
- fd_step: float
The finite differences step.
- ineq_tolerance: float
The tolerance for the inequality constraints.
- property is_mono_objective: bool
Whether the optimization problem is mono-objective.
- Raises:
ValueError – When the dimension of the objective cannot be determined.
- max_iter: int
The maximum iteration.
- property minimize_objective: bool
Whether to minimize the objective.
- new_iter_observables: list[MDOFunction]
The observables to be called at each new iterate.
- nonproc_constraints: list[MDOFunction]
The non-processed constraints.
- nonproc_new_iter_observables: list[MDOFunction]
The non-processed observables to be called at each new iterate.
- nonproc_objective: MDOFunction
The non-processed objective function.
- nonproc_observables: list[MDOFunction]
The non-processed observables.
- property objective: MDOFunction
The objective function.
- observables: list[MDOFunction]
The observables.
- property parallel_differentiation: bool
Whether to approximate the derivatives in parallel.
- property parallel_differentiation_options: dict[str, int | bool]
The options to approximate the derivatives in parallel.
- pb_type: ProblemType
The type of optimization problem.
- preprocess_options: dict
The options to pre-process the functions.
- solution: OptimizationResult | None
The solution of the optimization problem if solved; otherwise
None.
- stop_if_nan: bool
Whether the optimization stops when a function returns
NaN.
- use_standardized_objective: bool
Whether to use standardized objective for logging and post-processing.
The standardized objective corresponds to the original one expressed as a cost function to minimize. A
DriverLibraryworks with this standardized objective and theDatabasestores its values. However, for convenience, it may be more relevant to log the expression and the values of the original objective.
Examples using OptimizationProblem¶
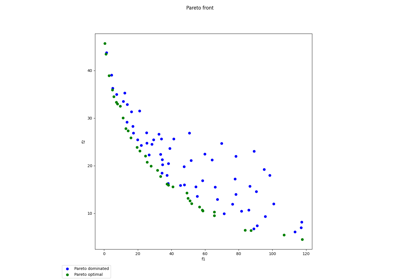
Multi-objective Binh-Korn example with the mNBI algorithm
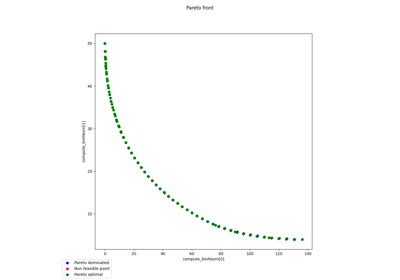
Multi-objective Fonseca-Fleming example with the mNBI algorithm
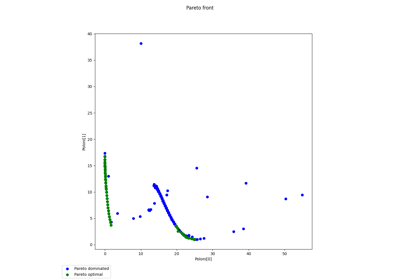
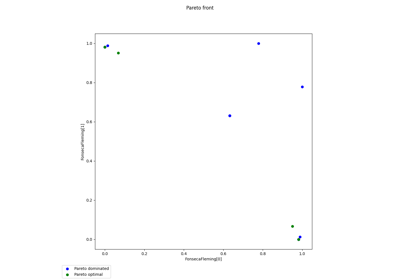
Multi-objective Poloni example with the mNBI algorithm