gemseo / uncertainty / sensitivity / morris

analysis module¶

Class for the estimation of Morris indices.

OAT technique¶

The purpose of the One-At-a-Time (OAT) methodology is to quantify the elementary effect

\[df_i = f(X_1+dX_1,\ldots,X_{i-1}+dX_{i-1},X_i+dX_i,\ldots,X_d) - f(X_1+dX_1,\ldots,X_{i-1}+dX_{i-1},X_i,\ldots,X_d)\]

associated with a small variation \(dX_i\) of \(X_i\) with

\[df_1 = f(X_1+dX_1,\ldots,X_d)-f(X_1,\ldots,X_d)\]

The elementary effects \(df_1,\ldots,df_d\) are computed sequentially from an initial point

\[X=(X_1,\ldots,X_d)\]

From these elementary effects, we can compare their absolute values \(|df_1|,\ldots,|df_d|\) and sort \(X_1,\ldots,X_d\) accordingly.

Morris technique¶

Then, the purpose of the Morris’ methodology is to repeat the OAT method from different initial points \(X^{(1)},\ldots,X^{(r)}\) and compare the parameters in terms of mean

\[\mu_i^* = \frac{1}{r}\sum_{j=1}^r|df_i^{(j)}|\]

and standard deviation

\[\sigma_i = \sqrt{\frac{1}{r}\sum_{j=1}^r\left(|df_i^{(j)}|-\mu_i\right)^2}\]

where \(\mu_i = \frac{1}{r}\sum_{j=1}^rdf_i^{(j)}\).

This methodology relies on the MorrisAnalysis class.

class gemseo.uncertainty.sensitivity.morris.analysis.MorrisAnalysis(disciplines, parameter_space, n_samples, output_names=(), algo='', algo_options=mappingproxy({}), n_replicates=5, step=0.05, formulation='MDF', **formulation_options)[source]¶

Bases: SensitivityAnalysis

Sensitivity analysis based on the Morris’ indices.

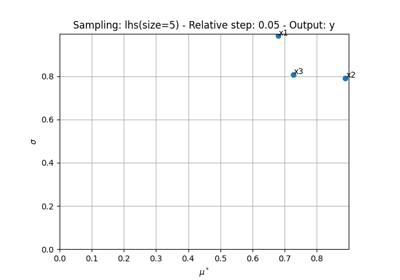
MorrisAnalysis.indices contains both \(\mu^*\), \(\mu\) and \(\sigma\) while MorrisAnalysis.main_indices represents \(\mu^*\). Lastly, the MorrisAnalysis.plot() method represents the parameters as a scatter plot where \(X_i\) has as coordinates \((\mu_i^*,\sigma_i)\). The bigger \(\mu_i^*\) is, the more significant \(X_i\) is. Concerning \(\sigma_i\), it highlights non-linear effects along \(X_i\) or cross-effects between \(X_i\) and other parameter(s).

The user can specify the DOE algorithm name to select the initial points, as well as the number of replicates and the relative step for the input variations.

Examples

>>> from numpy import pi
>>> from gemseo import create_discipline, create_parameter_space
>>> from gemseo.uncertainty.sensitivity.morris.analysis import MorrisAnalysis
>>>
>>> expressions = {"y": "sin(x1)+7*sin(x2)**2+0.1*x3**4*sin(x1)"}
>>> discipline = create_discipline(
...     "AnalyticDiscipline", expressions=expressions
... )
>>>
>>> parameter_space = create_parameter_space()
>>> parameter_space.add_random_variable(
...     "x1", "OTUniformDistribution", minimum=-pi, maximum=pi
... )
>>> parameter_space.add_random_variable(
...     "x2", "OTUniformDistribution", minimum=-pi, maximum=pi
... )
>>> parameter_space.add_random_variable(
...     "x3", "OTUniformDistribution", minimum=-pi, maximum=pi
... )
>>>
>>> analysis = MorrisAnalysis([discipline], parameter_space, n_samples=None)
>>> indices = analysis.compute_indices()

Parameters:

disciplines (Collection[MDODiscipline]) – The discipline or disciplines to use for the analysis.
parameter_space (ParameterSpace) – A parameter space.
n_samples (int | None) – A number of samples. If None, the number of samples is computed by the algorithm.
output_names (Iterable[str]) –
The disciplines’ outputs to be considered for the analysis. If empty, use all the outputs.

By default it is set to ().
algo (str) –
The name of the DOE algorithm. If empty, use the SensitivityAnalysis.DEFAULT_DRIVER.

By default it is set to “”.
algo_options (Mapping[str, DOELibraryOptionType]) –
The options of the DOE algorithm.

By default it is set to {}.
n_replicates (int) –
The number of times the OAT method is repeated. Used only if n_samples is None. Otherwise, this number is the greater integer \(r\) such that \(r(d+1)\leq\) n_samples and \(r(d+1)\) is the number of samples actually carried out.

By default it is set to 5.
step (float) –
The finite difference step of the OAT method.

By default it is set to 0.05.
formulation (str) –
The name of the MDOFormulation to sample the disciplines.

By default it is set to “MDF”.
**formulation_options (Any) – The options of the MDOFormulation.

Raises:

ValueError – If at least one input dimension is not equal to 1.

class Method(value)[source]¶

Bases: StrEnum

The names of the sensitivity methods.

MU_STAR = 'MU_STAR'¶: The mean of the absolute finite difference.

SIGMA = 'SIGMA'¶: The standard deviation of the absolute finite difference.

compute_indices(outputs=(), normalize=False)[source]¶

Compute the sensitivity indices.

Parameters:

outputs (str | Sequence[str]) –
The name(s) of the output(s) for which to compute the sensitivity indices. If empty, use the names of the outputs set at instantiation.

By default it is set to ().
normalize (bool) –
Whether to normalize the indices with the empirical bounds of the outputs.

By default it is set to False.

Returns:

The sensitivity indices.

With the following structure:

{
    "method_name": {
        "output_name": [
            {
                "input_name": data_array,
            }
        ]
    }
}

Return type:

dict[str, FirstOrderIndicesType]

static from_pickle(file_path)¶

Load a sensitivity analysis from the disk.

Parameters:: file_path (str | Path) – The path to the file.
Returns:: The sensitivity analysis.
Return type:: SensitivityAnalysis

plot(output, inputs=(), title='', save=True, show=False, file_path='', directory_path='', file_name='', file_format='', offset=1, lower_mu=None, lower_sigma=None)[source]¶

Plot the Morris indices for each input variable.

For \(i\in\{1,\ldots,d\}\), plot \(\mu_i^*\) in function of \(\sigma_i\).

Parameters:

output (VariableType) – The output for which to display sensitivity indices, either a name or a tuple of the form (name, component). If name, its first component is considered.
inputs (Iterable[str]) –
The uncertain input variables for which to display the sensitivity indices. If empty, display all the uncertain input variables.

By default it is set to ().
title (str) –
The title of the plot, if any.

By default it is set to “”.
save (bool) –
If True, save the figure.

By default it is set to True.
show (bool) –
If True, show the figure.

By default it is set to False.
file_path (str | Path) –
A file path. Either a complete file path, a directory name or a file name. If empty, use a default file name and a default directory. The file extension is inferred from filepath extension, if any.

By default it is set to “”.
directory_path (str | Path) –
The path to the directory where to save the plots.

By default it is set to “”.
file_name (str) –
The name of the file.

By default it is set to “”.
file_format (str) –
A file format, e.g. ‘png’, ‘pdf’, ‘svg’, … Used when file_path does not have any extension. If empty, use a default file extension.

By default it is set to “”.
offset (float) –
The offset to display the inputs names, expressed as a percentage applied to both x-range and y-range.

By default it is set to 1.
lower_mu (float | None) – The lower bound for \(\mu\). If None, use a default value.
lower_sigma (float | None) – The lower bound for \(\sigma\). If None, use a default value.

Returns:

The plot figure.

Return type:

Figure

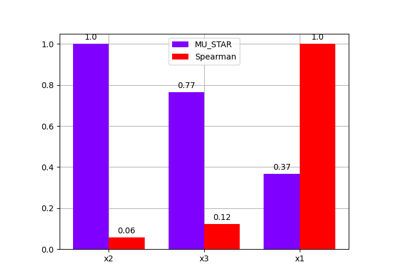
plot_bar(outputs=(), inputs=(), standardize=False, title='', save=True, show=False, file_path='', directory_path='', file_name='', file_format='', sort=True, sorting_output='', **options)¶

Plot the sensitivity indices on a bar chart.

This method may consider one or more outputs, as well as all inputs (default behavior) or a subset.

Parameters:

outputs (OutputsType) –
The outputs for which to display sensitivity indices, either a name, a list of names, a (name, component) tuple, a list of such tuples or a list mixing such tuples and names. When a name is specified, all its components are considered. If empty, use the default outputs.

By default it is set to ().
inputs (Iterable[str]) –
The uncertain input variables for which to display the sensitivity indices. If empty, display all the uncertain input variables.

By default it is set to ().
standardize (bool) –
Whether to scale the indices to \([0,1]\).

By default it is set to False.
title (str) –
The title of the plot, if any.

By default it is set to “”.
save (bool) –
If True, save the figure.

By default it is set to True.
show (bool) –
If True, show the figure.

By default it is set to False.
file_path (str | Path) –
The path of the file to save the figures. If the extension is missing, use file_extension. If empty, create a file path from directory_path, file_name and file_extension.

By default it is set to “”.
directory_path (str | Path) –
The path of the directory to save the figures. If empty, use the current working directory.

By default it is set to “”.
file_name (str) –
The name of the file to save the figures. If empty, use a default one generated by the post-processing.

By default it is set to “”.
file_format (str) –
A file extension, e.g. ‘png’, ‘pdf’, ‘svg’, … If None, use a default file extension.

By default it is set to “”.
**options (int) – The options to instantiate the BarPlot. If empty, use a default file extension.
sort (bool) –
Whether to sort the uncertain variables by decreasing order of the sensitivity indices associated with the sorting output variable.

By default it is set to True.
sorting_output (VariableType) –
The sorting output variable If empty, use the first one.

By default it is set to “”.
**options – The options to instantiate the BarPlot.

Returns:

A bar chart representing the sensitivity indices.

Return type:

BarPlot

plot_comparison(indices, output, inputs=(), title='', use_bar_plot=True, save=True, show=False, file_path='', directory_path='', file_name='', file_format='', **options)¶

Plot a comparison between the current sensitivity indices and other ones.

This method allows to use either a bar chart (default option) or a radar one.

Parameters:

indices (list[SensitivityAnalysis]) – The sensitivity indices.
output (VariableType) – The output for which to display sensitivity indices, either a name or a tuple of the form (name, component). If name, its first component is considered.
inputs (Iterable[str]) –
The uncertain input variables for which to display the sensitivity indices. If empty, display all the uncertain input variables.

By default it is set to ().
title (str) –
The title of the plot, if any.

By default it is set to “”.
use_bar_plot (bool) –
The type of graph. If True, use a bar plot. Otherwise, use a radar chart.

By default it is set to True.
save (bool) –
If True, save the figure.

By default it is set to True.
show (bool) –
If True, show the figure.

By default it is set to False.
file_path (str | Path) –
The path of the file to save the figures. If empty, create a file path from directory_path, file_name and file_format.

By default it is set to “”.
directory_path (str | Path) –
The path of the directory to save the figures. If empty, use the current working directory.

By default it is set to “”.
file_name (str) –
The name of the file to save the figures. If empty, use a default one generated by the post-processing.

By default it is set to “”.
file_format (str) –
A file format, e.g. ‘png’, ‘pdf’, ‘svg’, … If empty, use a default file extension.

By default it is set to “”.
**options (bool) – The options passed to the underlying DatasetPlot.

Returns:

A graph comparing sensitivity indices.

Return type:

BarPlot | RadarChart

plot_field(output, mesh=None, inputs=(), standardize=False, title='', save=True, show=False, file_path='', directory_path='', file_name='', file_format='', properties=mappingproxy({}))¶

Plot the sensitivity indices related to a 1D or 2D functional output.

The output is considered as a 1D or 2D functional variable, according to the shape of the mesh on which it is represented.

Parameters:

output (VariableType) – The output for which to display sensitivity indices, either a name or a tuple of the form (name, component) where (name, component) is used to sort the inputs. If it is a name, its first component is considered.
mesh (ndarray | None) – The mesh on which the p-length output is represented. Either a p-length array for a 1D functional output or a (p, 2) array for a 2D one. If None, assume a 1D functional output.
inputs (Iterable[str]) –
The uncertain input variables for which to display the sensitivity indices. If empty, display all the uncertain input variables.

By default it is set to ().
standardize (bool) –
Whether to scale the indices to \([0,1]\).

By default it is set to False.
title (str) –
The title of the plot, if any.

By default it is set to “”.
save (bool) –
If True, save the figure.

By default it is set to True.
show (bool) –
If True, show the figure.

By default it is set to False.
file_path (str | Path) –
The path of the file to save the figures. If empty, create a file path from directory_path, file_name and file_extension.

By default it is set to “”.
directory_path (str | Path) –
The path of the directory to save the figures. If empty, use the current working directory.

By default it is set to “”.
file_name (str) –
The name of the file to save the figures. If empty, use a default one generated by the post-processing.

By default it is set to “”.
file_format (str) –
A file extension, e.g. ‘png’, ‘pdf’, ‘svg’, … If empty, use a default file extension.

By default it is set to “”.
properties (Mapping[str, DatasetPlotPropertyType]) –
The general properties of a DatasetPlot.

By default it is set to {}.

Returns:

A bar plot representing the sensitivity indices.

Raises:

NotImplementedError – If the dimension of the mesh is greater than 2.

Return type:

Curves | Surfaces

plot_radar(outputs=(), inputs=(), standardize=False, title='', save=True, show=False, file_path='', directory_path='', file_name='', file_format='', min_radius=None, max_radius=None, sort=True, sorting_output='', **options)¶

Plot the sensitivity indices on a radar chart.

This method may consider one or more outputs, as well as all inputs (default behavior) or a subset.

For visualization purposes, it is also possible to change the minimum and maximum radius values.

Parameters:

outputs (OutputsType) –
The outputs for which to display sensitivity indices, either a name, a list of names, a (name, component) tuple, a list of such tuples or a list mixing such tuples and names. When a name is specified, all its components are considered. If empty, use the default outputs.

By default it is set to ().
inputs (Iterable[str]) –
The uncertain input variables for which to display the sensitivity indices. If empty, display all the uncertain input variables.

By default it is set to ().
standardize (bool) –
Whether to scale the indices to \([0,1]\).

By default it is set to False.
title (str) –
The title of the plot, if any.

By default it is set to “”.
save (bool) –
If True, save the figure.

By default it is set to True.
show (bool) –
If True, show the figure.

By default it is set to False.
file_path (str | Path) –
The path of the file to save the figures. If the extension is missing, use file_extension. If empty, create a file path from directory_path, file_name and file_extension.

By default it is set to “”.
directory_path (str | Path) –
The path of the directory to save the figures. If empty, use the current working directory.

By default it is set to “”.
file_name (str) –
The name of the file to save the figures. If empty, use a default one generated by the post-processing.

By default it is set to “”.
file_format (str) –
A file extension, e.g. ‘png’, ‘pdf’, ‘svg’, … If empty, use a default file extension.

By default it is set to “”.
min_radius (float | None) – The minimal radial value. If None, from data.
max_radius (float | None) – The maximal radial value. If None, from data.
sort (bool) –
Whether to sort the uncertain variables by decreasing order of the sensitivity indices associated with the sorting output variable.

By default it is set to True.
sorting_output (VariableType) –
The sorting output variable If empty, use the first one.

By default it is set to “”.
**options (bool | int) – The options to instantiate the RadarChart.

Returns:

A radar chart representing the sensitivity indices.

Return type:

RadarChart

sort_parameters(output)¶

Return the parameters sorted in descending order.

Parameters:: output (VariableType) – Either a tuple as (output_name, output_component) or an output name; in the second case, use the first output component.
Returns:: The input parameters sorted by decreasing order of sensitivity; in case of a multivariate input, aggregate the sensitivity indices associated to the different input components by adding them up typically.
Return type:: list[str]

static standardize_indices(indices)¶

Standardize the sensitivity indices for each output component.

Each index is replaced by its absolute value divided by the largest index. Thus, the standardized indices belong to the interval \([0,1]\).

Parameters:: indices (dict[str, list[dict[str, ndarray]]]) – The indices to be standardized.
Returns:: The standardized indices.
Return type:: dict[str, list[dict[str, ndarray]]]

to_dataset()¶

Convert SensitivityAnalysis.indices into a Dataset.

Returns:: The sensitivity indices.
Return type:: Dataset

to_pickle(file_path)¶

Save the current sensitivity analysis on the disk.

Parameters:: file_path (str | Path) – The path to the file.
Return type:: None

DEFAULT_DRIVER = 'lhs'¶

dataset: IODataset¶: The dataset containing the discipline evaluations.

default_output: Iterable[str]¶: The default outputs of interest.

property indices: dict[str, dict[str, list[dict[str, ndarray]]]]¶

The sensitivity indices.

With the following structure:

{
    "method_name": {
        "output_name": [
            {
                "input_name": data_array,
            }
        ]
    }
}

property input_names: list[str]¶: The names of the inputs.

property main_indices: dict[str, list[dict[str, ndarray]]]¶

The main sensitivity indices.

With the following structure:

{
    "output_name": [
        {
            "input_name": data_array,
        }
    ]
}

property main_method: Method¶

The name of the main method.

One of the enum Sensitivity.Method.

max: dict[str, dict[str, ndarray]]¶

The maximum effect with the following structure:

{
    "output_name": [
        {
            "input_name": data_array,
        }
    ]
}

min: dict[str, dict[str, ndarray]]¶

The minimum effect with the following structure:

{
    "output_name": [
        {
            "input_name": data_array,
        }
    ]
}

mu_: dict[str, dict[str, ndarray]]¶

The mean effects with the following structure:

{
    "output_name": [
        {
            "input_name": data_array,
        }
    ]
}

mu_star: dict[str, dict[str, ndarray]]¶

The mean absolute effects with the following structure:

{
    "output_name": [
        {
            "input_name": data_array,
        }
    ]
}

property n_replicates: int¶: The number of OAT replicates.

property outputs_bounds: dict[str, list[float]]¶: The empirical bounds of the outputs.

relative_sigma: dict[str, dict[str, ndarray]]¶

The relative variability of the effects with the following structure:

{
    "output_name": [
        {
            "input_name": data_array,
        }
    ]
}

sigma: dict[str, dict[str, ndarray]]¶

The variability of the effects with the following structure:

{
    "output_name": [
        {
            "input_name": data_array,
        }
    ]
}

Examples using MorrisAnalysis¶

Comparing sensitivity indices

Morris analysis