analytic module¶
A discipline based on analytic expressions.
- class gemseo.disciplines.analytic.AnalyticDiscipline(expressions, name=None, fast_evaluation=True, grammar_type=GrammarType.JSON)[source]
Bases:
MDODisciplineA discipline based on analytic expressions.
Use SymPy, a symbolic calculation engine.
Compute the Jacobian matrices by automatically differentiating the expressions.
Examples
>>> from gemseo.disciplines.analytic import AnalyticDiscipline >>> discipline = AnalyticDiscipline({"y_1": "2*x**2", "y_2": "4*x**2+5+z**3"})
Initialize self. See help(type(self)) for accurate signature.
- Parameters:
expressions (Mapping[str, str | Expr]) – The outputs expressed as functions of the inputs.
name (str | None) – The name of the discipline. If
None, use the class name.fast_evaluation (bool) –
Whether to apply
sympy.lambdifyto the expressions in order to accelerate their numerical evaluation; otherwise the expressions are evaluated withsympy.Expr.evalf.By default it is set to True.
grammar_type (MDODiscipline.GrammarType) –
The type of the input and output grammars.
By default it is set to “JSONGrammar”.
- cache: AbstractCache | None
The cache containing one or several executions of the discipline according to the cache policy.
- data_processor: DataProcessor
A tool to pre- and post-process discipline data.
- exec_for_lin: bool
Whether the last execution was due to a linearization.
- input_grammar: BaseGrammar
The input grammar.
- jac: MutableMapping[str, MutableMapping[str, ndarray | csr_array | JacobianOperator]]
The Jacobians of the outputs wrt inputs.
The structure is
{output: {input: matrix}}.
- name: str
The name of the discipline.
- output_grammar: BaseGrammar
The output grammar.
- output_names_to_symbols: dict[str, list[str]]
[‘in_1’, ‘in_2’]}``.
- Type:
The names of the inputs associated to the outputs, e.g. ``{‘out’
- re_exec_policy: ReExecutionPolicy
The policy to re-execute the same discipline.
- residual_variables: dict[str, str]
The output variables mapping to their inputs, to be considered as residuals; they shall be equal to zero.
- run_solves_residuals: bool
Whether the run method shall solve the residuals.
Examples using AnalyticDiscipline¶
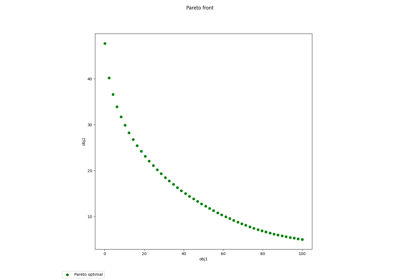
Pareto front on the Binh and Korn problem using a BiLevel formulation