Note
Click here to download the full example code
Sobol’ analysis¶
from __future__ import annotations
import pprint
from gemseo.uncertainty.sensitivity.sobol.analysis import SobolAnalysis
from gemseo.uncertainty.use_cases.ishigami.ishigami_discipline import IshigamiDiscipline
from gemseo.uncertainty.use_cases.ishigami.ishigami_space import IshigamiSpace
In this example, we consider the Ishigami function [IH90]
implemented as an MDODiscipline by the IshigamiDiscipline.
It is commonly used
with the independent random variables \(X_1\), \(X_2\) and \(X_3\)
uniformly distributed between \(-\pi\) and \(\pi\)
and defined in the IshigamiSpace.
discipline = IshigamiDiscipline()
uncertain_space = IshigamiSpace()
Then,
we run sensitivity analysis of type SobolAnalysis:
sensitivity_analysis = SobolAnalysis([discipline], uncertain_space, 10000)
sensitivity_analysis.main_method = "total"
sensitivity_analysis.compute_indices()
{'first': {'y': [{'x1': array([0.33668934]), 'x2': array([0.48974171]), 'x3': array([0.01387372])}]}, 'second': {'y': [{'x1': {'x1': array([[0.]]), 'x2': array([[-0.06556589]]), 'x3': array([[0.17784496]])}, 'x2': {'x1': array([[-0.06556589]]), 'x2': array([[0.]]), 'x3': array([[-0.05604046]])}, 'x3': {'x1': array([[0.17784496]]), 'x2': array([[-0.05604046]]), 'x3': array([[0.]])}}]}, 'total': {'y': [{'x1': array([0.49769038]), 'x2': array([0.46903493]), 'x3': array([0.23786094])}]}}
The resulting indices are the first-order and total Sobol’ indices:
pprint.pprint(sensitivity_analysis.indices)
{'first': {'y': [{'x1': array([0.33668934]),
'x2': array([0.48974171]),
'x3': array([0.01387372])}]},
'second': {'y': [{'x1': {'x1': array([[0.]]),
'x2': array([[-0.06556589]]),
'x3': array([[0.17784496]])},
'x2': {'x1': array([[-0.06556589]]),
'x2': array([[0.]]),
'x3': array([[-0.05604046]])},
'x3': {'x1': array([[0.17784496]]),
'x2': array([[-0.05604046]]),
'x3': array([[0.]])}}]},
'total': {'y': [{'x1': array([0.49769038]),
'x2': array([0.46903493]),
'x3': array([0.23786094])}]}}
They can also be accessed separately:
pprint.pprint(sensitivity_analysis.first_order_indices)
pprint.pprint(sensitivity_analysis.total_order_indices)
{'y': [{'x1': array([0.33668934]),
'x2': array([0.48974171]),
'x3': array([0.01387372])}]}
{'y': [{'x1': array([0.49769038]),
'x2': array([0.46903493]),
'x3': array([0.23786094])}]}
One can also obtain their confidence intervals:
pprint.pprint(sensitivity_analysis.get_intervals())
pprint.pprint(sensitivity_analysis.get_intervals(first_order=False))
{'y': [{'x1': (array([0.27106596]), array([0.40231271])),
'x2': (array([0.42038752]), array([0.55909591])),
'x3': (array([-0.06311772]), array([0.09086516]))}]}
{'y': [{'x1': (array([0.42529255]), array([0.57008822])),
'x2': (array([0.42022722]), array([0.51784263])),
'x3': (array([0.19308657]), array([0.2826353]))}]}
The main indices are the total Sobol’ indices
(SobolAnalysis.main_method can also be set to "first"
to use the first-order indices as main indices):
pprint.pprint(sensitivity_analysis.main_indices)
{'y': [{'x1': array([0.49769038]),
'x2': array([0.46903493]),
'x3': array([0.23786094])}]}
These main indices are used to sort the input parameters by decreasing order of influence:
print(sensitivity_analysis.sort_parameters("y"))
['x1', 'x2', 'x3']
Lastly,
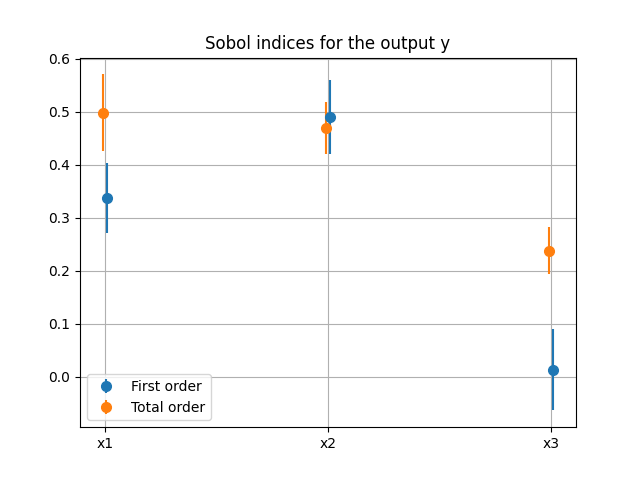
we can use the method SobolAnalysis.plot()
to visualize both first-order and total Sobol’ indices:
sensitivity_analysis.plot("y", save=False, show=True)
Total running time of the script: ( 0 minutes 15.799 seconds)
