mdo_scenario module¶
A scenario whose driver is an optimization algorithm.
- class gemseo.core.mdo_scenario.MDOScenario(disciplines, formulation, objective_name, design_space, name=None, grammar_type=GrammarType.JSON, maximize_objective=False, **formulation_options)[source]¶
Bases:
ScenarioA multidisciplinary scenario to be executed by an optimizer.
an
MDOScenariois a particularScenariowhose driver is an optimization algorithm. This algorithm must be implemented in anOptimizationLibrary.Initialize self. See help(type(self)) for accurate signature.
- Parameters:
disciplines (Sequence[MDODiscipline]) – The disciplines used to compute the objective, constraints and observables from the design variables.
formulation (str) – The class name of the
MDOFormulation, e.g."MDF","IDF"or"BiLevel".objective_name (str | Sequence[str]) – The name(s) of the discipline output(s) used as objective. If multiple names are passed, the objective will be a vector.
design_space (DesignSpace) – The search space including at least the design variables (some formulations requires additional variables, e.g.
IDFwith the coupling variables).name (str | None) – The name to be given to this scenario. If
None, use the name of the class.grammar_type (MDODiscipline.GrammarType) –
The grammar for the scenario and the MDO formulation.
By default it is set to “JSONGrammar”.
maximize_objective (bool) –
Whether to maximize the objective.
By default it is set to False.
**formulation_options (Any) – The options of the
MDOFormulation.
- class ApproximationMode(value)¶
Bases:
StrEnumThe approximation derivation modes.
- CENTERED_DIFFERENCES = 'centered_differences'¶
The centered differences method used to approximate the Jacobians by perturbing each variable with a small real number.
- COMPLEX_STEP = 'complex_step'¶
The complex step method used to approximate the Jacobians by perturbing each variable with a small complex number.
- FINITE_DIFFERENCES = 'finite_differences'¶
The finite differences method used to approximate the Jacobians by perturbing each variable with a small real number.
- class CacheType(value)¶
Bases:
StrEnumThe name of the cache class.
- HDF5 = 'HDF5Cache'¶
- MEMORY_FULL = 'MemoryFullCache'¶
- NONE = ''¶
No cache is used.
- SIMPLE = 'SimpleCache'¶
- class DifferentiationMethod(value)¶
Bases:
StrEnumThe differentiation methods.
- CENTERED_DIFFERENCES = 'centered_differences'¶
- COMPLEX_STEP = 'complex_step'¶
- FINITE_DIFFERENCES = 'finite_differences'¶
- NO_DERIVATIVE = 'no_derivative'¶
- USER_GRAD = 'user'¶
- class ExecutionStatus(value)¶
Bases:
StrEnumThe execution statuses of a discipline.
- DONE = 'DONE'¶
- FAILED = 'FAILED'¶
- LINEARIZE = 'LINEARIZE'¶
- PENDING = 'PENDING'¶
- RUNNING = 'RUNNING'¶
- VIRTUAL = 'VIRTUAL'¶
- class GrammarType(value)¶
Bases:
StrEnumThe name of the grammar class.
- JSON = 'JSONGrammar'¶
- PYDANTIC = 'PydanticGrammar'¶
- SIMPLE = 'SimpleGrammar'¶
- SIMPLER = 'SimplerGrammar'¶
- class InitJacobianType(value)¶
Bases:
StrEnumThe way to initialize Jacobian matrices.
- DENSE = 'dense'¶
The Jacobian is initialized as a NumPy ndarray filled in with zeros.
- EMPTY = 'empty'¶
The Jacobian is initialized as an empty NumPy ndarray.
- SPARSE = 'sparse'¶
The Jacobian is initialized as a SciPy CSR array with zero elements.
- class LinearizationMode(value)¶
Bases:
StrEnumAn enumeration.
- ADJOINT = 'adjoint'¶
- AUTO = 'auto'¶
- CENTERED_DIFFERENCES = 'centered_differences'¶
- COMPLEX_STEP = 'complex_step'¶
- DIRECT = 'direct'¶
- FINITE_DIFFERENCES = 'finite_differences'¶
- REVERSE = 'reverse'¶
- class ReExecutionPolicy(value)¶
Bases:
StrEnumThe re-execution policy of a discipline.
- DONE = 'RE_EXEC_DONE'¶
- NEVER = 'RE_EXEC_NEVER'¶
- classmethod activate_time_stamps()¶
Activate the time stamps.
For storing start and end times of execution and linearizations.
- Return type:
None
- add_constraint(output_name, constraint_type=ConstraintType.EQ, constraint_name=None, value=None, positive=False, **kwargs)¶
Add a design constraint.
This constraint is in addition to those created by the formulation, e.g. consistency constraints in IDF.
The strategy of repartition of the constraints is defined by the formulation.
- Parameters:
output_name (str | Sequence[str]) – The names of the outputs to be used as constraints. For instance, if “g_1” is given and constraint_type=”eq”, g_1=0 will be added as constraint to the optimizer. If several names are given, a single discipline must provide all outputs.
constraint_type (MDOFunction.ConstraintType) –
The type of constraint.
By default it is set to “eq”.
constraint_name (str | None) – The name of the constraint to be stored. If
None, the name of the constraint is generated from the output name.value (float | None) – The value for which the constraint is active. If
None, this value is 0.positive (bool) –
If
True, the inequality constraint is positive.By default it is set to False.
- Raises:
ValueError – If the constraint type is neither ‘eq’ nor ‘ineq’.
- Return type:
None
- add_differentiated_inputs(inputs=None)¶
Add the inputs for differentiation.
The inputs that do not represent continuous numbers are filtered out.
- Parameters:
inputs (Iterable[str] | None) – The input variables against which to differentiate the outputs. If
None, all the inputs of the discipline are used.- Raises:
ValueError – When ``inputs `` are not in the input grammar.
- Return type:
None
- add_differentiated_outputs(outputs=None)¶
Add the outputs for differentiation.
The outputs that do not represent continuous numbers are filtered out.
- Parameters:
outputs (Iterable[str] | None) – The output variables to be differentiated. If
None, all the outputs of the discipline are used.- Raises:
ValueError – When ``outputs `` are not in the output grammar.
- Return type:
None
- add_namespace_to_input(name, namespace)¶
Add a namespace prefix to an existing input grammar element.
The updated input grammar element name will be
namespace+namespaces_separator+name.
- add_namespace_to_output(name, namespace)¶
Add a namespace prefix to an existing output grammar element.
The updated output grammar element name will be
namespace+namespaces_separator+name.
- add_observable(output_names, observable_name=None, discipline=None)¶
Add an observable to the optimization problem.
The repartition strategy of the observable is defined in the formulation class. When more than one output name is provided, the observable function returns a concatenated array of the output values.
- Parameters:
output_names (Sequence[str]) – The names of the outputs to observe.
observable_name (Sequence[str] | None) – The name to be given to the observable. If
None, the output name is used by default.discipline (MDODiscipline | None) – The discipline used to build the observable function. If
None, detect the discipline from the inner disciplines.
- Return type:
None
- add_status_observer(obs)¶
Add an observer for the status.
Add an observer for the status to be notified when self changes of status.
- Parameters:
obs (Any) – The observer to add.
- Return type:
None
- auto_get_grammar_file(is_input=True, name=None, comp_dir=None)¶
Use a naming convention to associate a grammar file to the discipline.
Search in the directory
comp_dirfor either an input grammar file namedname + "_input.json"or an output grammar file namedname + "_output.json".- Parameters:
is_input (bool) –
Whether to search for an input or output grammar file.
By default it is set to True.
name (str | None) – The name to be searched in the file names. If
None, use the name of the discipline class.comp_dir (str | Path | None) – The directory in which to search the grammar file. If
None, use theGRAMMAR_DIRECTORYif any, or the directory of the discipline class module.
- Returns:
The grammar file path.
- Return type:
Path
- check_input_data(input_data, raise_exception=True)¶
Check the input data validity.
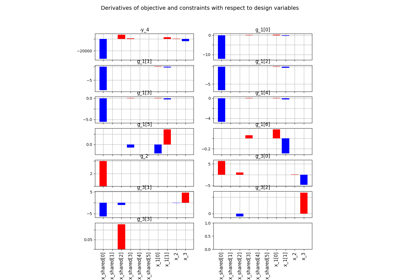
- check_jacobian(input_data=None, derr_approx=ApproximationMode.FINITE_DIFFERENCES, step=1e-07, threshold=1e-08, linearization_mode='auto', inputs=None, outputs=None, parallel=False, n_processes=2, use_threading=False, wait_time_between_fork=0, auto_set_step=False, plot_result=False, file_path='jacobian_errors.pdf', show=False, fig_size_x=10, fig_size_y=10, reference_jacobian_path=None, save_reference_jacobian=False, indices=None)¶
Check if the analytical Jacobian is correct with respect to a reference one.
If reference_jacobian_path is not None and save_reference_jacobian is True, compute the reference Jacobian with the approximation method and save it in reference_jacobian_path.
If reference_jacobian_path is not None and save_reference_jacobian is False, do not compute the reference Jacobian but read it from reference_jacobian_path.
If reference_jacobian_path is None, compute the reference Jacobian without saving it.
- Parameters:
input_data (Mapping[str, ndarray] | None) – The input data needed to execute the discipline according to the discipline input grammar. If
None, use theMDODiscipline.default_inputs.derr_approx (ApproximationMode) –
The approximation method, either “complex_step” or “finite_differences”.
By default it is set to “finite_differences”.
threshold (float) –
The acceptance threshold for the Jacobian error.
By default it is set to 1e-08.
linearization_mode (str) –
the mode of linearization: direct, adjoint or automated switch depending on dimensions of inputs and outputs (Default value = ‘auto’)
By default it is set to “auto”.
inputs (Iterable[str] | None) – The names of the inputs wrt which to differentiate the outputs.
outputs (Iterable[str] | None) – The names of the outputs to be differentiated.
step (float) –
The differentiation step.
By default it is set to 1e-07.
parallel (bool) –
Whether to differentiate the discipline in parallel.
By default it is set to False.
n_processes (int) –
The maximum simultaneous number of threads, if
use_threadingis True, or processes otherwise, used to parallelize the execution.By default it is set to 2.
use_threading (bool) –
Whether to use threads instead of processes to parallelize the execution; multiprocessing will copy (serialize) all the disciplines, while threading will share all the memory This is important to note if you want to execute the same discipline multiple times, you shall use multiprocessing.
By default it is set to False.
wait_time_between_fork (float) –
The time waited between two forks of the process / thread.
By default it is set to 0.
auto_set_step (bool) –
Whether to compute the optimal step for a forward first order finite differences gradient approximation.
By default it is set to False.
plot_result (bool) –
Whether to plot the result of the validation (computed vs approximated Jacobians).
By default it is set to False.
file_path (str | Path) –
The path to the output file if
plot_resultisTrue.By default it is set to “jacobian_errors.pdf”.
show (bool) –
Whether to open the figure.
By default it is set to False.
fig_size_x (float) –
The x-size of the figure in inches.
By default it is set to 10.
fig_size_y (float) –
The y-size of the figure in inches.
By default it is set to 10.
reference_jacobian_path (str | Path | None) – The path of the reference Jacobian file.
save_reference_jacobian (bool) –
Whether to save the reference Jacobian.
By default it is set to False.
indices (Iterable[int] | None) – The indices of the inputs and outputs for the different sub-Jacobian matrices, formatted as
{variable_name: variable_components}wherevariable_componentscan be either an integer, e.g. 2 a sequence of integers, e.g. [0, 3], a slice, e.g. slice(0,3), the ellipsis symbol (…) or None, which is the same as ellipsis. If a variable name is missing, consider all its components. IfNone, consider all the components of all theinputsandoutputs.
- Returns:
Whether the analytical Jacobian is correct with respect to the reference one.
- Return type:
- check_output_data(raise_exception=True)¶
Check the output data validity.
- Parameters:
raise_exception (bool) –
Whether to raise an exception when the data is invalid.
By default it is set to True.
- Return type:
None
- classmethod deactivate_time_stamps()¶
Deactivate the time stamps.
For storing start and end times of execution and linearizations.
- Return type:
None
- execute(input_data=None)¶
Execute the discipline.
This method executes the discipline:
Adds the default inputs to the
input_dataif some inputs are not defined in input_data but exist inMDODiscipline.default_inputs.Checks whether the last execution of the discipline was called with identical inputs, i.e. cached in
MDODiscipline.cache; if so, directly returnsself.cache.get_output_cache(inputs).Caches the inputs.
Checks the input data against
MDODiscipline.input_grammar.If
MDODiscipline.data_processoris not None, runs the preprocessor.Updates the status to
MDODiscipline.ExecutionStatus.RUNNING.Calls the
MDODiscipline._run()method, that shall be defined.If
MDODiscipline.data_processoris not None, runs the postprocessor.Checks the output data.
Caches the outputs.
Updates the status to
MDODiscipline.ExecutionStatus.DONEorMDODiscipline.ExecutionStatus.FAILED.Updates summed execution time.
- Parameters:
input_data (Mapping[str, Any] | None) – The input data needed to execute the discipline according to the discipline input grammar. If
None, use theMDODiscipline.default_inputs.- Returns:
The discipline local data after execution.
- Return type:
- static from_pickle(file_path)¶
Deserialize a discipline from a file.
- Parameters:
file_path (str | Path) – The path to the file containing the discipline.
- Returns:
The discipline instance.
- Return type:
- get_all_inputs()¶
Return the local input data.
The order is given by
MDODiscipline.get_input_data_names().- Returns:
The local input data.
- Return type:
Iterator[Any]
- get_all_outputs()¶
Return the local output data.
The order is given by
MDODiscipline.get_output_data_names().- Returns:
The local output data.
- Return type:
Iterator[Any]
- static get_data_list_from_dict(keys, data_dict)¶
Filter the dict from a list of keys or a single key.
If keys is a string, then the method return the value associated to the key. If keys is a list of strings, then the method returns a generator of value corresponding to the keys which can be iterated.
- get_disciplines_in_dataflow_chain()¶
Return the disciplines that must be shown as blocks in the XDSM.
By default, only the discipline itself is shown. This function can be differently implemented for any type of inherited discipline.
- Returns:
The disciplines shown in the XDSM chain.
- Return type:
- get_disciplines_statuses()¶
Retrieve the statuses of the disciplines.
- get_expected_dataflow()¶
Return the expected data exchange sequence.
This method is used for the XDSM representation.
The default expected data exchange sequence is an empty list.
See also
MDOFormulation.get_expected_dataflow
- Returns:
The data exchange arcs.
- Return type:
- get_expected_workflow()¶
Return the expected execution sequence.
This method is used for the XDSM representation.
The default expected execution sequence is the execution of the discipline itself.
See also
MDOFormulation.get_expected_workflow
- Returns:
The expected execution sequence.
- Return type:
- get_input_data(with_namespaces=True)¶
Return the local input data as a dictionary.
- get_input_data_names(with_namespaces=True)¶
Return the names of the input variables.
- get_input_output_data_names(with_namespaces=True)¶
Return the names of the input and output variables.
- get_inputs_asarray()¶
Return the local output data as a large NumPy array.
The order is the one of
MDODiscipline.get_all_outputs().- Returns:
The local output data.
- Return type:
- get_inputs_by_name(data_names)¶
Return the local data associated with input variables.
- Parameters:
data_names (Iterable[str]) – The names of the input variables.
- Returns:
The local data for the given input variables.
- Raises:
ValueError – When a variable is not an input of the discipline.
- Return type:
Iterator[Any]
- get_local_data_by_name(data_names)¶
Return the local data of the discipline associated with variables names.
- Parameters:
data_names (Iterable[str]) – The names of the variables.
- Returns:
The local data associated with the variables names.
- Raises:
ValueError – When a name is not a discipline input name.
- Return type:
Iterator[Any]
- get_optim_variable_names()¶
A convenience function to access the optimization variables.
- get_output_data(with_namespaces=True)¶
Return the local output data as a dictionary.
- get_output_data_names(with_namespaces=True)¶
Return the names of the output variables.
- get_outputs_asarray()¶
Return the local input data as a large NumPy array.
The order is the one of
MDODiscipline.get_all_inputs().- Returns:
The local input data.
- Return type:
- get_outputs_by_name(data_names)¶
Return the local data associated with output variables.
- Parameters:
data_names (Iterable[str]) – The names of the output variables.
- Returns:
The local data for the given output variables.
- Raises:
ValueError – When a variable is not an output of the discipline.
- Return type:
Iterator[Any]
- get_result(name='', **options)¶
Return the result of the scenario execution.
- Parameters:
name (str) –
The class name of the
ScenarioResult. If empty, use a default one (seecreate_scenario_result()).By default it is set to “”.
**options (Any) – The options of the
ScenarioResult.
- Returns:
The result of the scenario execution.
- Return type:
- get_sub_disciplines(recursive=False)¶
Determine the sub-disciplines.
This method lists the sub-disciplines’ disciplines. It will list up to one level of disciplines contained inside another one unless the
recursiveargument is set toTrue.- Parameters:
recursive (bool) –
If
True, the method will look inside any discipline that has other disciplines inside until it reaches a discipline without sub-disciplines, in this case the return value will not include any discipline that has sub-disciplines. IfFalse, the method will list up to one level of disciplines contained inside another one, in this case the return value may include disciplines that contain sub-disciplines.By default it is set to False.
- Returns:
The sub-disciplines.
- Return type:
- is_all_inputs_existing(data_names)¶
Test if several variables are discipline inputs.
- is_all_outputs_existing(data_names)¶
Test if several variables are discipline outputs.
- is_input_existing(data_name)¶
Test if a variable is a discipline input.
- is_output_existing(data_name)¶
Test if a variable is a discipline output.
- linearize(input_data=None, compute_all_jacobians=False, execute=True)¶
Compute the Jacobians of some outputs with respect to some inputs.
- Parameters:
input_data (Mapping[str, Any] | None) – The input data for which to compute the Jacobian. If
None, use theMDODiscipline.default_inputs.compute_all_jacobians (bool) –
Whether to compute the Jacobians of all the output with respect to all the inputs. Otherwise, set the input variables against which to differentiate the output ones with
add_differentiated_inputs()and set these output variables to differentiate withadd_differentiated_outputs().By default it is set to False.
execute (bool) –
Whether to start by executing the discipline with the input data for which to compute the Jacobian; this allows to ensure that the discipline was executed with the right input data; it can be almost free if the corresponding output data have been stored in the
cache.By default it is set to True.
- Returns:
The Jacobian of the discipline shaped as
{output_name: {input_name: jacobian_array}}wherejacobian_array[i, j]is the partial derivative ofoutput_name[i]with respect toinput_name[j].- Raises:
ValueError – When either the inputs for which to differentiate the outputs or the outputs to differentiate are missing.
- Return type:
- notify_status_observers()¶
Notify all status observers that the status has changed.
- Return type:
None
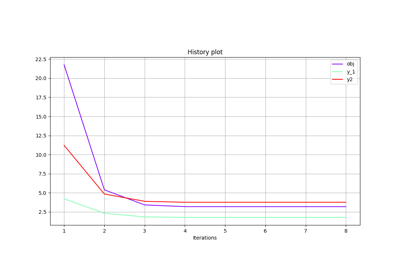
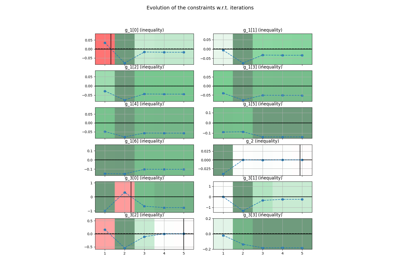
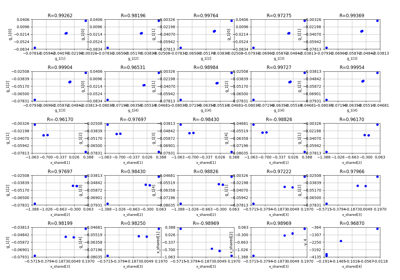
- post_process(post_name, **options)¶
Post-process the optimization history.
- Parameters:
post_name (str) – The name of the post-processor, i.e. the name of a class inheriting from
OptPostProcessor.**options (OptPostProcessorOptionType | Path) – The options for the post-processor.
- Returns:
The post-processing instance related to the optimization scenario.
- Return type:
- print_execution_metrics()¶
Print the total number of executions and cumulated runtime by discipline.
- Return type:
None
- remove_status_observer(obs)¶
Remove an observer for the status.
- Parameters:
obs (Any) – The observer to remove.
- Return type:
None
- reset_statuses_for_run()¶
Set all the statuses to
MDODiscipline.ExecutionStatus.PENDING.- Raises:
ValueError – When the discipline cannot be run because of its status.
- Return type:
None
- save_optimization_history(file_path, file_format='hdf5', append=False)¶
Save the optimization history of the scenario to a file.
- Parameters:
- Raises:
ValueError – If the file format is not correct.
- Return type:
None
- set_cache_policy(cache_type=CacheType.SIMPLE, cache_tolerance=0.0, cache_hdf_file=None, cache_hdf_node_path=None, is_memory_shared=True)¶
Set the type of cache to use and the tolerance level.
This method defines when the output data have to be cached according to the distance between the corresponding input data and the input data already cached for which output data are also cached.
The cache can be either a
SimpleCacherecording the last execution or a cache storing all executions, e.g.MemoryFullCacheandHDF5Cache. Caching data can be either in-memory, e.g.SimpleCacheandMemoryFullCache, or on the disk, e.g.HDF5Cache.The attribute
CacheFactory.cachesprovides the available caches types.- Parameters:
cache_type (CacheType) –
The type of cache.
By default it is set to “SimpleCache”.
cache_tolerance (float) –
The maximum relative norm of the difference between two input arrays to consider that two input arrays are equal.
By default it is set to 0.0.
cache_hdf_file (str | Path | None) – The path to the HDF file to store the data; this argument is mandatory when the
MDODiscipline.CacheType.HDF5policy is used.cache_hdf_node_path (str | None) – The name of the HDF file node to store the discipline data, possibly passed as a path
root_name/.../group_name/.../node_name. IfNone,MDODiscipline.nameis used.is_memory_shared (bool) –
Whether to store the data with a shared memory dictionary, which makes the cache compatible with multiprocessing.
By default it is set to True.
- Return type:
None
- set_differentiation_method(method=DifferentiationMethod.USER_GRAD, step=1e-06, cast_default_inputs_to_complex=False)¶
Set the differentiation method for the process.
When the selected method to differentiate the process is
complex_steptheDesignSpacecurrent value will be cast tocomplex128; additionally, if the optioncast_default_inputs_to_complexisTrue, the default inputs of the scenario’s disciplines will be cast as well provided that they arendarraywithdtypefloat64.- Parameters:
method (DifferentiationMethod) –
The method to use to differentiate the process.
By default it is set to “user”.
step (float) –
The finite difference step.
By default it is set to 1e-06.
cast_default_inputs_to_complex (bool) –
Whether to cast all float default inputs of the scenario’s disciplines if the selected method is
"complex_step".By default it is set to False.
- Return type:
None
- set_disciplines_statuses(status)¶
Set the sub-disciplines statuses.
To be implemented in subclasses.
- Parameters:
status (str) – The status.
- Return type:
None
- set_jacobian_approximation(jac_approx_type=ApproximationMode.FINITE_DIFFERENCES, jax_approx_step=1e-07, jac_approx_n_processes=1, jac_approx_use_threading=False, jac_approx_wait_time=0)¶
Set the Jacobian approximation method.
Sets the linearization mode to approx_method, sets the parameters of the approximation for further use when calling
MDODiscipline.linearize().- Parameters:
jac_approx_type (ApproximationMode) –
The approximation method, either “complex_step” or “finite_differences”.
By default it is set to “finite_differences”.
jax_approx_step (float) –
The differentiation step.
By default it is set to 1e-07.
jac_approx_n_processes (int) –
The maximum simultaneous number of threads, if
jac_approx_use_threadingis True, or processes otherwise, used to parallelize the execution.By default it is set to 1.
jac_approx_use_threading (bool) –
Whether to use threads instead of processes to parallelize the execution; multiprocessing will copy (serialize) all the disciplines, while threading will share all the memory This is important to note if you want to execute the same discipline multiple times, you shall use multiprocessing.
By default it is set to False.
jac_approx_wait_time (float) –
The time waited between two forks of the process / thread.
By default it is set to 0.
- Return type:
None
- set_linear_relationships(outputs=(), inputs=())¶
Set linear relationships between discipline inputs and outputs.
- Parameters:
outputs (Iterable[str]) –
The discipline output(s) in a linear relation with the input(s). If empty, all discipline outputs are considered.
By default it is set to ().
inputs (Iterable[str]) –
The discipline input(s) in a linear relation with the output(s). If empty, all discipline inputs are considered.
By default it is set to ().
- Return type:
None
- set_optimal_fd_step(outputs=None, inputs=None, compute_all_jacobians=False, print_errors=False, numerical_error=2.220446049250313e-16)¶
Compute the optimal finite-difference step.
Compute the optimal step for a forward first order finite differences gradient approximation. Requires a first evaluation of the perturbed functions values. The optimal step is reached when the truncation error (cut in the Taylor development), and the numerical cancellation errors (round-off when doing f(x+step)-f(x)) are approximately equal.
Warning
This calls the discipline execution twice per input variables.
See also
https://en.wikipedia.org/wiki/Numerical_differentiation and “Numerical Algorithms and Digital Representation”, Knut Morken , Chapter 11, “Numerical Differentiation”
- Parameters:
inputs (Iterable[str] | None) – The inputs wrt which the outputs are linearized. If
None, use theMDODiscipline._differentiated_inputs.outputs (Iterable[str] | None) – The outputs to be linearized. If
None, use theMDODiscipline._differentiated_outputs.compute_all_jacobians (bool) –
Whether to compute the Jacobians of all the output with respect to all the inputs. Otherwise, set the input variables against which to differentiate the output ones with
add_differentiated_inputs()and set these output variables to differentiate withadd_differentiated_outputs().By default it is set to False.
print_errors (bool) –
Whether to display the estimated errors.
By default it is set to False.
numerical_error (float) –
The numerical error associated to the calculation of f. By default, this is the machine epsilon (appx 1e-16), but can be higher when the calculation of f requires a numerical resolution.
By default it is set to 2.220446049250313e-16.
- Returns:
The estimated errors of truncation and cancellation error.
- Raises:
ValueError – When the Jacobian approximation method has not been set.
- Return type:
ndarray
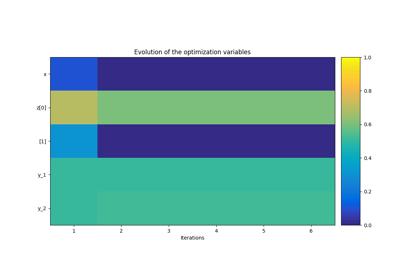
- set_optimization_history_backup(file_path, each_new_iter=False, each_store=True, erase=False, pre_load=False, generate_opt_plot=False)¶
Set the backup file for the optimization history during the run.
- Parameters:
file_path (str | Path) – The path to the file to save the history.
each_new_iter (bool) –
Whether the backup file is updated at every iteration of the optimization to store the database.
By default it is set to False.
each_store (bool) –
Whether the backup file is updated at every function call to store the database.
By default it is set to True.
erase (bool) –
Whether the backup file is erased before the run.
By default it is set to False.
pre_load (bool) –
Whether the backup file is loaded before run, useful after a crash.
By default it is set to False.
generate_opt_plot (bool) –
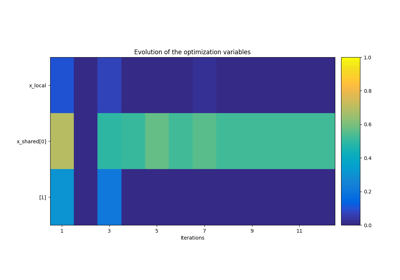
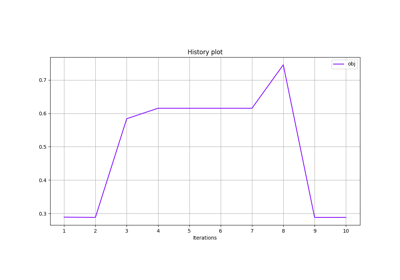
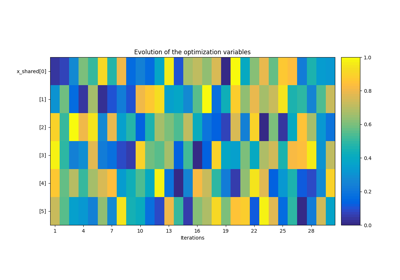
Whether to plot the optimization history view at each iteration. The plots will be generated only after the first two iterations.
By default it is set to False.
- Raises:
ValueError – If both
eraseandpre_loadareTrue.- Return type:
None
- store_local_data(**kwargs)¶
Store discipline data in local data.
- Parameters:
**kwargs (Any) – The data to be stored in
MDODiscipline.local_data.- Return type:
None
- to_dataset(name='', categorize=True, opt_naming=True, export_gradients=False)¶
Export the database of the optimization problem to a
Dataset.The variables can be classified into groups:
Dataset.DESIGN_GROUPorDataset.INPUT_GROUPfor the design variables andDataset.FUNCTION_GROUPorDataset.OUTPUT_GROUPfor the functions (objective, constraints and observables).- Parameters:
name (str) –
The name to be given to the dataset. If empty, use the name of the
OptimizationProblem.database.By default it is set to “”.
categorize (bool) –
Whether to distinguish between the different groups of variables. Otherwise, group all the variables in
Dataset.PARAMETER_GROUP`.By default it is set to True.
opt_naming (bool) –
Whether to use
Dataset.DESIGN_GROUPandDataset.FUNCTION_GROUPas groups. Otherwise, useDataset.INPUT_GROUPandDataset.OUTPUT_GROUP.By default it is set to True.
export_gradients (bool) –
Whether to export the gradients of the functions (objective function, constraints and observables) if the latter are available in the database of the optimization problem.
By default it is set to False.
- Returns:
A dataset built from the database of the optimization problem.
- Return type:
- to_pickle(file_path)¶
Serialize the discipline and store it in a file.
- Parameters:
file_path (str | Path) – The path to the file to store the discipline.
- Return type:
None
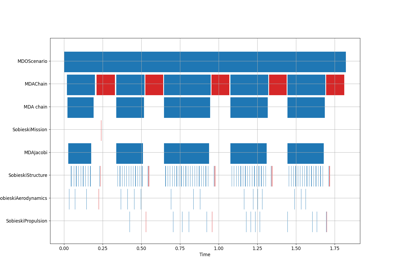
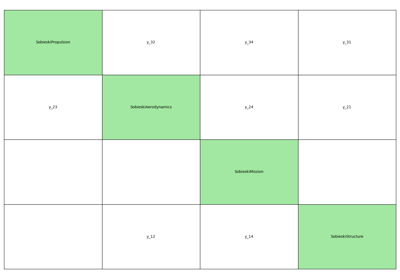
- xdsmize(monitor=False, directory_path='.', log_workflow_status=False, file_name='xdsm', show_html=False, save_html=True, save_json=False, save_pdf=False, pdf_build=True, pdf_cleanup=True, pdf_batchmode=True)¶
Create a XDSM diagram of the scenario.
- Parameters:
monitor (bool) –
Whether to update the generated file at each discipline status change.
By default it is set to False.
log_workflow_status (bool) –
Whether to log the evolution of the workflow’s status.
By default it is set to False.
directory_path (str | Path) –
The path of the directory to save the files. If
show_html=Trueandoutput_directory_path=None, the HTML file is stored in a temporary directory.By default it is set to “.”.
file_name (str) –
The file name without the file extension.
By default it is set to “xdsm”.
show_html (bool) –
Whether to open the web browser and display the XDSM.
By default it is set to False.
save_html (bool) –
Whether to save the XDSM as a HTML file.
By default it is set to True.
save_json (bool) –
Whether to save the XDSM as a JSON file.
By default it is set to False.
save_pdf (bool) –
Whether to save the XDSM as a PDF file.
By default it is set to False.
pdf_build (bool) –
Whether the standalone pdf of the XDSM will be built.
By default it is set to True.
pdf_cleanup (bool) –
Whether pdflatex built files will be cleaned up after build is complete.
By default it is set to True.
pdf_batchmode (bool) –
Whether pdflatex is run in batchmode.
By default it is set to True.
- Returns:
A view of the XDSM if
monitorisFalse.- Return type:
XDSM | None
- ALGO = 'algo'¶
- ALGO_OPTIONS = 'algo_options'¶
- GRAMMAR_DIRECTORY: ClassVar[str | None] = None¶
The directory in which to search for the grammar files if not the class one.
- L_BOUNDS = 'l_bounds'¶
- MAX_ITER = 'max_iter'¶
- U_BOUNDS = 'u_bounds'¶
- X_0 = 'x_0'¶
- X_OPT = 'x_opt'¶
- activate_counters: ClassVar[bool] = True¶
Whether to activate the counters (execution time, calls and linearizations).
- activate_input_data_check: ClassVar[bool] = True¶
Whether to check the input data respect the input grammar.
- activate_output_data_check: ClassVar[bool] = True¶
Whether to check the output data respect the output grammar.
- cache: AbstractCache | None¶
The cache containing one or several executions of the discipline according to the cache policy.
- property cache_tol: float¶
The cache input tolerance.
This is the tolerance for equality of the inputs in the cache. If norm(stored_input_data-input_data) <= cache_tol * norm(stored_input_data), the cached data for
stored_input_datais returned when callingself.execute(input_data).- Raises:
ValueError – When the discipline does not have a cache.
- data_processor: DataProcessor¶
A tool to pre- and post-process discipline data.
- property default_outputs: Defaults¶
The default outputs used when
virtual_executionisTrue.
- property design_space: DesignSpace¶
The design space on which the scenario is performed.
- property disciplines: list[MDODiscipline]¶
The sub-disciplines, if any.
- property exec_time: float | None¶
The cumulated execution time of the discipline.
This property is multiprocessing safe.
- Raises:
RuntimeError – When the discipline counters are disabled.
- formulation: MDOFormulation¶
The MDO formulation.
- property grammar_type: GrammarType¶
The type of grammar to be used for inputs and outputs declaration.
- input_grammar: BaseGrammar¶
The input grammar.
- jac: MutableMapping[str, MutableMapping[str, ndarray | csr_array | JacobianOperator]]¶
The Jacobians of the outputs wrt inputs.
The structure is
{output: {input: matrix}}.
- property linear_relationships: Mapping[str, Iterable[str]]¶
The linear relationships between inputs and outputs.
- property linearization_mode: LinearizationMode¶
The linearization mode among
MDODiscipline.LinearizationMode.- Raises:
ValueError – When the linearization mode is unknown.
- property local_data: DisciplineData¶
The current input and output data.
- property n_calls: int | None¶
The number of times the discipline was executed.
This property is multiprocessing safe.
- Raises:
RuntimeError – When the discipline counters are disabled.
- property n_calls_linearize: int | None¶
The number of times the discipline was linearized.
This property is multiprocessing safe.
- Raises:
RuntimeError – When the discipline counters are disabled.
- optimization_result: OptimizationResult | None¶
The optimization result if the scenario has been executed; otherwise
None.
- output_grammar: BaseGrammar¶
The output grammar.
- property post_factory: PostFactory¶
The factory of post-processors.
- re_exec_policy: ReExecutionPolicy¶
The policy to re-execute the same discipline.
- residual_variables: dict[str, str]¶
The output variables mapping to their inputs, to be considered as residuals; they shall be equal to zero.
- property status: ExecutionStatus¶
The status of the discipline.
The status aims at monitoring the process and give the user a simplified view on the state (the process state = execution or linearize or done) of the disciplines. The core part of the execution is _run, the core part of linearize is _compute_jacobian or approximate jacobian computation.
- time_stamps: ClassVar[dict[str, float] | None] = None¶
The mapping from discipline name to their execution time.
- property use_standardized_objective: bool¶
Whether to use the standardized objective for logging and post-processing.
The objective is
OptimizationProblem.objective.
- virtual_execution: ClassVar[bool] = False¶
Whether to skip the
_run()method during execution and return thedefault_outputs, whatever the inputs.
Examples using MDOScenario¶
Example for exterior penalty applied to the Sobieski test case.
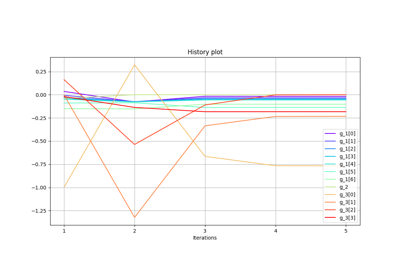
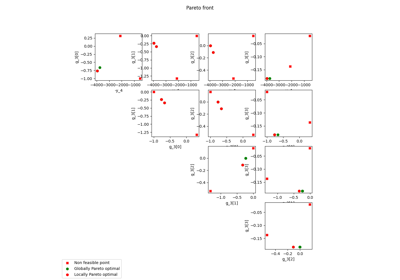
Pareto front on the Binh and Korn problem using a BiLevel formulation
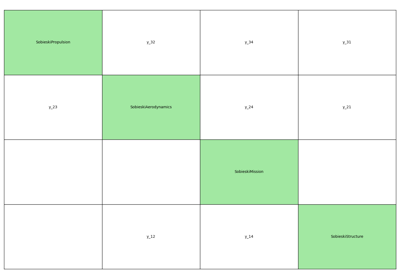
Application: Sobieski’s Super-Sonic Business Jet (MDO)
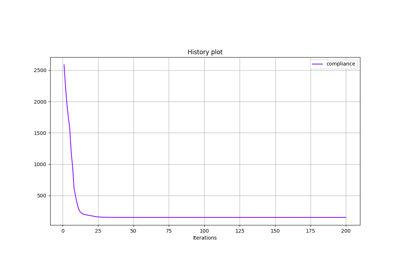
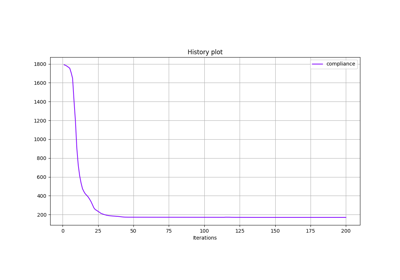
Solve a 2D short cantilever topology optimization problem